DP는 언제 풀어도 너무 어렵다 🥲
비트마스킹 + DP구조로 접근해야 한다는 것은 알았지만, 어떤 방식으로 DP배열을 초기화해야 할지 도무지 감이 안잡혔다
이분의 블로그를 참고하며... 설명이 정말 잘되어있어서 알고리즘을 잊지 않으려고 공부하고자 내식대로 다시 정리해봤다 ..!
https://withhamit.tistory.com/246
외판원 순회(TSP : Traveling Salesperson Probelm)
- 다수의 도시들이 있고, 어떤 도시 A에서 B로 이동할 때 드는 비용이 주어졌을 때, 어떤 도시에서 출발해서 모든 도시를 다 돈 후, 처음 출발했던 도시로 다시 돌아올 때 드는 최소 비용을 구하는 문제
- NP문제로 계산 이론에서 해를 구하기 어려운 문제의 대표적인 사례
문제 포인트
- 비트마스크를 통해 방문한 도시를 표현할 수 있음
- 출발 도시가 달라져도, 경로가 같으면 최소 비용이 같음
-
비트마스크를 통해 방문했던 경로를 어떻게 표현할까?
ex) 0~3번 도시가 있다고 하면 1101(2)는 0,2,3번 도시를 방문한 상태
1101(2)를 10진수 형태로 바꾸면 2^3+2^2+2^0=8+4+1=13(10)이다.
즉 이진수에서 0은 방문을 안한 도시이고, 1은 방문한 도시라고 할 수 있음. -
출발 도시가 달라진다면, 모든 도시를 순회하는 최소 비용이 달라질까?
결론부터 말하면, 달라지지 않는다.
어떤 도시에서 출발하든, 모든 도시를 돌고 다시 출발했던 도시로 돌아오는 과정에서 사이클이 발생하기 때문에 최소 비용은 같다.
예를 들어 (1->2->3, 2->3->1, 3->1->2는 모두 같은 경로라고 할 수 있다.)
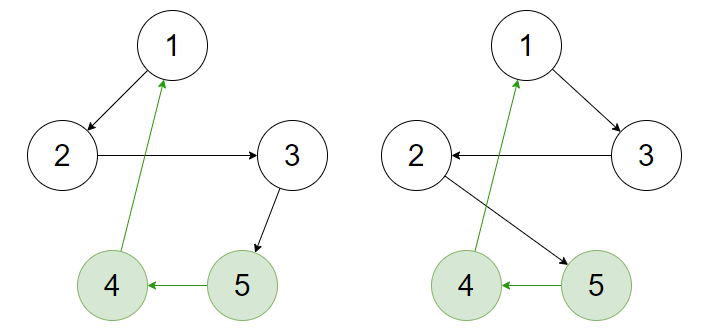
1에서 출발하는 경로를 위와 같은 예시로 들어보자. 왼쪽 경로를 먼저 계산하고, 오른쪽 경로를 계산한다고 하자.
왼쪽 : 1->2->3->5->4->1
오른쪽 : 1->3->2->5->4->1
5->4->1의 경로가 서로 중복됨.
이미 방문한 도시들과 현재 위치한 도시가 같은 경우 최소 비용이 같기 때문에, 왼쪽에서 먼저 같은 경로를 방문했다면 오른쪽에서는 이 경로를 일일이 방문하지 않고도 최소 비용을 구할 수 있다.
최소 비용을 저장하는 dp배열 구조는 다음과 같다.
- dp[curr][visit]
- curr : 현재 위치한 도시
- visit : 지금까지 방문한 도시들의 집합 (비트마스크)
- dp[curr][visit] : 방문하지 않은 나머지 도시(visit에 표시가 안된 도시)를 모두 방문한 뒤, 출발 도시까지 돌아갔을 때 드는 최소 비용
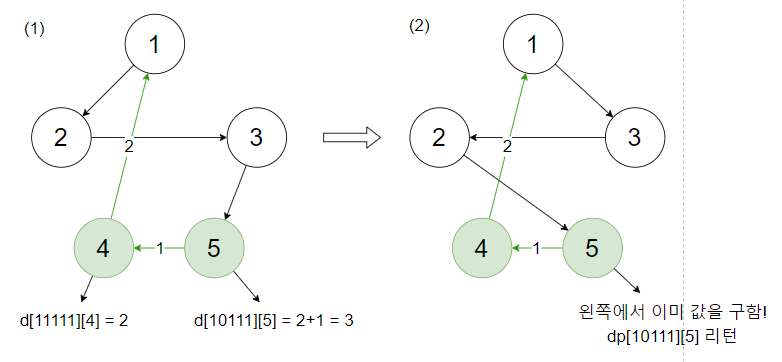
이를 다시 dp배열을 통해 설명하자면, 5->4->1의 경로에서 왼쪽에서 이미 dp[11111][4] (4->1까지의 비용), dp[10111][5]((5->4->1)까지의 비용)의 값을 먼저 구했기 때문에, 오른쪽에서 같은 경로를 지날때 dp[10111][5] 값을 리턴하면 된다.
위와같은 방식으로 어떤 출발 도시 A에서 다른 도시 B,C,D,...로 이동했을 때,
각 도시에서 방문한 도시들을 제외하고 남은 도시들을 지나 다시 출발 도시로 돌아왔을 때의 최소 비용들을 구하고,
이 값들 중 최소인 값이 정답이 된다.
코드
import java.io.*;
import java.util.*;
public class Main {
static int N;
static final int INF = 16_000_000;
static int[][] W, dp;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = null;
N = Integer.parseInt(br.readLine());
W = new int[N][N];
for(int i=0;i<N;i++) {
st = new StringTokenizer(br.readLine());
for(int j=0;j<N;j++) W[i][j] = Integer.parseInt(st.nextToken());
}
dp = new int[N][(1<<N)-1];
for(int i=0;i<N;i++) Arrays.fill(dp[i], -1);
bw.write(dfs(0, 1)+"\n");
bw.flush();
br.close();
}
static int dfs(int now, int visit) {
// 모든 도시를 지난 경우
if(visit == (1<<N)-1) {
// now -> 0(출발도시)로 가는 경로가 존재해야 돌아갈 수 있음
if(W[now][0] == 0) return INF;
return W[now][0];
}
if(dp[now][visit] != -1) return dp[now][visit];
dp[now][visit] = INF;
for(int i=0;i<N;i++) {
// now -> 아직 방문하지 않는 i번 도시 가는 경로가 있는 경우
if((visit & (1<<i)) == 0 && W[now][i] != 0) {
// d[i][j] = 현재 있는 도시가 i이고 이미 방문한 도시들의 집합이 j일때,
// 방문하지 않은 나머지 도시들을 모두 방문한 뒤 출발 도시로 돌아올 때 드는 최소 비용.
// 즉, 방문해야하는 도시(여기에 시작지점으로 돌아오는 것 포함) 들까지 가는 최소 비용
dp[now][visit] = Math.min(dfs(i, visit | (1 << i)) + W[now][i], dp[now][visit]); // 최소비용 갱신
// dfs(다음 도시, 다음도시 방문했다고 가정) + 여기서 다음 도시까지의 거리 와 최소거리 비교
}
}
return dp[now][visit];
}
}