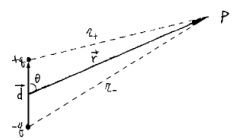
쌍극자(dipole)는 두 개의 반대 부호의 전하가 약간 떨어진 상태로 같이 있는 분포를 말한다. 이를테면 d d d + q +q + q − q -q − q
그러면 점 P P P
V ( r ⃗ ) = 1 4 π ε 0 ( q r + + − q r − ) = q 4 π ε 0 ( 1 r + − 1 r − ) V(\vec{r}) = \frac{1}{4\pi \varepsilon_0}\left(\frac{q}{r_+} + \frac{-q}{r_-} \right) = \frac{q}{4\pi \varepsilon_0}\left(\frac{1}{r_+} - \frac{1}{r_-} \right) V ( r ) = 4 π ε 0 1 ( r + q + r − − q ) = 4 π ε 0 q ( r + 1 − r − 1 ) 여기서 코사인 법칙에 의해
r + 2 = r 2 + ( d 2 ) 2 − 2 r ( d 2 ) cos θ r_+^2 = r^2 + \left(\frac{d}{2}\right)^2 - 2r\left(\frac{d}{2}\right)\cos\theta r + 2 = r 2 + ( 2 d ) 2 − 2 r ( 2 d ) cos θ 인데, 이를 이용하여 r ≫ d r\gg d r ≫ d
1 r + = 1 r ( 1 − d r cos θ + d 2 4 r 2 ) − 1 / 2 ≃ 1 r ( 1 + d 2 r cos θ ) , 1 r − = 1 r ( 1 + d r cos θ + d 2 4 r 2 ) − 1 / 2 ≃ 1 r ( 1 − d 2 r cos θ ) \begin{aligned} \frac{1}{r_+} &= \frac{1}{r}\left(1-\frac{d}{r}\cos\theta+\frac{d^2}{4r^2}\right)^{-1/2} \simeq \frac{1}{r}\left(1+\frac{d}{2r}\cos\theta\right)\,,\\ \frac{1}{r_-} &= \frac{1}{r}\left(1+\frac{d}{r}\cos\theta+\frac{d^2}{4r^2}\right)^{-1/2} \simeq \frac{1}{r}\left(1-\frac{d}{2r}\cos\theta\right)\\ \end{aligned} r + 1 r − 1 = r 1 ( 1 − r d cos θ + 4 r 2 d 2 ) − 1 / 2 ≃ r 1 ( 1 + 2 r d cos θ ) , = r 1 ( 1 + r d cos θ + 4 r 2 d 2 ) − 1 / 2 ≃ r 1 ( 1 − 2 r d cos θ ) 이므로
1 r + − 1 r − ≃ d cos θ r \frac{1}{r_+} - \frac{1}{r_-} \simeq \frac{d\cos\theta}{r} r + 1 − r − 1 ≃ r d cos θ 이 되어서 전기 퍼텐셜은
V ( r ⃗ ) = q 4 π ε 0 d cos θ r + ⋯ = 1 4 π ε 0 p ⃗ ⋅ r ^ r 2 + ⋯ V(\vec{r}) = \frac{q}{4\pi \varepsilon_0}\frac{d\cos\theta}{r} + \cdots= \frac{1}{4\pi \varepsilon_0} \frac{\vec{p}\cdot \hat{r}}{r^2} + \cdots V ( r ) = 4 π ε 0 q r d cos θ + ⋯ = 4 π ε 0 1 r 2 p ⋅ r ^ + ⋯ 이 된다. 여기서 p ⃗ = q d ⃗ = q ( r + ⃗ − r − ⃗ ) \vec{p} = q\vec{d} = q(\vec{r_+} - \vec{r_-}) p = q d = q ( r + − r − )
V dip ( r ⃗ ) = 1 4 π ε 0 p ⃗ ⋅ r ^ r 2 V_{\text{dip}}(\vec{r}) = \frac{1}{4\pi \varepsilon_0} \frac{\vec{p}\cdot \hat{r}}{r^2} V dip ( r ) = 4 π ε 0 1 r 2 p ⋅ r ^ 이다. 즉 단일 전하의 전기 퍼텐셜이 1 / r 1/r 1 / r 1 / r 2 1/r^2 1 / r 2
이런 식으로 계속 하면 다중 전하 분포에서 단일항 퍼텐셜 V mon V_{\text{mon}} V mon V dip V_{\text{dip}} V dip V quad V_{\text{quad}} V quad 1 / r 3 1/r^3 1 / r 3