선형 근사와 미분소

"미분 가능한" 함수 $y = f(x)$는 특정한 점 $x=x_0$에서 접선, 즉 기울기 $f'(x_0)$를 가진다. 특히 $y = f(x)$가 직선이라면 직선의 방정식은 정확하게

으로 쓸 수 있다. $y = f(x)$가 임의의 미분 가능한 곡선일 때, $x=x_0$ 근처에서는

로 근사(approximation)할 수 있을 것이다. 이것을 "표준 선형 근사(standard linear approximation)"라고 한다. 이때

를 $y = f(x)$에 대한 "선형화(linearization)" 혹은 "선형 근사" 라고 한다.

이를테면 실수 $k$에 대해서 $f(x) = (1+x)^k$인 함수가 있다고 하면 $f'(x) = k(1+x)^{k-1}$이므로 "$f(x)$의 $x=0$ 근처에서의 선형화"는

이다.

본래 $y = f(x)$의 미분을 뜻하는 라이프니츠 표기법 $f'(x) = \frac{dy}{dx}$에서 $\frac{dy}{dx}$는 분수나 비율을 뜻하는 것이 아니다. 이제 $\frac{dy}{dx}$가 존재한다면, $dx$와 $dy$를 독립적인 각각의 대상으로 생각하는 "표기법"을 정의해보자. 즉, $dx$와 $dy$라는 대상끼리의 비율 관계가 존재한다면 $\frac{dy}{dx}$는 $y = f(x)$에서의 미분 $f'(x)$이 존재한다는 식으로 생각할 수 있는 "대상"을 정의하자는 뜻이다. 이러한 대상을 "미분소(differential)"라고 한다. 보다 엄밀한 정의는 다음과 같다:

(Definition) $y=f(x)$이 미분 가능한 함수라고 가정하자. 변수 $x$에 대한 미소 변위를 뜻하는 미분소(differential) $dx$가 존재한다면, 미분소 $dy$는

로 정의된다.

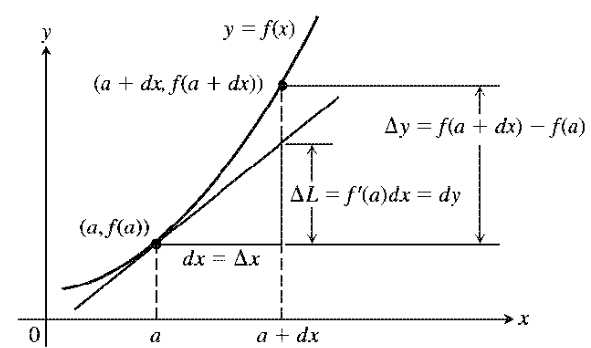
미분소의 기하학적인 의미는 위 그림에서의 $\Delta L$과 같다. $x=a$인 점을 생각하자. 그러면 $x$가 $a$에서 $a+dx$로 변화할 동안 $y=f(x)$의 변화는

이다. 이때 $x=a$에서의 접선 $y=L(x)$의 변화는 다음과 같다:

즉, $f(x)$의 선형화에서의 변화는 정확히 미분소 $dy$의 변화와 같다. 따라서 $dx \ne 0$이면 $dy$를 $dx$로 나눈 비율은 정확히 $f'(x)$와 같다.

이와 같은 방식으로 미분 가능한 함수 $f$의 미분소 $df$를

로 나타낼 수 있다.

(Theorem) (미분 가능성과 Error) $y=f(x)$가 $x=a$에서 미분 가능하고 $x$가 $a$에서 $a + \Delta x$까지 변한다고 가정하자. 그러면 $f$의 실제 변화 $\Delta f$는

로 나타낼 수 있다. 이때 $\Delta x \rightarrow 0$일 때 $\varepsilon \rightarrow 0$이다.

(증명) 만약 $f$가 $x=a$에서 미분 가능하고 $x$가 $a$에서 $a+\Delta x$로 변한다면 접선 $L(x)=f(a)+f'(a)(x-a)$에서의 변화는

이다. 즉, 이것은 $f$의 변화에 대한 미분 근사 $df=f'(a)\Delta x$와 동일하다. 한편 $f$의 실제 변화는

이다. 실제 변화와 미분 근사의 차이를 근사 오류(error)라고 해보자. 근사 오류를 구해보면

이다. 여기서 $\Delta x \rightarrow 0$일 때 $\frac{f(a+\Delta x)-f(a)}{\Delta x}$는 $f'(a)$에 가까워지므로 $\varepsilon \rightarrow 0$이 된다. 따라서 실제 변화 $\Delta f$는

로 쓸 수 있으며, 여기서 $\Delta x \rightarrow 0$일 때 $\varepsilon \rightarrow 0$이다. □