미분소와 연쇄 법칙
1.선형 근사와 미분소
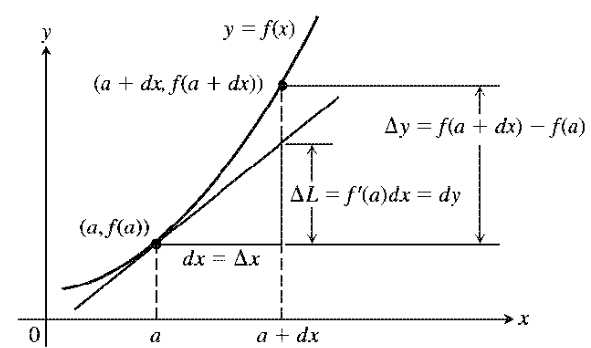
직선의 방정식은 $y = ax + b$이다. 또는 보다 일반적인 표현으로 임의의 직선은 $ax+bx+c=0$로 쓸 수 있다.이를 미분을 사용하여 표현해보자면, 모든 "미분 가능한" 곡선 $y = f(x)$은 임의의 $x=x_0$에서의 접선, 즉 기울기 $f'(x_0)$
2025년 1월 3일
2.연쇄 법칙 (Chain rule)

(Theorem) 만약 $f(u)$가 $u$에 대하여 미분 가능하고, $u=g(x)$이며 $g(x)$는 $x$에 대하여 미분 가능하다면 합성 함수 $(f\circ g)(x)=f(g(x))$는 $x$에 대하여 미분 가능하고, 이때 $$ (f\circ g)'(x)=f'(
2025년 1월 3일