2차원 평면 좌표계, 즉 R 2 \mathbb{R}^2 R 2 R 2 \mathbb{R}^2 R 2
(Definition) R 2 \mathbb{R}^2 R 2 f ( x , y ) f(x,y) f ( x , y ) ( x 0 , y 0 ) (x_0, y_0) ( x 0 , y 0 ) L L L f f f ε > 0 \varepsilon>0 ε > 0
0 < ( x − x 0 ) 2 + ( y − y 0 ) 2 < δ ⇒ ∣ f ( x ) − L ∣ < ε 0<\sqrt{(x-x_0)^2+(y-y_0)^2}<\delta \quad\Rightarrow\quad |f(x)-L|<\varepsilon 0 < ( x − x 0 ) 2 + ( y − y 0 ) 2 < δ ⇒ ∣ f ( x ) − L ∣ < ε 을 만족하는 적당한 δ > 0 \delta>0 δ > 0
lim ( x , y ) → ( x 0 , y 0 ) f ( x , y ) = L \lim_{(x,y)\rightarrow(x_0, y_0)}f(x,y)=L ( x , y ) → ( x 0 , y 0 ) lim f ( x , y ) = L 로 나타낸다.
2차원에서의 함수의 연속 역시 1차원 함수에서의 그것과 거의 유사하게 정의된다:
(Definition) 함수 f ( x , y ) f(x,y) f ( x , y )
f f f ( x 0 , y 0 ) (x_0, y_0) ( x 0 , y 0 ) lim ( x , y ) → ( x 0 , y 0 ) f ( x , y ) \lim_{(x,y)\rightarrow(x_0, y_0)}f(x,y) lim ( x , y ) → ( x 0 , y 0 ) f ( x , y ) lim ( x , y ) → ( x 0 , y 0 ) f ( x , y ) = f ( x 0 , y 0 ) \lim_{(x,y)\rightarrow(x_0, y_0)}f(x,y) = f(x_0,y_0) lim ( x , y ) → ( x 0 , y 0 ) f ( x , y ) = f ( x 0 , y 0 )
을 만족하면 "f f f ( x 0 , y 0 ) (x_0, y_0) ( x 0 , y 0 ) f f f f f f
이제 편미분을 정의하자:
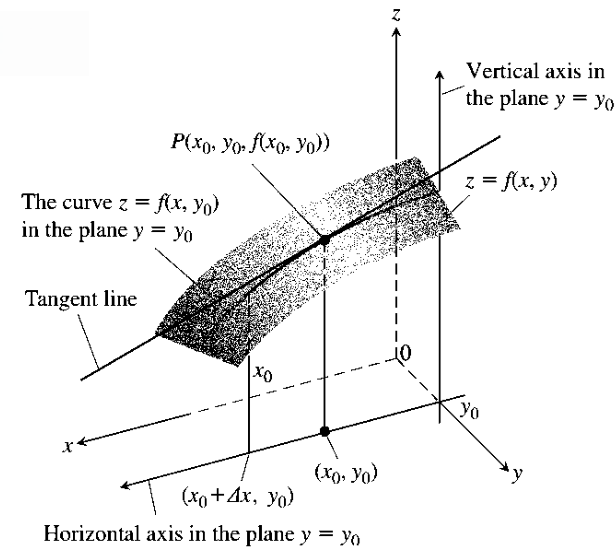
(Definition) 점 ( x 0 , y 0 ) (x_0, y_0) ( x 0 , y 0 ) f ( x , y ) f(x,y) f ( x , y ) x x x ∂ f / ∂ x \partial f / \partial x ∂ f / ∂ x
∂ f ∂ x ∣ ( x 0 , y 0 ) = lim Δ x → 0 f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) Δ x \left.\frac{\partial f}{\partial x}\right|_{(x_0, y_0)} =\lim_{\Delta x\rightarrow 0}\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x} ∂ x ∂ f ∣ ∣ ∣ ∣ ∣ ( x 0 , y 0 ) = Δ x → 0 lim Δ x f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) 으로 정의된다. 물론 해당 극한이 존재할 때 정의된다.
위 극한이 정의되는 상황을 그림으로 나타내면 다음과 같다:
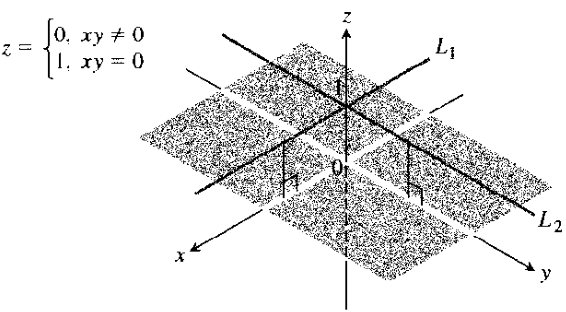
Ex. 다음 함수
f ( x , y ) = { 0 , x y ≠ 0 1 , x y = 0 f(x,y)=\begin{cases} 0\,,\, xy\ne 0 \\ 1\,,\, xy=0 \end{cases} f ( x , y ) = { 0 , x y = 0 1 , x y = 0 를 생각하자. 즉, 다음 그림과 같은 상황이다.y = x y=x y = x
lim ( x , y ) → ( x 0 , y 0 ) f ( x , y ) ∣ y = x lim ( x , y ) → ( x 0 , y 0 ) 0 = 0 . \left.\lim_{(x,y)\rightarrow(x_0, y_0)}f(x,y)\right|_{y=x} \lim_{(x,y)\rightarrow(x_0, y_0)}0 = 0\,. ( x , y ) → ( x 0 , y 0 ) lim f ( x , y ) ∣ ∣ ∣ ∣ ∣ y = x ( x , y ) → ( x 0 , y 0 ) lim 0 = 0 . 그런데 f ( 0 , 0 ) = 1 f(0,0)=1 f ( 0 , 0 ) = 1 f f f ( 0 , 0 ) (0,0) ( 0 , 0 ) ∂ f / ∂ x \partial f / \partial x ∂ f / ∂ x ∂ f / ∂ y \partial f / \partial y ∂ f / ∂ y ( 0 , 0 ) (0,0) ( 0 , 0 ) ( 0 , 0 ) (0,0) ( 0 , 0 ) ∂ f / ∂ x \partial f / \partial x ∂ f / ∂ x y = 0 y=0 y = 0 x x x f ( x , 0 ) = 1 f(x,0)=1 f ( x , 0 ) = 1 x x x ∂ f / ∂ x = 0 \partial f / \partial x=0 ∂ f / ∂ x = 0 ( 0 , 0 ) (0,0) ( 0 , 0 ) ∂ f / ∂ x = 0 \partial f / \partial x=0 ∂ f / ∂ x = 0 x = 0 x=0 x = 0 ( 0 , 0 ) (0,0) ( 0 , 0 ) ∂ f / ∂ y = 0 \partial f / \partial y=0 ∂ f / ∂ y = 0
위의 예제에도 불구하고, 여전히 2차원 이상의 고차원에서도 "미분 가능하면 연속"이 성립한다. 그러나 고차원에서는 "미분 가능"이 다르게 정의되며, 1차원보다 더 강력한 제약 조건이 따른다. 다음 글 에서 이에 대해 논의한다.