과적합을 해결하는 방법
과적합(overfitting)을 해결하는 방법으로는 크게 두가지가 있다.
- 특성의 갯수를 줄이기
주요특징을 직접 선택 or model selection algorithm 사용- 정규화를 수행하기
모든 특성을 사용, 하지만 파라미터의 값을 줄인다.
여기서 릿지 회귀가 바로 정규화를 위한 회귀모델이라고 할 수 있다. (정규화를 위한 회귀모델 중, Lidge 외에 Lasso, Elastic Net회귀모형 등이 있다.)
:
n: 샘플수, p: 특성수, : 튜닝 파라미터(패널티)
참고: alpha, lambda, regularization parameter, penalty term 모두 같은 뜻
위 식을 보면 OLS(최소제곱회귀) + 람다(λ)가 붙은 식으로 구성되어 있다!
이 람다값이 바로 튜닝 파라미터이다.
람다값을 조절함으로써 정규화를 수행할 수 있는 것이다.
우선 나는 수알못이기때문에 수식에 대해서는 이렇게만 이해하고 여기서 찾을 수 있는 람다값의 성질에 대해 말해보자.
람다값(λ)의 성질
→ 0, →
→ ∞, → 0.
람다값이 0이 된다면 어떻게 될까?
OLS와 같은 모양이 될 것이다. 아까 위의 식을 보면 더 쉽게 이해 할 수 있을 것이다.
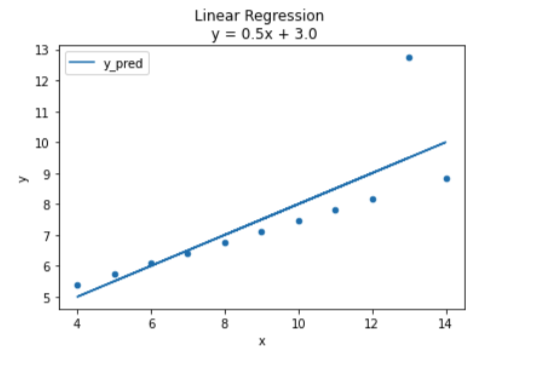
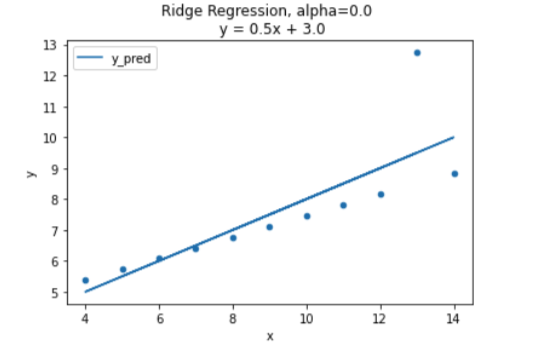
람다(알파)값이 0.0일때 OLS와 같은 그래프가 나왔다.
람다는 값이 커질루록 회귀계수들을 0으로 수렴시킨다. 이것은 덜 중요한 특성들을 0에 가깝게 수렴시켜 중요한 특성들이 비교적 돋보이게 해준다! 특성을 아예 없애버리진 않지만, 특성의 개수를 줄이는 효과를 냄으로써 과적합을 피할 수 있는 것이다. 다만 값이 너무 커져버린다면, 직선의 기울기가 0에 가까워지고 과소적합이 되어버린다. 아래의 그래프를 참고하자.
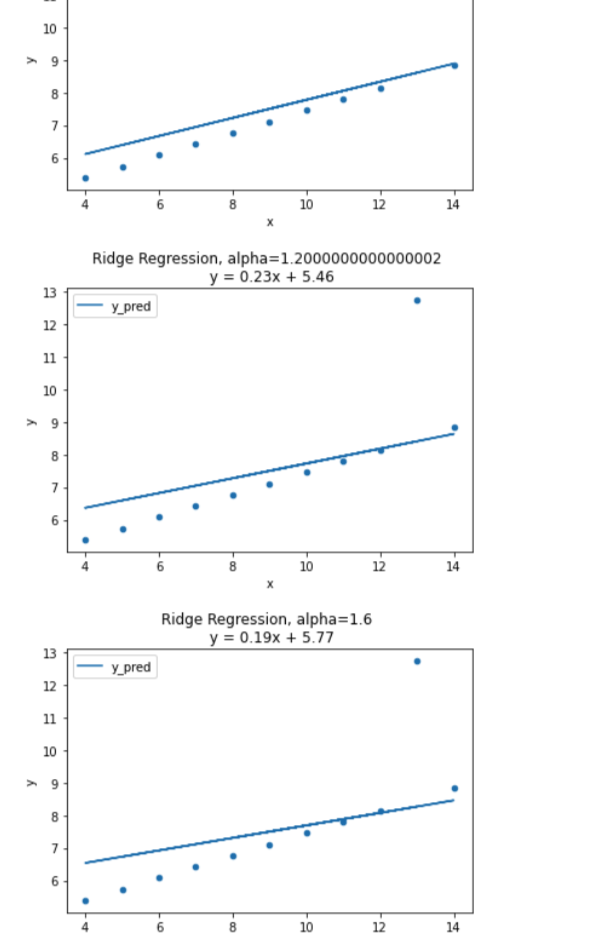
최적의 람다값(λ) 검증 - RidgeCV
그렇다면 최적의 람다(알파값)는 어떻게 찾아낼 수 있을까? -> 찾아내기 보다는,, 알파값을 입력하여 RidgeCV로 최적의 람다값을 검증 할 수 있다.
from sklearn.linear_model import RidgeCV
alphas = [0.01, 0.05, 0.1, 0.2, 1.0, 10.0, 100.0]
ridge = RidgeCV(alphas=alphas, normalize=True, cv=3)
ridge.fit(ans[['x']], ans['y'])
print("alpha: ", ridge.alpha_)
print("best score: ", ridge.best_score_)alpha: 0.2
best score: 0.4389766255562206다음은 최적의 람다값으로 그린 그래프이다. 다음 Ridge 회귀 직선의 생김새는 OLS와 매우 비슷하지만 이상치(outlier) 영향을 덜 받는다. 정규화에 어느정도 성공한 거라고 할 수 있다.
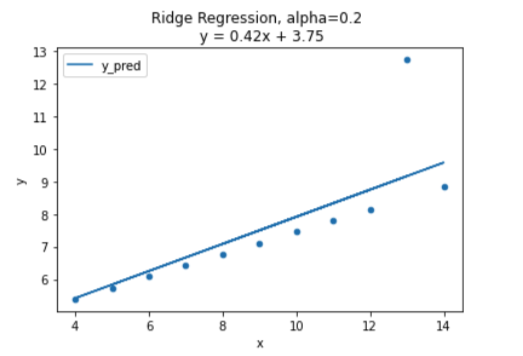
결론
릿지회귀를 이용하여 모델을 만들면 나중에 testdata를 돌릴때 발생할 수 있는 overfitting문제를 해결 할 수 있다.
