[CS] 그래프 이론, 트리, 이진트리와 이진탐색트리

그래프 이론

그래프 이론은 현실 세계에서의 관계를 표현하는 강력한 도구로, 정점과 간선의 조합으로 구성

1. 정점과 간선

• 정점(Vertex, Node): 개별적인 객체나 위치를 나타냄. 사람, 도시, 물체 등이 될 수 있음
• 간선(Edge): 정점을 연결하는 선으로, 정점 간의 관계를 나타냄. 방향이 있는 경우도 있고 없는 경우도 있음
• 가중치(Weight): 간선에 부여된 값으로, 간선을 통과하는 비용이나 거리를 나타냄. 정점 간 이동 비용. 최단 거리를 찾거나 네트워크 문제를 해결 시 중요

2. Indegree, outdegree

• indegree: 특정 정점으로 들어오는 간선의 수
• outdegree: 특정 정점에서 나가는 간선의 수

트리 (Tree Data Structure)

계층적이며 부모와 자식 노드 간의 관계로 이루어진 자료 구조

1. 트리의 특징

• 계층 구조: 부모-자식 관계를 가지며, 각 노드는 부모 노드로부터 파생
• 유일 무이한 경로: 두 노드 간의 경로는 유일하게 존재하며, 특정 노드에서 다른 노드로 가는 경로는 단 하나.

2. 노드의 분류

-루트 노드: 트리의 가장 상단에 있는 노드로, 모든 다른 노드에게 부모.

• 내부 노드: 최소 하나의 자식 노드를 가지는 노드로, 루트 노드와 리프 노드 사이에 위치.
• 리프 노드: 자식 노드가 없는 노드로, 트리의 끝에 위치.

3. 트리의 높이와 레벨

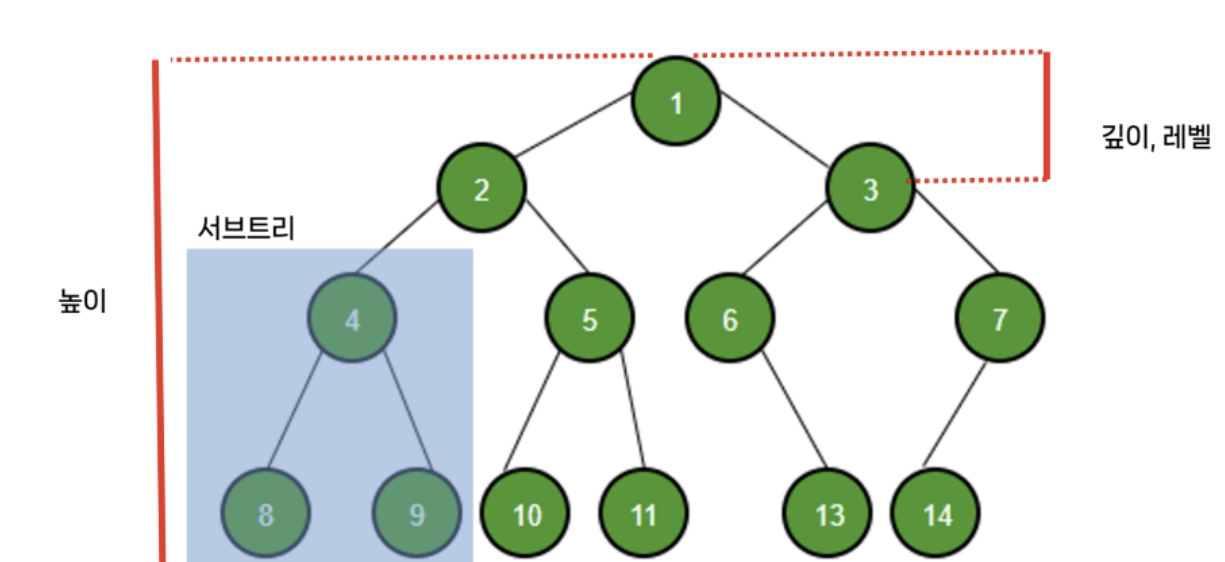
• 깊이 : 트리에서의 깊이는 각각의 노드마다 다르며, 루트 노드에서 특정 노드까지 최단거리로 갔을 때의 거리를 뜻함
  ex) 4번 노드의 깊이 = 2
• 높이: 루트 노드부터 리프 노드까지의 거리 중 가장 긴 거리
  ex) 위 트리의 높이 = 3
• 레벨: 문제마다 조금씩 다르지만 보통 깊이와 같은 의미를 가짐.
  ex) 1번 노드를 0레벨, 2번 노드, 3번 노드를 1레벨로 할 수도 있고, 1번 노드를 1레벨, 2,3번 노드를 2레벨로 할 수도 있다
• 서브트리: 트리 내의 하위 집합. 트리 내에 있는 부분집합
  ex) 4, 8, 9번 노드가 이 트리의 하위집합으로 "서브트리" 에 해당

4. 숲 (forest)

• 트리로 이루어진 집합. 여러 개의 독립적인 트리가 모여 이루는 구조

이진 트리(Binary Tree)와 이진탐색 트리(BST, Binary Search Tree)

1. 이진 트리의 정의

각 노드의 자식 노드 수가 2개 이하로 구성되어 있는 트리

2. 이진 트리의 분류

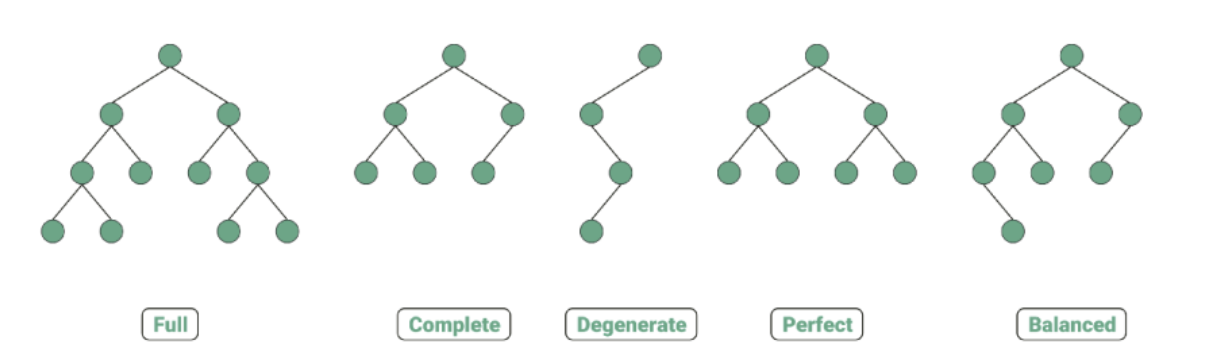
• 정이진트리(full binary tree): 자식 노드가 0개 또는 2개인 이진 트리
• 완전이진트리(complete binary tree): 왼쪽에서부터 채워져있는 이진트리. 마지막 레벨을 제외하고는 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 경우 왼쪽부터 채워져 있음
• 변질이진트리(degenerate binary tree): 자식 노드가 하나밖에 없는 이진 트리
• 포화이진트리(perfect binary tree): 모든 노드가 꽉 차있는 이진 트리
• 균형이진트리(balanced binary tree): 모든 노드의 왼쪽 하위 트리와 오른쪽 하위 트리의 깊이 차이가 1 이하인 트리. map, set을 구성하는 레드블랙트리는 균형이진트리 중 하나

3. 이진탐색트리(BST)

각 노드의 왼쪽 하위 트리에는 노드 값보다 작은 값들이, 오른쪽 하위 트리에는 노드 값보다 큰 값들이 있는 특별한 형태의 이진 트리

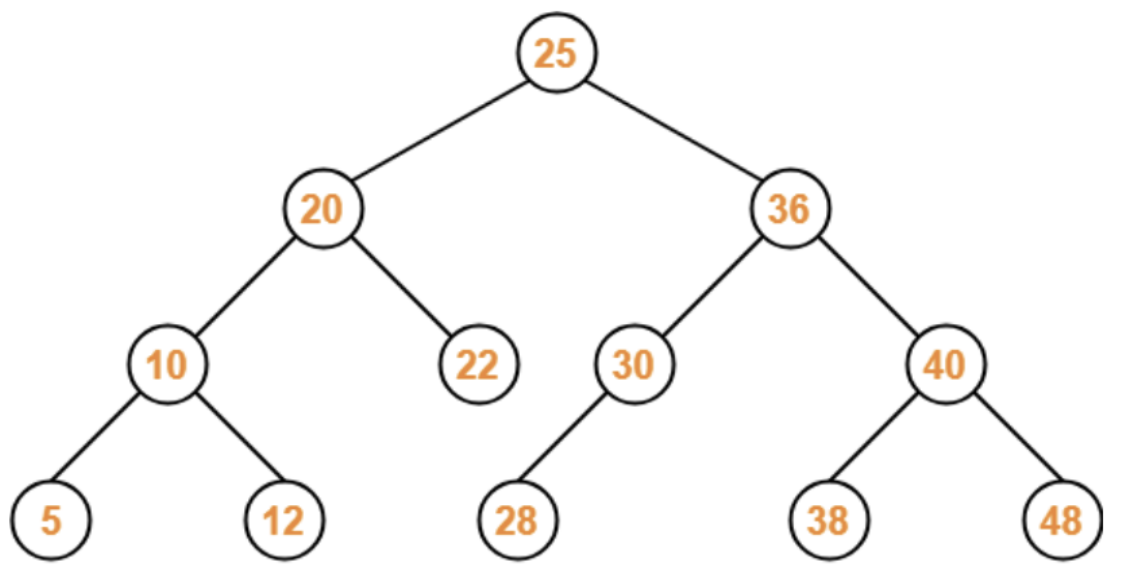
• 탐색 용이성: 노드의 값보다 작은 값을 왼쪽에, 큰 값을 오른쪽에 두기 때문에 효율적인 탐색이 가능.
• 삽입, 삭제, 수정: 균형잡힌 이진탐색트리의 경우 O(logN)의 시간 복잡도
  • 하지만 이진탐색트리는 삽입 순서에 따라 선형에 가까운 자료구조가 될 수 있음 -> 삽입 순서와 상관 없이 트리의 노드들을 회전시키는 방법을 통해 "균형잡히게 만든" 이진 탐색트리로는 AVL 트리, 레드블랙트리가 있음
  • map의 경우 균형잡힌 트리인 레드블랙트리를 기반으로 구현되었기에 삽입, 탐색, 수정, 삭제의 시간복잡도가 모두 O(logN)임을 보장받음

---

REF