[ADsP] 데이터 분석 - 통계분석

💡 통계분석의 이해

◽ 통계

특정집단을 대상으로 수행한 조사나 실험을 통해 나온 결과에 의해 요약된 형태의 표현

---

◽ 표본 조사, 전수 조사

사 대상의 범위에 따라 전수조사와 표본조사로 구분한다.

◾ 전수 조사

대상 집단 모두를 조사하는데 많은 비용&시간이 소요되므로 특별한 경우를 제외하고는 사용되지 않는다.

◾ 표본 조사

• 대상 집단의 일부를 추출 해 어떤 현상을 관측/조사해 자료 수집하는 방법으로 대부분의 설문조사가 표본조사로 진행된다.
  
  
• 모집단의 정의, 표본의 크기, 조사방법, 조사기간, 표본추출방법을 정확히 명시해야 한다.

---

◽ 표본 조사의 주요 용어

◾ 모집단(Population)

조사하고자 하는 대상 집단 전체

◾ 원소(Element)

모집단을 구성하는 개체

◾ 표본(Sample)

조사하기 위해 추출한 모집단의 일부 원소

◾ 모수(Parameter)

표본 관측에 의해 구하고자 하는 모집단에 대한 정보

---

◽ 표본 추출 방법

대상 집단의 일부를 추출해 어떤 현상을 관측/조사해 자료 수집하는 방법

◾ 단순랜덤 추출법 (Simple Random Sampling)

• n개의 번호를
  임의로 선택해 해당 원소를 표본으로 추출
  
  
• 크기가 n인 모든 가능한 표본에 동일한 산출 기회 를 부여한다.(각 샘플은 선택될 확률이 동일하다)
  
  
• 비복원 추출, 복원 추출(추출한 element를 다시 집어넣어 추출하는 경우)
  
  
  

◾ 계통추출법(Systematic Sampling)

• 단순랜덤추출법을 변형한 방식이며, N개 원소로 구성된 모집단에서 k개씩 n개구간(K=N/n) 나누고 첫 구간에서 하나를 임의 선택 후 k개씩 띄어 n개의 표본을 선택해 표본 추출하는 방식.
  
  
• 각 구간별로 동일한 위치의 항목을 추출하는 방법
  
  
  

◾ 집락추출법(Cluster Random Sampling)

• 모집단이 집락(cluster)의 결합으로 구성돼있는 경우 일부 집락을 랜덤 으로 선택 하고 선택된 각 집락에서 단순랜덤 추출법을 수행하는 방법.

• 집락내는 이질적 , 군집간은 동질적

• 모든 자료를 활용하거나 샘플링하는 방법

• 지역표본추출, 다단계표본추출
  
  
  

◾ 층화추출법(Stratified Random Sampling)

• 각 계층 고루 대표 할 수 있게 표본 추출. 이질적 모집단 원소 를 유사한 것 끼리 몇 개의 층(stratum)으로 나눈 후 각 층에서 랜덤하게 표본 추출 하는 방법.

• 비례층화추출법, 불비례층화추출법

---

◽ 측정(measurement)

표본조사나 실험을 실시하는 과정에서 추출된 원소들이나 실험 단위로부터 주어진 목적 에 적합 하도록 관측해 자료를 얻는 것

❓ 실험 : 특정 목적 하에서 실험 대상에게 처리한 후 그 결과 관측해 자료 수집하는 방법

◾ 1) 명목척도(nominal scale)

측정 대상이 어느 집단에 속하는지 분류 할 때 사용 (성별, 출생지 구분)

◾ 2) 순서척도(서열척도 | ordinal scale)

측정 대상의 서열관계 를 관측하는 척도 (만족도, 선호도, 학년, 신용등급)

◾ 3) 구간척도(등각척도 | interval scale)

측정 대상이 갖고 있는 속성의 양을 측정 하는 것으로 구간이나 구간 사이의 간격이 의미가 있는 자료 (온도, 지수)

• 두 관측값 사이 비율은 별 의미없다.
  
  

◾ 4) 비율척도 (ratio scale)

간격(차이)에 대한 비율 이 의미를 가지는 자료, 절대적 기준인 0이 존재 하고, 사칙연산이 가능하며 제일 많은 정보를 가지는 척도 (무게, 나이, 시간, 거리)

• 질적척도

  • 범주형 자료, 숫자들의 크기 차이가 계산되지 않는 척도 (명목척도, 순서척도)

• 양적척도

  • 수치형 자료, 숫자들의 크기 차이를 계산 할 수 있는 척도 (구간척도, 비율척도)
    
    

• 순서척도는 명목척도와 달리 매겨진 숫자의 크기를 의미있게 활용할 수 있다. (예 : 1등이 2등보다 성적이 높다.)

• 구간척도는 절대적 크기는 측정할 수 없기 때문에 사칙연산 중 더하기 와 빼기는 가능 하지만 비율 처럼 곱하거나 나누는 것 은 불가능하다.
  
  
  

---

◽ 통계분석(statistical analysis)

• 특정한 집단이나 불확실한 현상을 대상으로 자료를 수집해 대상 집단에 대한 정보를 구하고 적절한 통계분석방법을 이용해 의사결정을 하는 과정 (통계적 추론)
  
  

◾ 기술통계[Descriptive Statistic]

• 주어진 자료로부터 어떠한 판단이나 예측과 같은 주관 이 섞일 수 있는 과정을 배제하여 통계집단들의 여러 특성을 수량화 하여 객관적인 데이터로 나타내는 통계분석 방법론

• Sample에 대한 특성인 평균, 표준편차, 중위수, 최빈값, 그래프, 왜도, 첨도 등을 구하는 것

◾ 통계적 추론[Inference Statistics|추측통계]

• 수집된 자료를 이용해 대상 집단 "모집단"에 대한 의사결정을 하는 것

• 제한된 표본 을 바탕으로 모집단에 대한 일반적인 결론을 추정하는 것 (본질적으로 불확실성을 수반한다.)

---

💡 추정과 가설검정

◽ 모수 추정

전수조사가 불가능할 때 모집단에서 표본을 추출하고 이를 근거로 확률론을 활용해 모집단의 모수들을 추론하는 것

점추정 [Point Estimation]	모수가 특정한 값일 것이라고 추정하는 것 표본의 평균, 중위수, 최빈값 등을 사용하는 것
구간추정 [Interval Estimation]	점추정의 정확성을 보완하기 위해 모수의 참값 이 포함되어 있다고 추정되는 구간을 결정 하는 것 실제 모집단의 모수 가 신뢰구간에 꼭 포함되어 있는 것은 아니다. 구해진 구간 안에 모수가 있을 가능성의 크기 [신뢰수준, Confidence Interval]가 주어져야 한다.

◾ 구간추정

• 모수가 특정한 구간에 있을 것이라는 개념으로 신뢰구간을 추정하는 방법

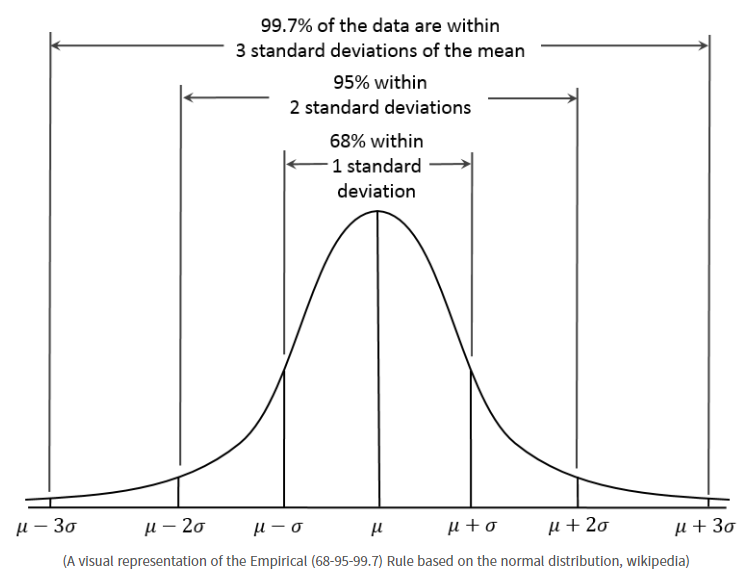
• 신뢰수준: 90%, 95%, 99%의 확률을 이용하는 경우가 많다.

• 신뢰수준 95%: 한 개의 모집단에서 동일한 자료의 개수의 확률표본을 무한히 많이 추출하여 각 확률표본마다 신뢰구간 을 구하면, 이 무한히 많은 신뢰구간 중 95%의 신뢰구간이 미지의 모수를 포함한다는 의미.

• 모집단의 획률분포를 정규분포라 가정할 때, 95% 신뢰수준 하에서 모평균 μ 의 신뢰구간

---

◽ 가설검정

• 모집단에 대한 귀무가설(H0)과 대립가설(H1)을 설정한 뒤, 표본관찰 또는 실험 을 통해 하나를 선택하는 과정

• 귀무가설이 옳다는 전제하에서 관측된 검정통계량의 값보다 더 대립가설을 지지하는 값이 나타날 확률을 구하여 가설의 채택여부 결정한다.

귀무가설 [Null Hypothesis, H0]	현재까지 주장되어온 것이나 변화나 차이가 없음 을 설명하는 가설
대립가설 [Alternative Hypothesis, H1]	귀무가설에 반대되는 주장을 하는 가설로 귀무가설을 기각했을 때 받아들여지는 가설 실제 검정대상 이 되는 가설은 아니다.
검정통계량 [Test Statistic]	관찰된 표본으로부터 구하는 통계량 검정 시 가설의 진위 를 판단하는 기준
유의수준 [Significance Level, α]	귀무가설을 기각 하게 되는 확률의 크기로 "귀무가설이 옳은데도 이를 기각하는 확률의 크기"
유의확률 [p-value]	귀무가설이 맞다고 정할 때, 표본통계량보다 극단적인 결과가 실제로 관측 될 확률 p-value와 α를 비교하여 귀무가설 기각 여부를 결정[p-value<α이면 기각]
기각역 [Critical Region,C]	귀무가설을 기각시키는 검정통계량들의 범위[반대는 채택역(acceptance region)} 귀무가설이 옳다는 전제 하에서 구한 검정통계량의 분포에서 확률이 유의수준 α인 부분

---

◽ 가설검정의 오류

• 제1종 오류와 제2종 오류는 상충관계 가 있다.

• 제1종 오류의 확률을 0.1, 0.05, 0.01 등으로 고정시킨 뒤, 제2종 오류가 최소 가 되도록 기각역을 설정 한다.

• 기각역: 귀무가설을 기각하는 통계량의 영역

• 제 1종 오류[Type 1 error] : 귀무가설 H0가 옳은데도 귀무가설을 기각 하게 되는 오류

• 제 2종 오류[Type 2 error] : 귀무가설 H0가 옳지 않은데도 귀무가설을 채택 하게 되는 오류

	귀무가설(H0)이 사실이라고 판정	귀무가설(H0)이 사실이 아니라고 판정
귀무가설(H0)이 사실	옳은 결정	제 1종 오류(α)
귀무가설(H0)이 사실이 X	제2종 오류(β)	옳은 결정

---

💡 분석 기획 확률 및 확률분포

◽ 확률

특정한 사건이 일어날 가능성의 척도

• 모든 사건 E의 확률값은 0과 1사이에 있다. 0 <= P(E) <= 1
  
  

• 전체 집합 Ω의 확률은 1이다. 즉, P(Ω) = 1
  
  

• 서로 배반인 사건들 E1, E2...의 합집합의 확률은 각 사건들의 확률의 합이다.
  (배반사건 = 교집합이 공집합인 사건)
  
  

• 표본공간(sample space,Ω) :

  나타날 수 있는 모든 결과물의 집합

• 원소(element)

  나타날 수 있는 개개의 결과

• 사건(event)

  표본공간의 부분집합

• 표본공간의 부분집합인 사건의 확률은 P(E)는 표본공간의 원소의 개수에 대한 사건의 개수의 비율로 다음과 같이 정의한다

   P(E) = n(E) / n(Ω)

• 확률 변수(random variable)

  • 특정값이 나타날 가능성이 확률적으로 주어지는 변수
    
    
  • 정의역(domain) 이 표본공간 , 치역(Range)이 실수값인 함수
    
    
  • 0이아닌 확률을 갖는 실수값의 형태에 따라 이산형 확률변수와 연속형 확률변수로 구분된다.

---

◽ 이산형 확률변수

• 0이 아닌 확률 값을 갖는 확률 변수를 셀 수 있는 경우(확률질량함수)

• 이산형 확률변수의 Ex): 동전 2개를 던져서 앞/뒷면이 나오는 경우의 수

• 이산형 확률 변수의 기대값
  

◾ 베르누이 확률분포(Bernoulli distribution)

• 결과가 2개만 나오는 경우 (예시 : 동전 던지기, 시험의 합격/불합격 등).

• 기대값 E(x) = p

• 분산 var(x) = p(1-p)
  

◾ 이항분포(Binomial distribution)

• 베르누이 시행을 n번 반복했을 때 k번 성공할 확률

• 확률변수 x의 밀도함수가 다음과 같을 때, X는 모수가 (n,p)인 이항분포를 갖는다.
  

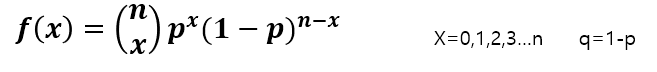
◾ 기하분포(Geometric distribution)

• 성공확률이 p인 베르누이 시행에서 첫 번째 성공이 있기까지 n번 실패할 확률

• 확률변수 x의 pdf가 다음과 같이 주어질 때, x는 모수가 p인 기하분포를 가진다.
  

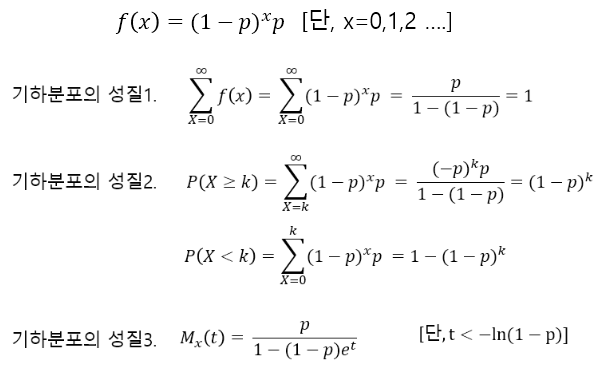
◾ 다항분포(Multinomial distribution)

• 이항분포를 확장한 것으로 세가지 이상의 결과를 가지는 반복 시행에서 발생하는 확률 분포
  
  

◾ 포아송분포(Poisson distribution)

• 시간과 공간 내에서 발생하는 사건의 발생횟수에 대한 확률분포(예 : 책에 오타가 5page 당 10개씩 나온다고 할 때, 한 페이지에 오타가 3개 나올 확률)

• 확률변수 x의 pdf가 다음과 같을 때 x는 모수가 λ인 포아송 분포를 가진다.
  

---

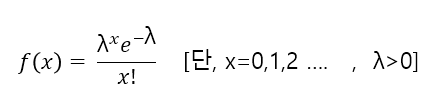
◽ 연속형 확률변수(continuous r.v.)

• 확률 변수들이 기대값으로부터 벗어나는 정도

• 가능한 값이 실수의 어느 특정구간 전체에 해당하는 확률변수(확률밀도함수)

• 균일분포 분포가 특정범위에서 균등하게 나타나는 분포

◾ 균일분포(일양분포, Uniform distribution)

• 모든 확률변수 X가 균일한 확률을 가지는 확률분포 (다트의 확률분포)
  
  

◾ 정규분포(Normal distribution)

• 평균이 μ 이고, 표준편차가 σ 인 x의 확률밀도함수

• 표준편차가 클 경우 퍼져보이는 그래프가 나타난다.

• Z= X- μ (평균)δ (표준편차)
  
  

◾ 지수분포(Exponential distribution)

• 어떤 사건이 발생할 때까지 경과 시간 에 대한 연속확률분포이다.
  
  

◾ t-분포(t-distribution)

• 표준정규분포와 같이 평균이 0을 중심으로 좌우가 동일한 분포를 따른다.

• 표본의 크기가 적을때는 표준정규분포를 위에서 눌러 높은 것과 같은 형태를 보이지만 표본이 커져서(30개 이상) 자유도가 증가하면 표준정규분포와 거의 같은 분포가 된다.

• 데이터가 연속형일 경우 활용한다.

• 두 집단의 평균이 동일한지 알고자 할 때 검정통계량으로 활용된다.

◾ x2-분포(chi-square distribution)

• 모평균과 모분산이 알려지지 않은 모집단의 모분산에 대한 가설 검정에 사용되는 분포이다.

• 두 집단 간의 동질성 검정에 활용된다. (범주형 자료에 대해 얻어진 관측값과 기대값의 차이를 보는 적합성 검정에 활용

◾ F-분포(F-distribution)

• 두 집단간 분산 의 동일성 검정에 사용되는 검정 통계량의 분포이다.

• 확률변수는 항상 양의 값만 갖고 x2분포와 달리 자유도를 2개 가지고 있으며 자유도가 커질수록 정규분포에 가까워진다.

---

💡 모수 검정, 비모수 검정

◽ 모수 검정

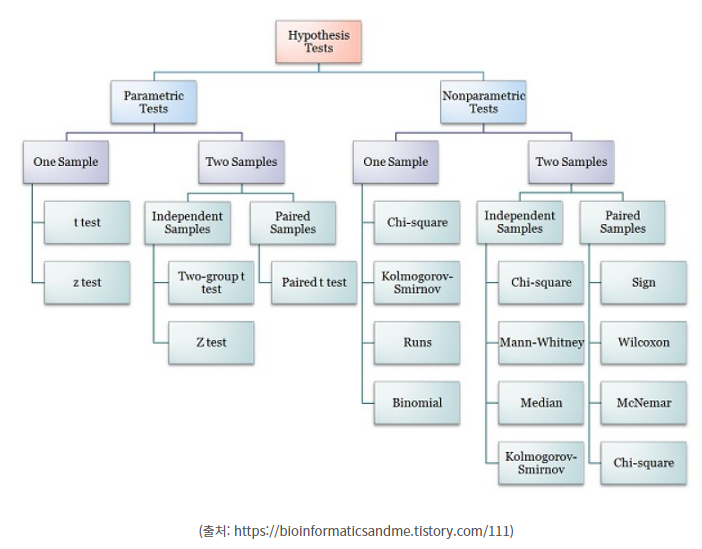
• 모집단의 분포에 대한 가정을 하고, 그 가정 하에서 검정통계량과 검정통계량의 분포를 유도해 검정을 실시하는 방법

• 가설의 설정 : 가정된 분포의 모수(모평균, 모분산 등) 에 대한 가설 설정

• 검정 실시 : 관측된 자료를 이용해 표본평균, 표본분산 등을 구하여 검정 실시

◽ 비모수 검정

• 모집단의 분포에 대해 아무 제약을 가하지 않고 검정을 실시하는 검정 방법

• 관측 자료가 특정분포를 따른다고 가정할 수 없는 경우에 이용

• 가설의 설정 : 가정된 분포가 없으므로, 단지 '분포의 형태'가 동일한지 여부에 대해 가설 설정

• 검정 실시 : 관측값의 순위 나 관측값 차이 의 부호 등을 이용해 검정 실시
  (ex) 부호검정, 순위합검정, 부호순위합검정, U검정, 런검정, 순위상관계수 등

---

본 게시물에 포함된 내용은 한국데이터산업진흥원에서 발행한]
[데이터 분석 전문가 가이드, 2019년 2월 8일 개정,https://logoflife.tistory.com/26]에 근거한 것임을 밝힙니다.