[ADsP] 데이터 분석 - 기초통계분석

박진우·2022년 6월 23일

ADsP ARIMA 기초통계분석 다차원 척도법 데이터 분석 분해시계열 시계열 주성분 분석

ADsP

목록 보기

10/16

💡 기술통계(Descriptive Statistics)

자료를 요약 하는 기초적 통계

데이터 분석에 앞서 데이터의 대략적인 통계적 수치 를 계산해봄으로써 데이터에 대한 대략적 이해 와 분석에 대한 통찰력 을 얻기에 유리하다.
데이터 마이닝에 앞서 데이터의 기술통계를 확인해보는 것이 좋다.
data

내장된 데이터 프레임을 워크스페이스 안에 로드하여 쓸 수 있게 해주는 함수
head

데이터를 기본 6개를 보여주어 데이터가 성공적으로 import 되었는지 살펴볼 수 있는 함수
summary
데이터의 컬럼에 대한 전반적인 기초 통계량 (Min, Max, 1st Qu., 3rd Qu, Median, Mean)
특정 컬럼의 통계량 구하기
mean(iris$Sepal.Length), median(), sd(), var(), quantile(), min(), max()
특정 column 선택 :데이터네임$column명

◽ 인과관계의 이해

◾ 용어

종속변수(반응변수,y) : 다른 변수 의 영향을 받는 변수
독립변수(설명변수,x) : 영향을 주는 변수
산점도(scatter plot) : 좌표평면 위에 점들로 표현한다.
- 두변수 사이의 선형관계, 함수관계, 이상값 존재, 몇 개의 집단으로 구분 되는가 확인한다.

◽ 공분산(covariance)

두 확률변수 X, Y의 방향의 조합 (선형성 )
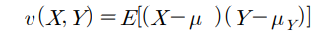
X, Y가 독립 이면 Cov(X,Y)=0

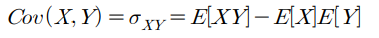
◽ 단순회귀분석과 중회귀분석(다중회귀분석)의 개념

연속 변수로 측정된 두 변수간의 선형 관계 를 분석하는 기법
데이터 안의 두 변수 간의 관련성을 파악하는 방법이다.
두 변수의 상관관계 를 알기위해 상관계수(correlation coefficient)를 이용한다.

상관분석 유형

피어슨의 상관계수 (Pearson correlation)	스피어만 상관계수 (Spearman correlation)
등간척도 이상으로 측정되는 두 변수들 간의 상관관계 측정 두 변수 간의 선형관계의 크기를 측정하는 값으로 비선형적인 관계는 나타내지 못한다. - 연속형 변수만 가능하다. ex) 국어 점수와 영어점수의 상관계수	서열척도인 두 변수들의 상관관계 측정 두 변수 간의 비선형적인 관계도 나타낼 수 있다. - 연속형 외에 이산형 순서형도 가능하다. ex) 국어성적 석차와 영어성적 석차의 상관계수

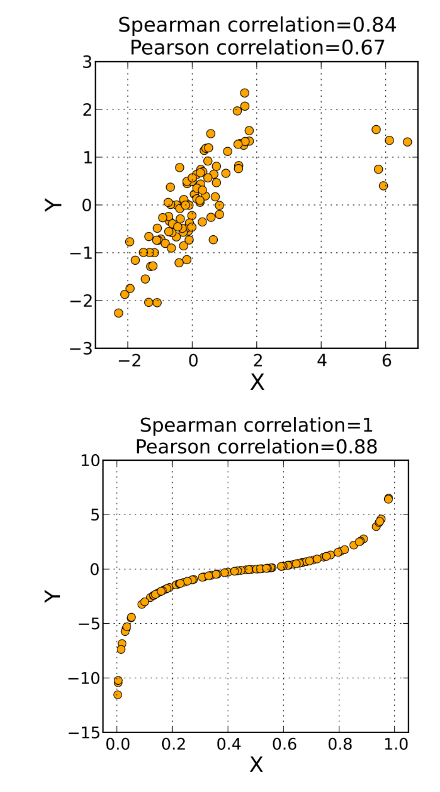
◾ 상관계수와 상관관계

상관계수 r의 범위: -1 ≤ r ≤ 1
상관계수가 0에 가까울 수록 상관이 낮다 고 말한다.
(단, r=0 ➡️ 두 변수간 직선적 관계가 없다는 의미이다.

◾ 결정계수

회귀 분산분석
총 제곱합(총 변동, SST) = 회귀제곱합(설명된 변동, SSR) + 오차제곱합(설명안된 변동, SSE)
R^2(결정계수) = 회귀제곱합(SSR) / 총 제곱합(SST)
➡️ 결정계수가 클 수록 회귀방정식 과 상관계수 의 설명력이 높아진다.

◾ 피어슨 표본 상관계수

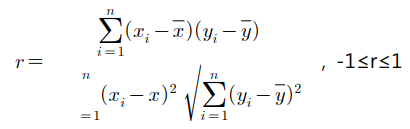
◾ 스피어만 상관계수

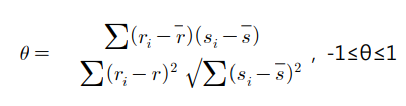
💡 회귀 분석 (Regression Analysis)

◽ 단순회귀분석과 다중회귀분석의 개념

회귀분석 : 하나나 그 이상의 독립변수들이 종속변수 에 미치는 영향 을 추정,추론하는 통계기법
- 종속변수 or 반응변수 : 영향을 받는 변수 ➡️ y
- 독립변수 or 설명변수 : 영향을 주는 변수 ➡️ x, x1, x2 ...

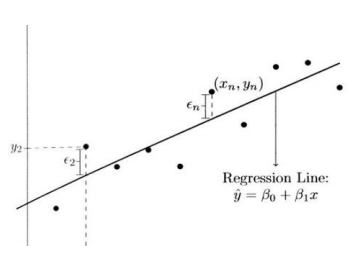
◾ 단순선형회귀

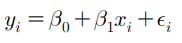
회귀모형 중에서 가장 단순 한 모형
한 개의 독립변수와 하나의 종속변수로 구성
오차항 있는 선형관계
회귀계수의 추정치는 보통 제곱오차를 최소 로 하는 값으로 구한다.

◾ 다중회귀분석(중회귀)

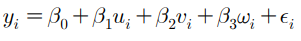
종속변수에 있어서 2개 이상의 독립변수에 대한 회귀식을 추정하는 방식

단순회귀모형이 종속변수의 변동을 설명하는데 ~~충분하지 않다~~는 점을 보완
두 개 이상의 독립변수를 사용하여 종속변수의 변화 를 설명

ex) 덥고 (x1) 습하면 (x2) 아이스커피 판매량(y)이 늘어난다.

◽ 찾은 선이 적절한지 확인

모형이 통계적으로 유의미한가 ➡️ F통계량(p값) 확인

F 통계량 확인, F통계량의 p-값이 0.05 보다 작으면 추정된 회귀식은 통계적으로 유의미하다고 한다.
회귀계수들이 유의미한가 ➡️ 계수의 t값, p값 또는 신뢰구간 확인
모형이 얼마나 설명력을 갖나 ➡️ 결정계수(R-square) 확인

결정계수를 확인, 결정계수는 0에서 1값을 가짐, 높은 값을 가질수록 추정된 회귀식의 설명력이 높다.
모형이 데이터를 잘 적합하고 있나 ➡️ 잔차 그래프 & 회귀진단
회귀모형에 대한 가정
선형성 : 독립변수의 변화 에 따라 종속변수도 변화 하는 선형인 모형

독립변수의 변화에 따라 종속변수도 일정크기로 변화
독립성 : 잔차와 독립변수의 값이 ~~관련되어 있지 않다.~~

등분산성 : 오차항 들의 분포는 동일한 분산을 가진다.
비상관성 : 잔차들끼리 ~~상관이 없어야 한다.~~
정상성 : 잔차항 이 정규분포 를 이뤄야 한다.

◽ 회귀분석의 종류

lm(y ~ x, data=dfrm) : 단순선형회귀분석
lm(y ~ u+v+w) : 다중선형회귀분석
summary(m) : 결정계수, F통계량, 잔차의 표준오차 등 주요 통계량 정보 확인
plot(df1) : 산점도 그리기
plot(lm(y~x, data=df1) : 회귀식의 그래프
- 만약 회귀식의 잔차도가 뚜렷한 곡선 패턴 을 가지면 오차항은 평균 0, 분산 일정하다는 가정은 ~~만족하지 않는다.~~

◽ 최적회귀방정식의 선택: 설명변수의 선택

회귀모형 설정 변수 선택 원칙

y에 영향 미칠 수 있는
모든 설명변수 x들을 y값 예측에 참여시킨다.
설명변수 x가 많아지면 관리하는데 노력이 많이 요구되므로 가능한 범위 내에서 적은 수의 설명변수를 포함시켜야 한다

💡 설명변수 선택하는 방법

◽ 1) 모든 가능한 조합의 회귀분석 (All possible regression)

모든 가능한 독립변수들의 조합 에 대한 회귀모형을 고려한다.
AIC(Akaike information criterion) or BIC(Bayesian information criterion) 기준으로 가장 적합한 회귀모형 선택 ➡️ 가장 작은 AIB값 혹은 BIC값 을 가지는 모형을 최적모형으로 선택 한다.

◽ 2) 단계적 변수선택 (Stepwise Variable Selection)

◾ 전진선택법 (forward selection)

절편만 있는 상수모형에서 시작,
중요 하다고 생각되는 설명변수 부터 차례로 모형에 추가, 가장 제곱합 을 기준으로 가장 설명을 잘하는 변수를 고려, 그 변수가 유의하면 추가한다.

◾ 후진제거법 (backward elimination)

독립변수 후보 모두 포함한 모형에서 출발,
제곱합을 기준 으로 가장 적은 영향을 주는 변수부터 하나씩 제거 , 더이상 유의하지 않은 변수가 없을 때까지 설명변수들을 제거

◾ 단계별방법 (stepwise method)

전진선택법에 의해 변수를 추가 하면서 새롭게 추가된 변수에 기인해 기존 변수가 그 중요도가 약해지면 해당변수 제거 하는 등 단계별로 추가 or 제거되는 변수의 여부 검토, ~~더이상 진행하지 않고~~ 중단 한다.

◾ step(lm(종속변수~설명변수, 데이터세트), scope=list(lower=~1, upper=~설명변수), direction="변수선택방법")

lm : 회귀분석
scope : 분석시 고려할 변수의 범위 / 가장 낮은 단계 lower에 1 입력시 상수항 의미, 가장 높은 단계 설정하기 위해서는 설명변수들 모두 써줘야 한다.
direction : 변수 선택방법, 선택 가능 옵션은 forward(전진선택법), backward(후진선택법), both(단계적방법)

💡 시계열 예측

◽ 정상성

시계열자료 (Time-series Data) : 시간의 흐름에 따라 관측된 데이터
시계열분석 (Time Series Analysis)를 위해서는 정상성 (Stationary) 만족 해야 한다.
정상성 : ~~시점 상관없이~~ 시계열의 특성 이 일정하다는 것
- 1) 평균이 일정하다.
- 2) 분산이 시점 에 ~~의존하지 않는다.~~
- 3) 공분산은 단지 시차에만 의존 , 시점 자체에는 ~~의존하지 않는다.~~
정상성의 조건을 하나라도 ~~만족하지 않음~~ ➡️ 비정상 시계열 (대부분 시계열 자료) ➡️ 정상성 만족하도록 정상 으로 만든 후 분석 수행

◽ 비정상 시계열 자료의 분석을 위한 작업

◾ 정상성 만족 여부 판단

이상점과 개입을 살핀다.
개략적인 추세 유무를 관찰( 상승 또는 하락 추세가 있다면 ~~평균이 일정하지 않는다.~~)

◾ 비정상 시계열을 정상성을 만족하도록 수정

이상점 존재 ➡️ 이상값 제거
개입 ➡️ 회귀분석 수행
추세 ➡️ 차분(현 시점의 자료값에서 전 시점의 자료값을 빼는 것)
분산이 일정하지 않음 ➡️ 변환

💡 시계열 모형

시계열을 분석하기 위한 모델은 4가지가 있다.

▶ 자기 회귀 모델 (AR)

▶ 이동 평균 모델 (MA)

▶ 자기회귀 이동평균 모델(ARMA)

▶ 자기회귀 누적 이동평균 모델(ARIMA)

✔ MA 최적 차수 - 자기 상관 함수(ACF)
✔ AR 최적 차수 - 부분 자기 상관 함수(PACF)

◽ 자기회귀모형(AR모형)

현 시점의 자료가 p시점 전까지 유한개의 과거 자료로 설명될 수 있다. (p차 자기회귀모형)
AR 모형인지 판단하기 위해 자기상관함수(ACF)와 부분자기상관함수(PACF)를 이용한다.
AR(p) 모형은 부분자기상관함수(PACF)가 p+1 시점 이후 절단 한다.

◽ 이동평균모형(MA[Moving Average model] 모형)

과거 와 현재 자신의 오차 와의 관계를 정의한 것이다.
AR 모델의 수식과 차이점은 Z에서 오차항 인 알파 로 바뀐것이다.
현 시점의 자료를 p시점 전까지 유한개 백색잡음들의 선형결합으로 표현
항상 정상성을 만족 하는 모형으로 ~~정상성 가정이 필요없다.~~
MA 모형인지 판단하기 위해 자기상관함수(ACF)와 부분자기상관함수(PACF)를 이용한다.
MA(q) 모형은 자기상관함수(ACF)가 p+1 시점 이후 절단 한다.

◽ ARIMA (자기회귀 누적이동평균모형)

ARIMA(p,d,q)으로 표현하며, 순서대로 AR 모형 차수, 차분, MA 모형 차수를 의미한다.
최적 차수 ➡️ 자기 상관 함수 (ACF), 편 자기 상관함수 (PACF)를 사용하여 찾아야 한다.
기본적으로 비정상 시계열 모형
차분, 변환을 통해 AR모형이나 MA모형, ARMA 모형으로 정상화

◽ 분해 시계열

시계열에 영향을 주는 일반적인 요인을 분리해 분석하는 방법
회귀분석적인 방법을 주로 사용이다.
이론적 약점이 있음에도 경제 분석, 예측에 널리 사용된다.
각 구성요인을 정확하게 분리하는 것이 중요하지만 ~~쉽지 않다.~~

분해식의 일반적 정의
(시계열 값) = 미지의 함수 (경향(추세)요인, 계절요인, 순환요인, 불규칙요인)

◽ 시계열 구성 요소

◾ 1) 추세요인 (Trend factor)

오르거나 내리는, 이차식, 지수적 형태 등 어떤 특정한 형태를 취하는 경우

◾ 2) 계절요인 (Seasonal factor)

각 월, 각 분기 등 고정된 주기 에 따라 자료가 변화하는 경우

◾ 3) 순환요인 (Cyclical factor)

~~알려지지 않은~~ 주기를 가지고 자료가 변화하는 경우

◾ 4) 불규칙요인 (Irregular factor)

위 세 가지 요인으로 ~~설명할 수 없는~~ 회귀분석에서 오차 에 해당하는 요인

💡 시계열 실습

◾ 1) 시계열 자료 불러오기

'ts' 클래스 : 시계열 자료 형식
일반 데이터셋 ➡️ 시계열 자료 형식으로 변환 : ts함수 사용

◾ 2) 그림 고찰

plot(Nile) : 그래프 추세 확인, 비계절성/계절성 파악

◾ 3) 분해시계열

decompose(Ideaths) : 계절성 을 띄는 시계열 자료를 4가지 요인으로 분해
plot(Ideaths.decompose) : 추세요인, 계절요인, 불규칙요인 으로 분해된 시계열 자료에 대한 그림
Ideaths.decompose$seasonal : 계절성 띄는 시계열 자료에 계절요인을 추정해 그 값을 원 시계열자료에서 빼서 조정 ( 계절요인 제거 )

◾ 4) ARIMA 모형

(1) 차분
- Nile.diff1 <- diff(Nile, differences=1) : 1번 차분
- Nile.diff2 <- diff(Nile, differences=2) : 2번 차분

(2) ARIMA 모델 적합 및 결정
- acf(Nile.diff2, lag.max=20) : 자기상관함수 그래프, lag 개수 20개
- pacf(Nile.diff2, lag.max=20) : 부분상관함수 그래프, lag 개수 20개)
- auto.arima(Nile) : forecast 패키지의 auto.arima 함수 이용하여 적절한 ARIMA 모형 결정
(3) ARIMA 모형을 통한 예측
- Nile.arima <- arima(Nile, order=c(1,1,1)) : 시계열 자료를 ARIMA(1,1,1) 모형에 적합
- Nile.forecasts <- forecast(Nile, arima, h=10) : forecast 패키지의 forecast 함수 이용하여 미래 수치 값 예측, 10개 년도만 예측

◽ 다차원척도법(Multidimensional Scaling, MDS)

개체들의 유사성을 2차원,3차원 으로 표현하는 방법

여러 대상 간의 관계에 대한 수치적 지료를 이용해 유사성에 대한 측정치를 상대적 거리 로 시각화 하는 방법
군집분석과 같이 개체들을 대상으로 변수들을 측정한 후에 개체들 사이의 유사성/ 비유사성을 측정하여 개체들을 2차원 공간상 에 점 으로 표현하는 분석방법

즉 비슷한 개체들끼리 모아서 2차원 그래프로 표현해주는것
입력데이터 는 케이스 간의 유사도(similarity)를 측정한 거리 데이터이며, 출력 결과 는 케이스들이 기하학적 공간상에 배치된 그래프
- 기하학적 공간상에 배치된 케이스 간의 거리는 유사도의 크기를 나타낸다.
  
  즉 유사한 케이스 들은 서로 가까이 위치 하도록 배치, 상이한 케이스 들은 멀리 떨어져 있도록 배치해야 한다.

종류
- 계량적 MDS(Metric MDS): 데이터가 구간척도 or 비율척도인 경우 활용한다.
- 비계랑적 MDS(nonmetric MDS) : 데이터가 순서척도인 경우 활용한다.

◽ 다차원 척도법의 목적

데이터 속에 잠재되어 있는 패턴 또는 구조 를 찾아낸다.
그 구조를 소수 차원의 공간에 기하학적 으로 표현한다.
데이터 축소(Data Reduction)의 목적으로 다차원척도법을 이용한다.

즉, 데이터에 포함되는 정보를 끄집어내기 위해 다차원척도법을 탐색수단으로써 사용한다.
다차원척도법에 의해서 얻은 결과를, 데이터가 만들어진 현상이나 과정에 고유의 구조로서 의미를 부여한다.

cmdscale(eurodist) : 각 도시의 상대적 위치 를 도식화할 수 있는 X, Y좌표 계산
특정 변수들의 ~~관측치가 없더라도~~ 개체 간의 유사성에 대한 자료 사용하여 산점도 그릴 수 있다.

◽ 주성분분석(Principal Component Analysis, PCA)

상관관계가 있는 고차원 자료 를 자료의 변동을 최대한 보존하는 저차원 자료 *로 변환**시키는 방법

자료의 차원을 축약 시키는데 주로 사용
p차원 변수가 주어져 있을 때, X의 선형변환 중 분산이 가장 큰 선형변환을 첫 번째 주성분, X의 선형변환 중 첫 번째 주성분과 상관계수가 0이면서 분산이 가장 큰 선형변환을 두 번째 주성분......p번째 주성분까지 정의 가능
주성분들은 서로 ~~상관관계가 없음~~
주성분들의 분산의 합은 Xi들의 분산의 합과 같다.
ai = i번째 주성분의 로딩

fit = princomp(USArrests, cor=TRUE) : 주성분분석 시행, ~~공분산행렬이 아닌~~ 상관계수 행렬 사용
summary(fit) : 주성분들의 표분편차, 분산의 비율 등을 보여준다.
loadings(fit) : 주성분들의 로딩 벡터 를 보여준다.
plot(fit) : 각 주성분의 분산의 크기를 그림으로 그려준다. ➡️ Scree plot
- 주성분의 분산 감소 가 급격하게 줄어들어 주성분의 개수를 늘릴 때 얻게 되는 정보의 양이 상대적으로 미미한 지점 에서 주성분 개수 정하기
- 주성분들이 설명하는 분산의 비율이 70~90% 사이가 되는 주성분 개수 선택
biplot(fit) : 관측치들을 첫 번째와 두 번째 주성분의 좌표 에 그린 그림

본 게시물에 포함된 내용은 한국데이터산업진흥원에서 발행한]
[데이터 분석 전문가 가이드 2019년 2월 8일 개정, https://logoflife.tistory.com/33?category=803379, https://ko.wikipedia.org/wiki ]에 근거한 것임을 밝힙니다.

박진우

이전 포스트

[ADsP] 데이터 분석 - 통계분석

다음 포스트