추론
resoning inference argument
: 논리를 풀어가는 과정
- 논리를 풀어갈 때 참이라고 인정되는 명제들을 나열하여 자신이 주장하는 결론을 유도한다.
논리는 명제 논리와 술어 논리로 구분된다.
명제 논리
Propositional Logic
: 논리를 일반적으로 주어와 술어를 구분하지 않고 전체를 하나의 식으로 처리하여 참 또는 거짓을 판별하는 법칙
명제
Proposition
: 참 또는 거짓을 명확하게 구분할 수 있는 문장이나 수식
- 객관적인 판단으로 진릿값(참 또는 거짓)으로 표현할 수 있어야한다.
- n개의 단순 명제가 있을 때 진릿값의 경우의 수 :
2^n- 이진 논리 : T(참), F(거짓) 2가지의 진릿값 가진다.
이때 명제들을 연결하여 하나의 명제로 만들어주는 논리 연산자가 있다.
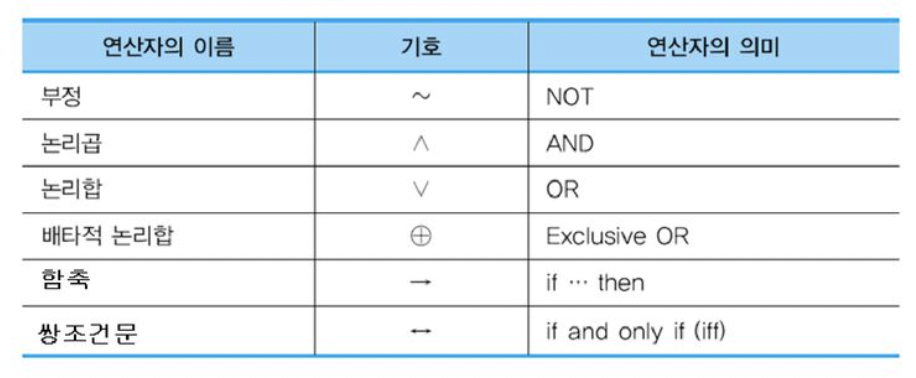
논리 연결자
Logical Connectives
Logical Operators
: 단순 명제들을 연결시켜 주는 역할을 하는
∨, ∧, ¬과 같은 논리 연산자를 논리 연결자 라고한다.단순 명제 : 하나의 문장이나 식으로 된 명제 합성 명제 : 여러 개의 단순 명제들을 논리 연산자들로 연결하여 만들어진 명제
- 논리 기호를 여러 번 사용해 합성 명제를 구성할 경우 합성 명제
P(p,q,r, ...)의 부분 명제p,q,r을변수라고 함.- 합성 명제의 진리값은 각 변수의 진릿값에 의해 구할 수 있음.
- → 논리 연산자 우선순위
부정부터 1번.쌍조건문 = 동치
부정
negative
:
~p¬p= not p , p가 아니다.
논리곱
conjunction
:
p ∧ q= p and q , p 그리고 q
논리합
disjunction
:
p ∨ q= p or q , p 또는 q
배타적 논리합
exclusive_OR XOR
:
p ⊕ q
p와 q의 진릿값 중 하나만 참일 때만 모두 참, 그렇지 않는 경우엔 거짓.
- 명제의 개수 세 개 이상 => 참 명제가 홀수일때만 참이다.
- 논리 회로의 구성에 많이 이용되며 컴퓨터 하드웨어나 통신에서의 자료전송시 패리티 비트 등 다양하게 활용됨.
함축 / 조건 연산자
implication
:
p → q= p 이면 q이다.
- p의 진릿값이 참이고 q의 진릿값이 거짓일때만 : 거짓
함축의 또 다른 표현들1) p이면 q이다. if p then q 2) p는 q의 충분조건이다. p is sufficient for q 3) q는 p의 필요조건이다. q is sufficient for p 4) p는 q를 함축한다. p implies q
동치 / 쌍방조건문
propositional equivalence
biconditional
:
p ↔ q= p이면 q이고 q이면 p이다.
- 명제 p와 q가 모두 참이거나 거짓일때 : 참
쌍방조건문의 또 다른 표현들1) p이면 q이고 q이면 P이다. p if and only if q 2) p는 q의 필요충분조건이다. p is necessary and sufficient for q
역, 이, 대우
converse
inverse
contraposition
p → q일 때q → p를p → q의 역이라고 한다.
¬p → ¬q를p → q의 이라고 함.
¬q → ¬p를p → q의 대우라고 함.
- 대우 : 이에 대한 역을 취한 것.
1) 명제의 역과 이는 서로 대우 관계 2) 명제와 그 명제의 대우는 논리적 동치 관계 3) 이외에는 논리적 동치관계가 존재하지 않음
합성 명제의 진릿값
: 진리표를 사용해 단계적으로 연산함으로써 원하는 합성 명제의 진리값을 보다 쉽고 편리하게 구한다.
- 진리표에 단순 명제들이 가질 수 있는 모든 경우의 진릿값을 표시한 후 합성 명제들을 연산의 순서대로 연산.
항진 명제 ↔ 모순 명제
tautology ↔ contradiction
: 합성명제를 구성하는 단순 명제의 진릿값에 상관없이
합성명제의 연산결과가 항상 참 ↔ 항상 거짓
사건 명제contingency= 항진 명제도 모순 명제도 아닌 명제
예시)p가 단순 명제 일때 p ∨ ¬p 명제 p가 거짓이면 ¬p가 참이 되어 결과가 항상 참인 항진명제 p가 단순 명제 일때 p ∧ ¬p 명제 p가 거짓이면 ¬p가 참이 되어 결과가 항상 거짓인 모순명제
- 항진 명제 부정 : 모순 명제
모순 명제 부정 : 항진 명제
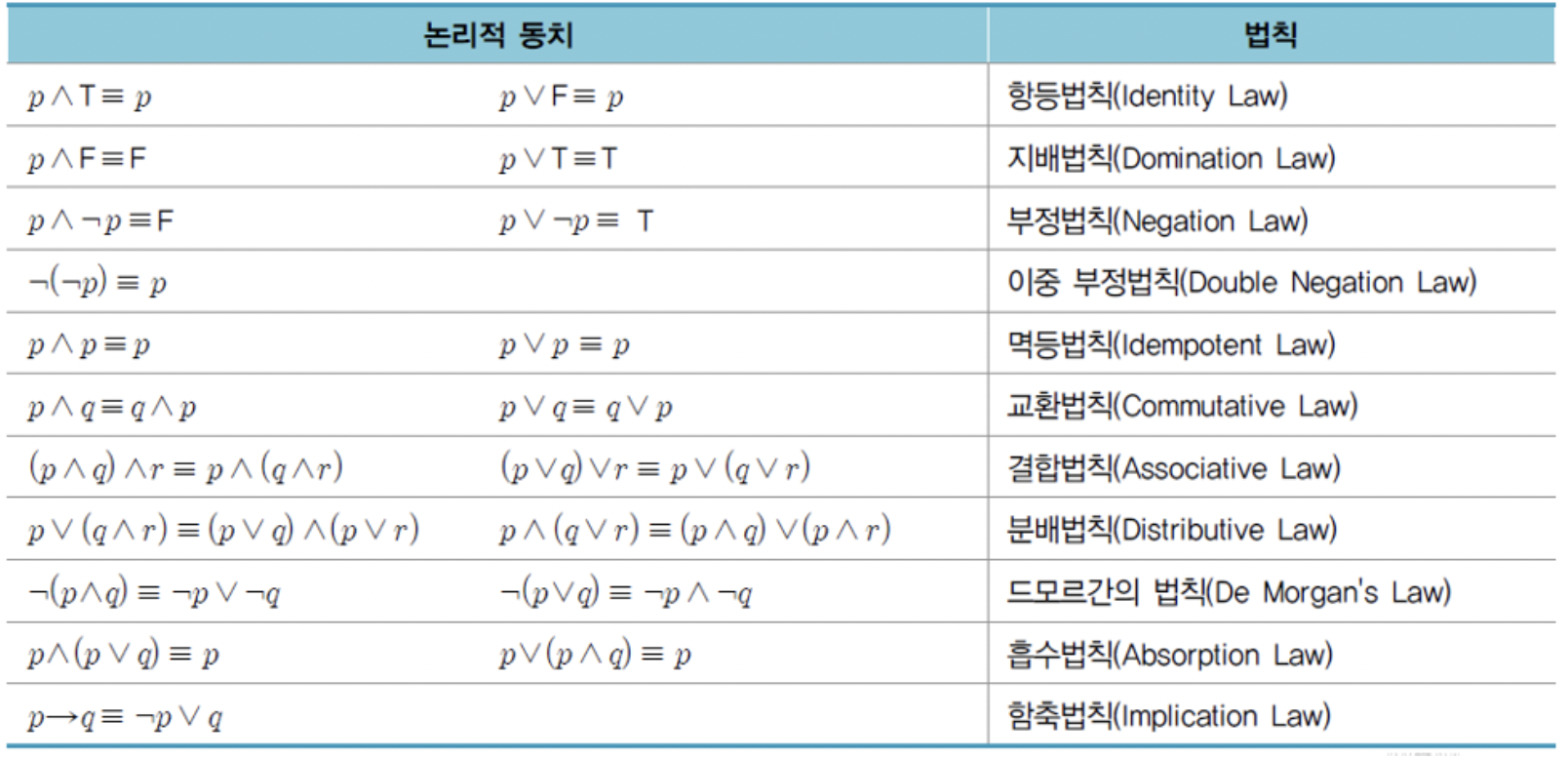
논리적 동치
logical equivalence
: 두 개의 명제 p,q의 쌍방 조건
p ↔ q가 항진 명제이면, 두 명제는 논리적 동치이다.
p ≡ q로 표기
- !! 즉, 두 명제가 논리적 동치라는 것은 명제 p와 q가 같은 논리 값을 가진다는 의미
명제는 참과 거짓이 명확하게 결정되는 것이다.
그럼 변수를 포함하는 명제가 있을때는 참과 거짓을 어떻게 판별할까?
변수의 값에 따라 명제의 참과 거짓이 결정된다.
Ex) x - 7 = 10 에 만족하는 x = 3 밖에 없으며 나머지는 다 거짓이다.
이런경우 x - 7 = 10에 만족시키는 변수 x의 값이 있다. 고 표현한다.
이와 같은 형태의 명제는 P(x)로 표시한다.
P(x) = 변수 x에 대한 명제 술어(propositional predicate)명제 술어에 대한 논리를 술어 논리 혹은 함수 논리 라고 한다.
술어 논리
predicate logic
: 주어와 술어로 구분하여 참 또는 거짓에 관한 법칙
- 대상의 성질을 서술하는 문장들로 이루어짐
대상(변수) : 알파벳 소문자로 나타냄 술어 : 알파벳 대문자로 나타냄문장 x는 P이다 : P(x)
- 하나의 명제를 술어와 객체(상수, 변수 모두 가능)로 분리하여 표현
→ 하나의 술어는 하나 이상의 객체를 수식할 수 있다.- 주어가 될 수 있는 대상에 대한 한정자를 사용할 수 있음.
한정자
quantifier
: 정의역내에서 변수 x만을 지정하는 기호.
즉, 변수를 포함한 명제의 참, 거짓의 판별을 위해 변수의 논의영역을 정하기 위해 사용하는 것.
- 한정기호
전체 한정자(universal quantifier) ∀ : 모든(all)의 의미 Ex) 문장 D에 속하는 모든 x에 대해 P(x)는 참이다 : ∀xP(x) 로 표기 모든 원소가 참이여지 명제가 참이다. 논의영역에 있는 원소 중 하나라도 명제가 거짓이면 거짓이 된다.존재 한정자(Existential quantifier) ∃ : 어떤(some)의 의미 Ex) 문장 P(x)가 참인 x가 존재한다 : ∃xP(x) 논의영역에 있는 원소 중 하나라도 참이면 그 명제함수는 참이다.
명제함수
propositional function
: 변수 x를 포함한 문장 P(x)와 논의 영역(=정의역) D가 있을 떄,
변수 x의 값이 D에 포함되면 문장 P(x)는 변수 x에 대한 명제함수이다.
논의영역
universe of discourse
: 문장이 명제로 명확하게 구분되기 위해 문장 속의 변수 x가 속하는 범위
한정자의 부정
¬(∀xP(x)) => ∃x(¬P(x)) ¬(∃xp(x)) => ∀x(¬P(x))
추론방법
추론
Argument
: 주어진 명제가 참인 것을 전제, 새로운 명제가 참이 되도록 유도해내는 방법
유효 추론
vaild argument
: 주어진 명제가 참이고 유도된 명제가 참인 추론
허위 추론
fallacious argument
: 주어진 명제가 참이고 유도된 명제가 거짓인 추론
전제
premise
: 주어진 명제들
결론
conclusion
: 주어진 명제들에 의해 새로 유도된 명제
주어진 추론에 대한 유효추론 여부 : 진리표를 이용해 전제가 참인 경우 결론이 참인지 거짓인지 확인한다.
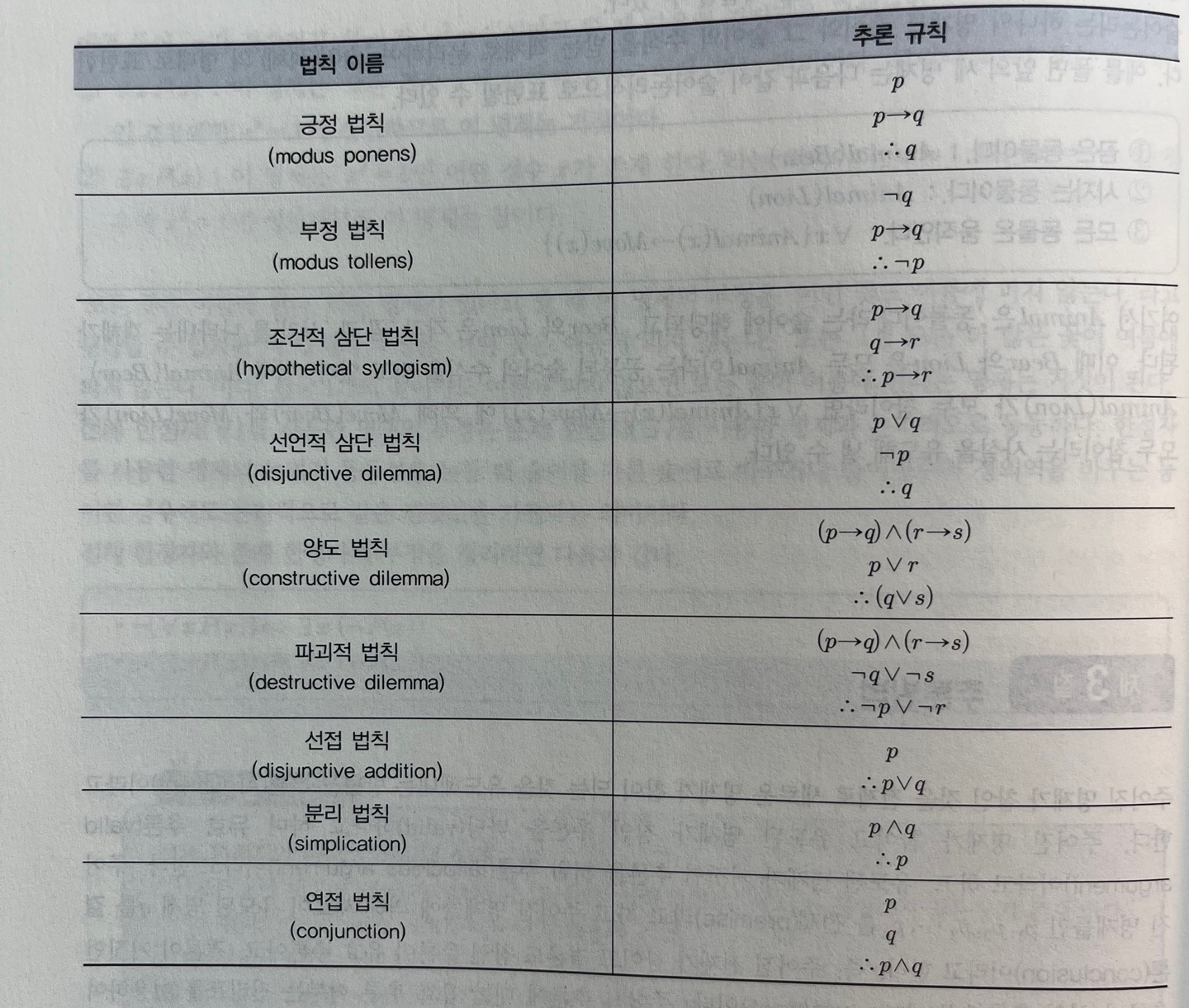
추론 법칙
: 전제 (p1, p2, ...., pn)이 참이면 결론 q가 논리적으로 참이다.
p1, p2, ...., pn ⊢ q여러개의 전제가 있을 경우 추론 법칙을 이용해 타당성을 확인한다.
- 추론에 대한 참 거짓은 명제들과 그들의 진릿값을 비교하여 알 수 있다.
- 결과에 따라 유효 추론인지 허위 추론인지를 알 수 있다.
추론 규칙
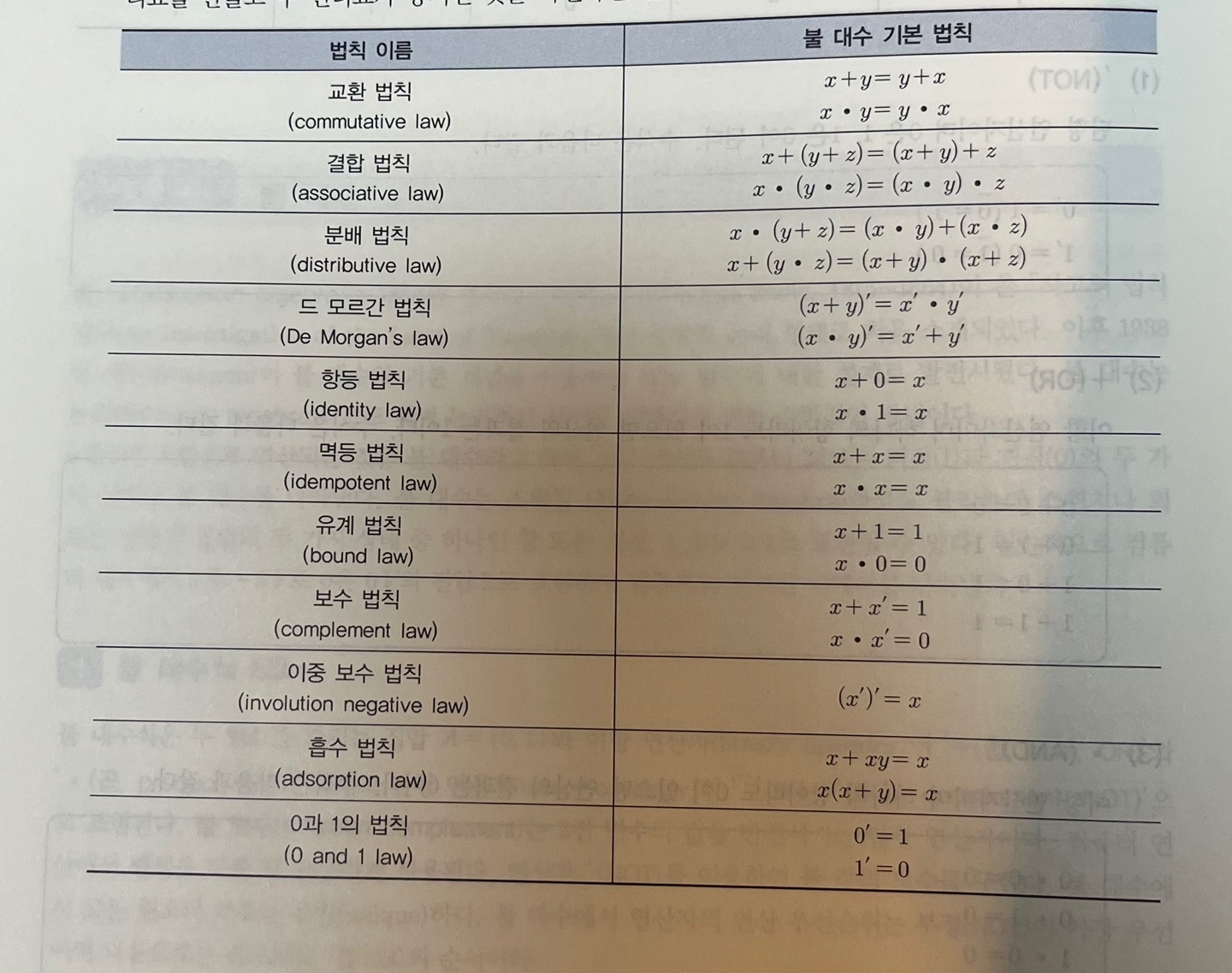
부울 대수 / 논리 대수
boolean algebra logic algebra
: 0과 1의 조합으로 연산되는 것
- 논리적인 문제를 해결하기 위한 수학적인 방법
- 스위칭 대수(switching algebra)이라고도 함.
부울 대수식
두 원소를 가지는 집합
A = {0,1}
1) 이항 연산자+: 합,sum,OR0 + 0 = 0 0 + 1 = 1 1 + 1 = 12) 이항 연산자
•: 곱, product, AND0 • 0 = 0 0 • 1 = 0 1 • 1 = 13) 단항 연산자
'(부정, complement, NOT)0' = 1 / 1' = 0❗️불 대수 연산자 우선순위 :
' > • > +
부울 수식의 표현
0,1 값 외에도 x,y,z와 같은 부울 변수 이용이 가능하다.
Ex) x' + y + z • (x + y') 이와 같은 부울 수식에서 부울 변수가 가질 수 있는 값인 0,1을 정해놓으면 부울 수식에 대한 값을 구할 수 있다.두 부울 수식이 같은 진리표를 가질 경우
동치(equivalence)라고 한다.
함수 f1과 f2가 동치인 경우f1 = f2로 표현한다.
부울 수식 법칙
부울 대수식 표현
부울 함수(boolean function) 로 표현.
: 부울 변수들에 대한 함수
- 부울 함수는 부울 변수와 부울 연산자로 구성된 부울 수식으로 표현
- n개의 부울 변수가 있을 때 그 변수들로부터 얻을 수 있는 조합 갯수 : 2^n
Ex) n개의 부울 변수 x1,x2,...,xn 에 대한 부울 함수 f(x1,x2,...,xn) f(x,y,z) = x + yz
최소항
minterm
: n개의 부울 변수로 만들어지는 진리표에서 변수의 각 항
- n개의 변수 → 2^n개의 최소항을 가짐
- n개의 부울 변수들의 곱으로 표현
변수 x = 1 : x 변수 x = 0 : x'
- 부울 함수는 부울 변수에 대한 최소항 중 1의 값을 가지는 최소항들의 합을 식으로 표현하는 함수
Ex) 세 변수 x,y,z가 각각 x=0, y=1, z=1 일 때 부울 함수 f(x,y,z)의 값이 1이고 나머지의 경우엔 0이라고 할 때 - 011 이므로 최소항은 x'yz 가 된다. - 2^3개의 최소항이 만들어진다.
곱의 합 / 논리합 표준형
sum of products disjunctive normal form, DNF
: 부울 함수를 최소항의 합으로 표현한 것.
최소항 = 부울 변수의 곱 부울 함수 = 최소항들의 합
최대항
maxterm
: n개의 부울 변수들의 합으로 표현
- n개의 변수 → 2^n개의 최대항을 가짐
변수 x = 0 : x 변수 x = 1 : x'
합의 곱
: 부울 함수를 최대항의 곱으로 표현한 것.
최대항 = 부울 편수의 합 부울 함수 = 최대항들의 곱
부울 대수 간소화
부울 대수에 의한 부울식을 체계적으로 간략화시키는 방법들
결국,최소 축약식을 도출하기 위함
- 부울 대수 변수 : 논리회로를 구성하는 게이트의 입력값
- 변수로 이루어진 부울 대수 하나의 항 : 하나의 게이트로 표현
- 복잡한 논리회로의 간소화 = 논리회로를 구성하는 게이트 수와 게이트의 입력을 나타내는 변수의 수를 줄이는 것
논리회로 자체를 직접 간소화하는 것은 어려움
논리식으로 표현 → 부울 대수의 기본 법칙 이용
부울 대수의 기본 법칙 이용
: 부울 수식의 기본 법칙을 이용하여 간소화 하는 것
이 방법은 복잡하고 간소화에 대한 검증이 쉽지 않다.
변수가 많고 항의 수가 많은 경우 더 어려움.
카르노맵
Karnough map
: 부울 변수들에 대한 최소항들을 도표로 그려서 인접한 항들을 서로 묶은 후에 최소화.
- n차 부울 함수에 대해 2^n개의 부울 변수의 조합이 가능
: 2^n 개의 셀을 갖는 카르노맵 작성- 카르노맵을 그리는 법
1) 부울 변수들로부터의 모든 경우의 최소항들을 사각형으로 연결 사각형 연결 : 인접한 사각형끼리는 한 수의 변화만 있게 만들어야함. 2) 최소항들 중 1의 값을 가지는 사각형 안에 '1'을 표시 3) 1로 표시된 사각형들에서 부울 수식의 공통점을 찾아내어 부울 함수를 간소화
- 일반적으로 부울 변수 개수가 2개부터 6개일 때 카르노맵 사용
간소화할 때 같은 부울변수가 각각 0,1의 값을 가진다면 소멸된다.
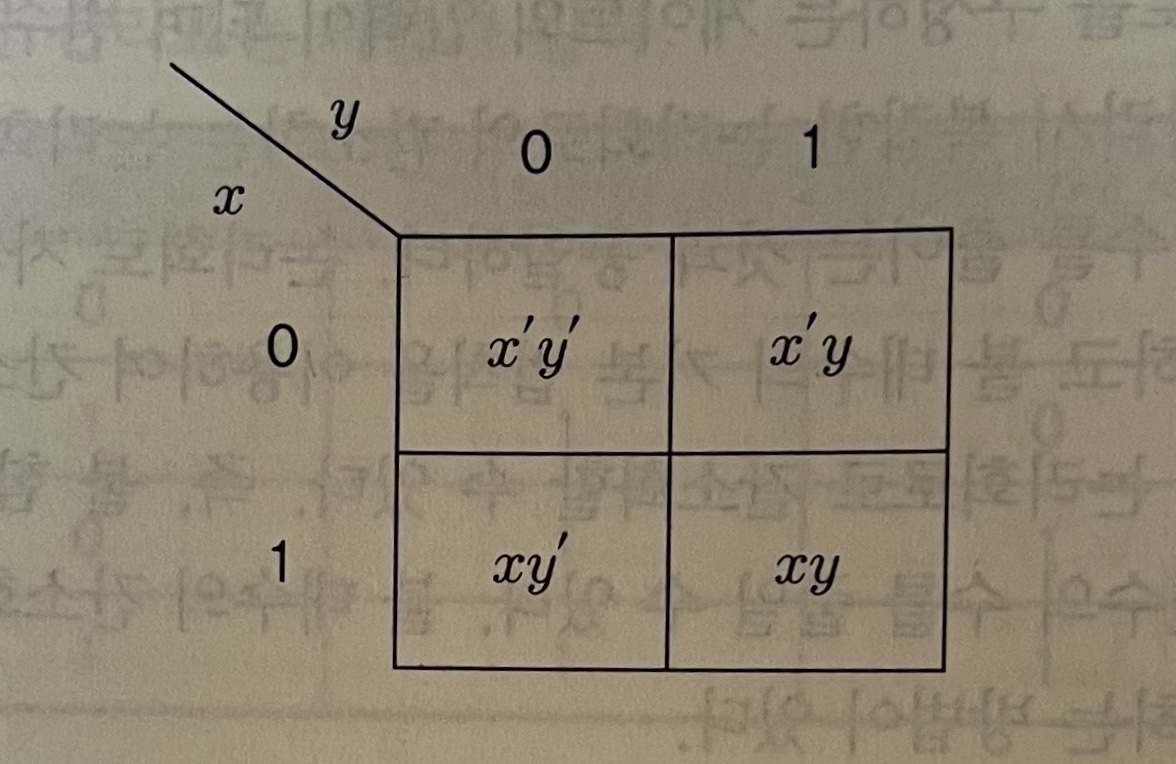
1) 2변수 카르노맵
2) 3변수 카르노맵
- 11(3)과 10(2)의 순서 주의 : 01과 10은 인접할 수 없기 때문
- 오른쪽 끝의 사각형과 왼쪽 끝 사각형은 인접한다.
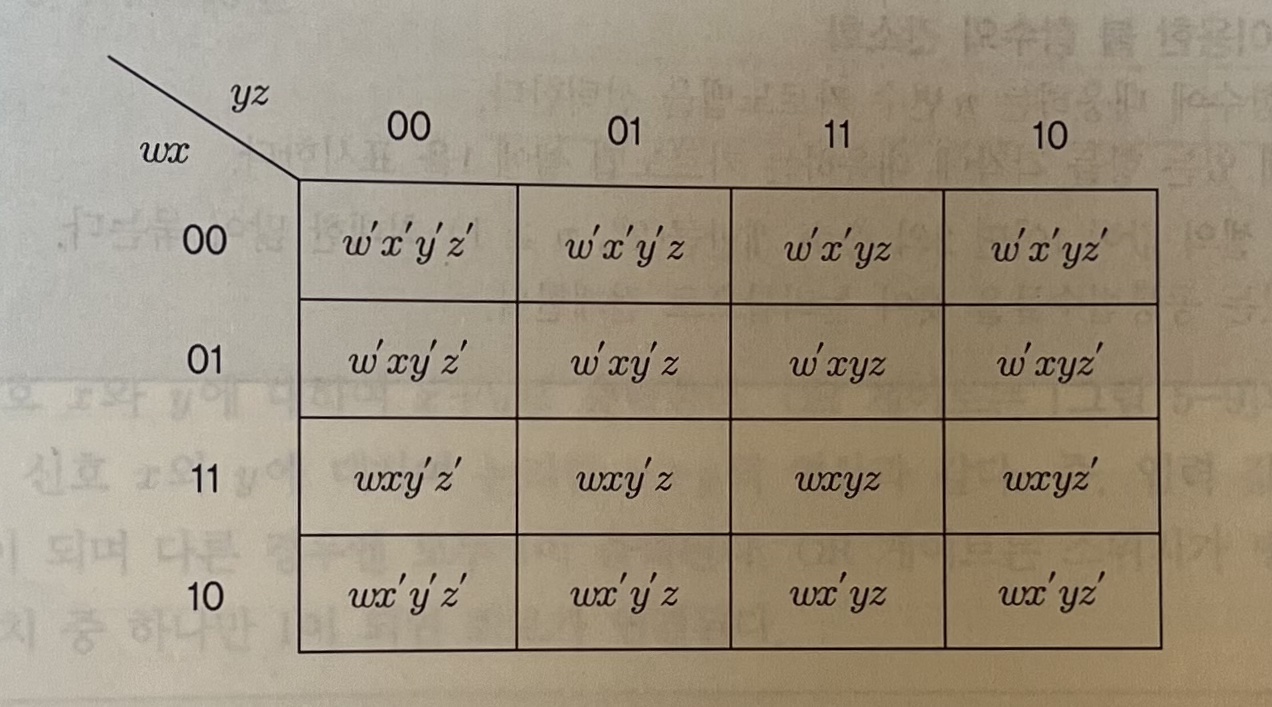
3) 4변수 카르노맵
- 위와 아래의 모서리 사각형들도 인접.
카르노맵을 이용한 부울 함수의 간소화
1) n차 부울 함수에 대응하는 n변수 카르노맵을 선택
2) 부울 함수에 있는 항들 각가에 대응하는 카르노맵 셀에 1 표시
3) 인접하는 셀의 값이 1이면 2의 승수 개만큼 최대한 많이 묶음
4) 묶음에 있는 공통변수드을 찾아 논리합으로 전개부울 대수와 조합회로
부울 대수의 이용 → 복잡한 논리회로 설계를 간단하게 나타낸다.
-> 디지털 신호를 나타내기 위해 사용되는 논리회로는 게이트로 구성됨.
논리 게이트
logic gate
: 논리회로를 구성하는 기본 소자
- 이진 입력 정보를 이용해 0 또는 1의 논리적인 값 생성
논리회로
논리회로는 회로 구조의 특성에 따라 분류된다.
- TV를 비롯한 가전제품에 대부분은 논리회로를 이용함.
1) 순차회로(sequential logic circuit) - 이전 상태의 신호와 외부 입력 신호에 따라 출력이 결정되는 회로 - 이전상태가 계속 유지되려면 출력을 입력에 반영하는 `되먹임 논리회로 구조` - 조합회로에 기억 기능이 추가된 회로2) 조합회로(combinational logic circuit) - 입력 신호만으로 출력이 결정되는 회로 - 일정 시점의 출력값이 일정 시점의 입력값에 의해서만 결정되는 논리회로 - 값을 저장하는 능력이 없음 - 부울 함수로 표현된 식은 컴퓨터에서 사용되는 기본적인 논리 회로를 설계하는데 활용
컴퓨터 회로 설계
입력과 출력 : 논리 회로의 게이트들을 상호연결하여 구성
- 입력 : 부울 변수 - 출력 : 부울 함수 - 부울 연산자 : 게이트 - 논리 값 = 1 : 회로의 스위치 연결된 상태 : ON - 논리 값 = 0 : 회로의 스위치 연결되지 않은 상태 : OFF
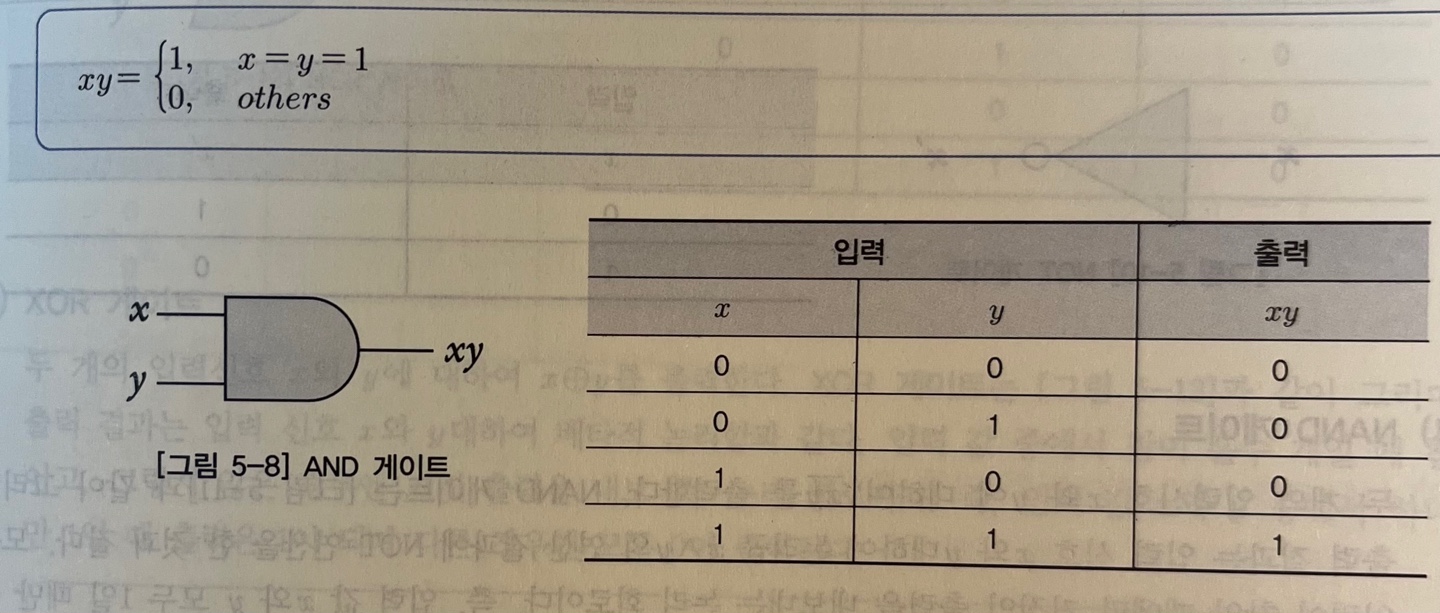
AND 게이트
: 두 개의 입력신호 x와 y에 대해 xy 출력
- 출력 결과 :
x ∧ y: 논리곱 연산와 동일- 스위치 직렬 연결 → 두 스위치 모두 1(ON)여야 회로 연결됨.
OR 게이트
: 두 개의 입력신호 x와 y에 대해 x + y 출력
- 출력 결과 :
x + y: 논리합 연산와 동일- 스위치 병렬 연결 → 두 스위치 중 하나만 1(ON)이면 회로 연결됨.
NOT 게이트
: 한 개의 입력신호 x에 대해 x'출력
- 출력 결과 : 부정
¬x와 동일- 입출력이 서로 반대 : 인버터(inverter)
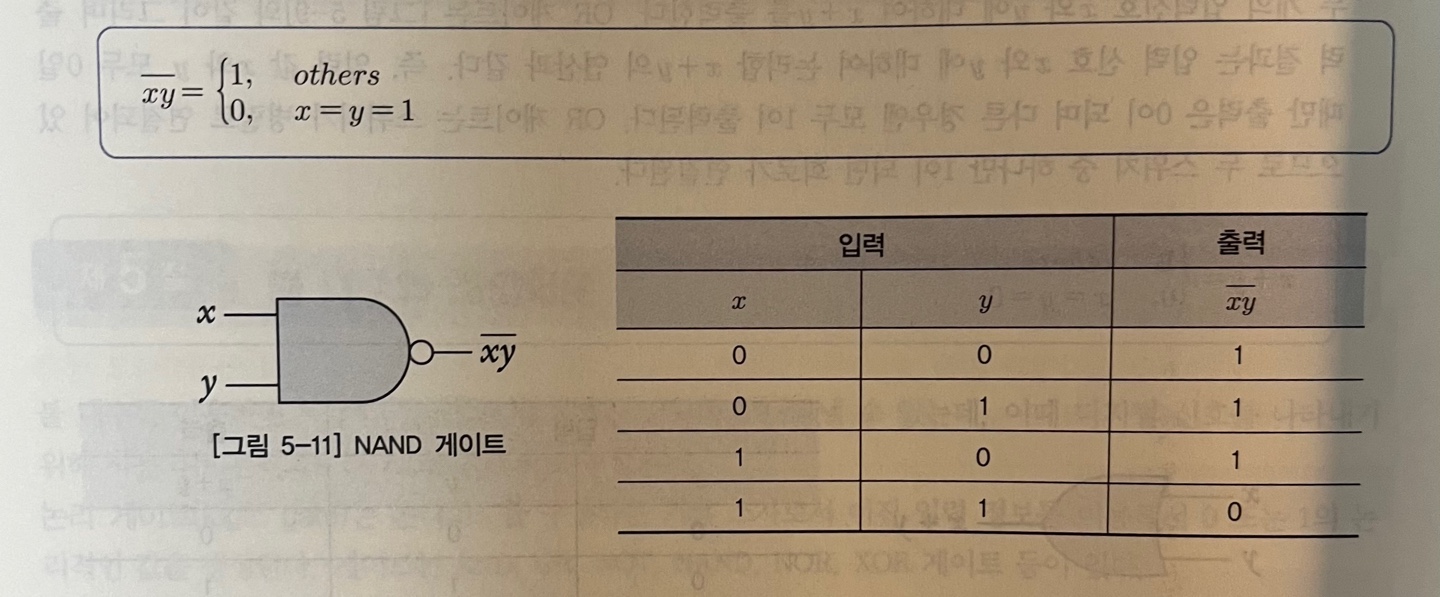
NAND 게이트
: 두 개의 입력신호 x와 y에 대해 (xy)ˉ 출력
- 출력 결과 : AND 게이트 출력부분에 NOT이 붙어있는 것과 동일
- AND 게이트에서 모든 출력 반전
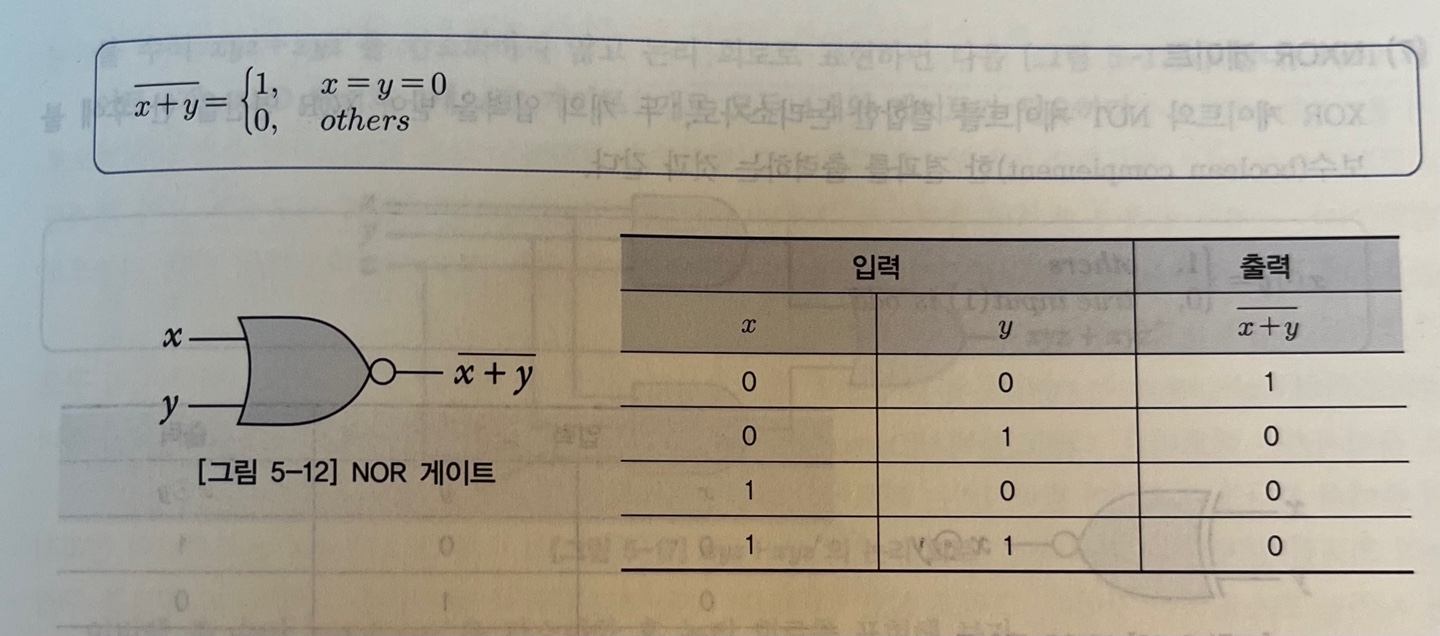
NOR 게이트
: 두 개의 입력신호 x와 y에 대해 (x + y)ˉ 출력
- 출력 결과 : OR 게이트 출력부분에 NOT이 붙어있는 것과 동일
- OR 게이트에서 모든 출력 반전
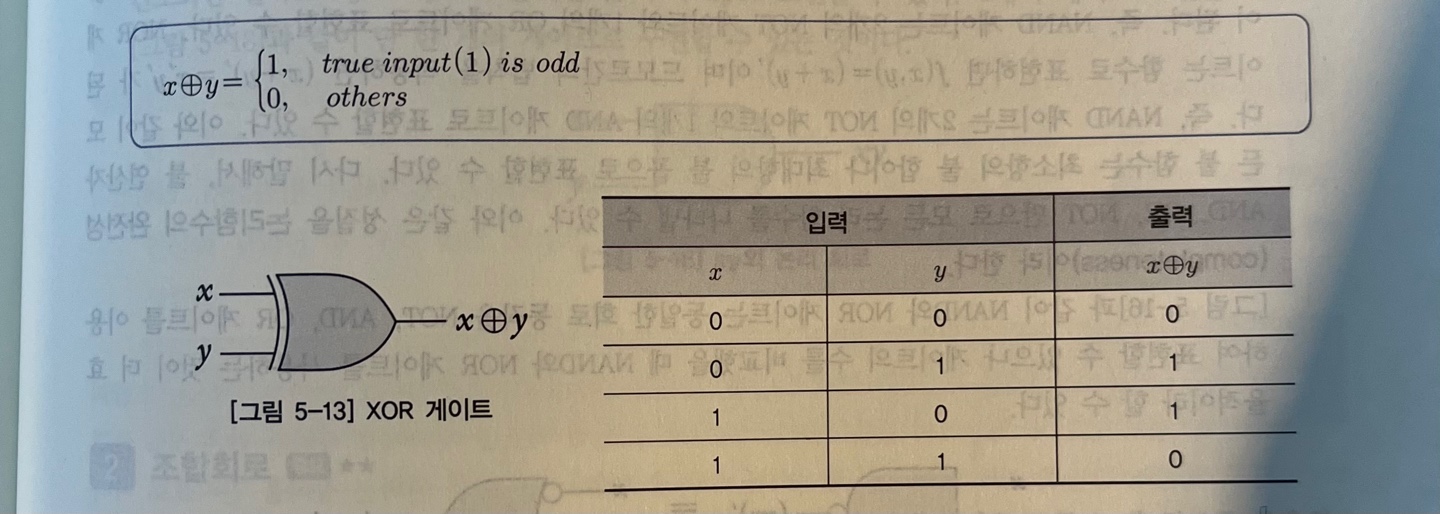
XOR 게이트
: 두 개의 입력신호 x와 y에 대해 x ⊕ y 출력
- 출력 결과 : 배타적 논리합과 동일
- 입력 값 중 참이 홀수 개 : 참 출력
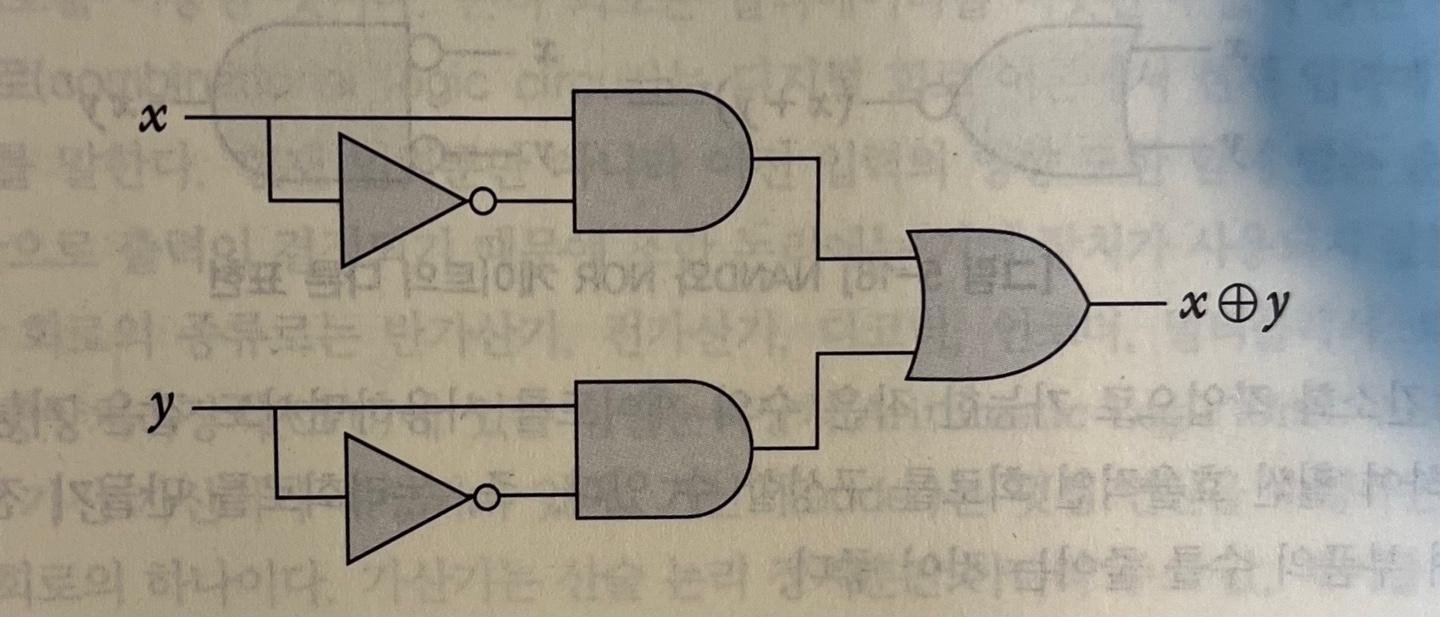
- x ⊕ y 은 x'y + xy' 와 동치
↑ NOT, AND, OR 게이트로 표현 : x ⊕ y = x'y + xy'
NXOR 게이트
: XOR 게이트에 NOT 게이트 결합한 논리소자
- 출력 결과 : XOR 연산 후 부울 보수(NOT)한 결과를 출력한 것과 동일
- x ⊙ y 로 작성
x ⊙ y = xy + x'y'
NAND와 NOR 게이트의 다른 표현
NOT, AND, OR 게이트를 이용해 표현 가능하다.
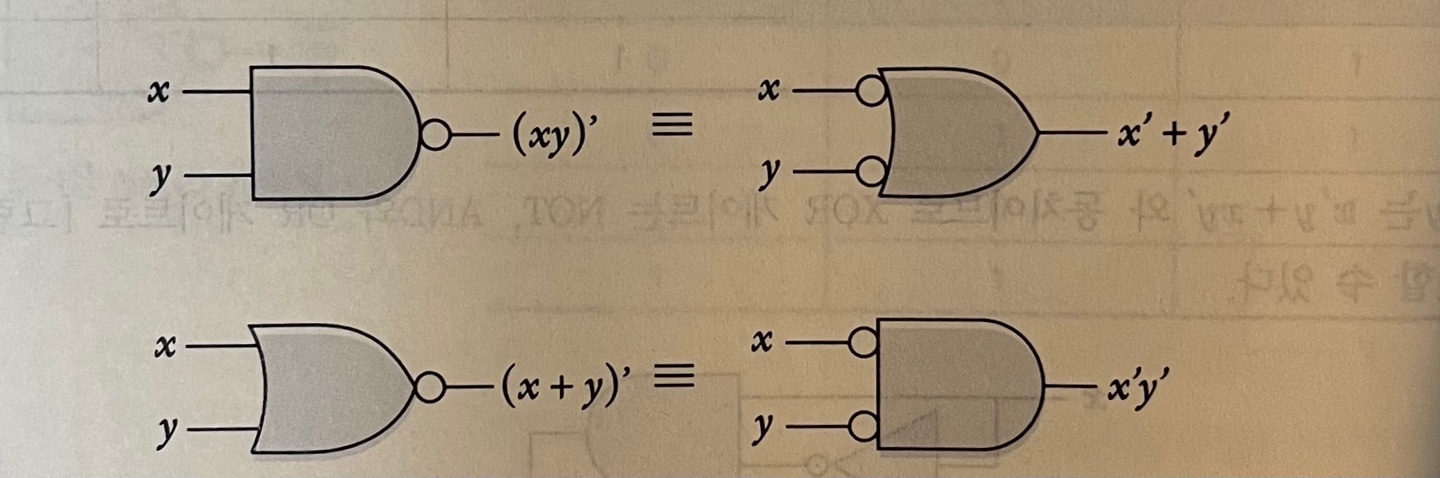
1) NAND 게이트의 함수 표현 : f(x,y) = (xy)' 드모르간 법칙 적용 : (xy)' = x' + y' → 2개의 NOT 게이트 + 1개의 OR 게이트로 표현2) NOR 게이트의 함수 표현 : f(x,y) = (x + y)' 드모르간 법칙 적용 : (x + y)' = x' • y' → 2개의 NOT 게이트 + 1개의 AND 게이트로 표현하지만 게이트의 수가 많아짐으로 NAND, NOR 게이트를 사용하는게 더 효율적이다.
=> 모든 부울 함수는 최소항의 부울 합이나 최대항의 부울 곱으로 표현할 수 있다.
조합회로
Combinational logic circuit
: 현재 입력에 따라 출력을 갖는 논리회로
- 현재 입력뿐만 아니라 이전 입력의 영향 또한 함께 받는 순차 논리와 구별
- 기억장치가 사용되지 않는다.
- Ex) 반가산기, 전가산기, 디코더, 인코더, 멀티플렉서, 디멀티플렉서 등
회로의 예) 중앙처리장치(CPU)에 있는 산술논리장치(ALU) - 조합회로의 하나 - 가산기 내장 : 숫자들을 더하는 기능 - 가산기(Adder) : 덧셈 연산을 수행하는 논리 회로 - 병렬 가산기 : 여러 자리 2진수를 더하기 위한 연산회로 n자리의 bit 덧셈을 위해 n개의 전가산기 필요 : 각각 자리수의 가산기가 필요하기 때문에 가장 하위 자리는 전단에서 올라오는 자리 올림(carry)이 없음으로 반가산기 이용 가능
논리 회로 설계 시 고려할 사항
- 게이트의 입력 및 게이트의 수를 최소화
=> 논리회로의 전파지연 시간을 최소화- 상호 연결되는 수 최소화
조합 논리회로를 구성하는 논리 회로의 설계 과정
1) 주어진 문제 분석 2) 입력 변수, 출력 변수 그리고 출력의 변수명을 결정 3) 진리표를 작성한 후 진리표로부터 부울 함수 구함 4) 진리표에 의한 카르노맵 또는 그 외의 방법으로 간소화 5) 간소화되니 부울 함수에 의해 논리 회로 설계
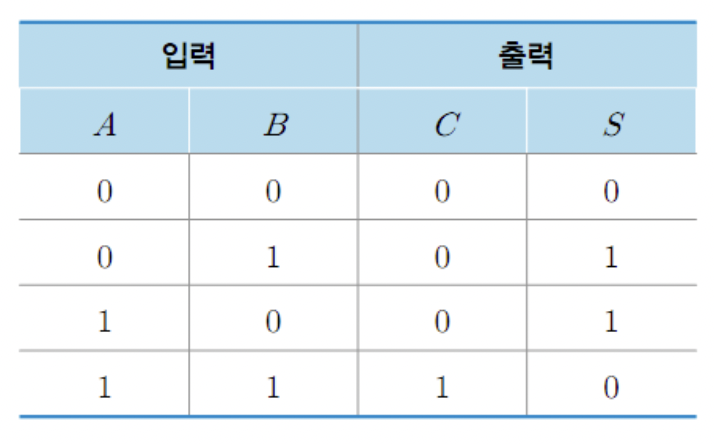
반가산기
Half Adder
: 두 개의 입력 A,B를 받아서 합(Sum)과 자리올림(Carry)을 구하는 조합회로
- 입력 값 : 0 또는 1의 값을 가지는 bit
- 두 입력 비트를 더해 1자리의 합은
S로 출력 : 자릿수
덧셈의 결과로 자리 올림수 발생C로 출력 : 올림수- 입력 값이 모두 1일 때만 자리 올림수 발생
- 반가산기는 전가산기와 다르게 캐리를 고려하지 않는다.
- 두 bit를 더하는 동작의 진리표
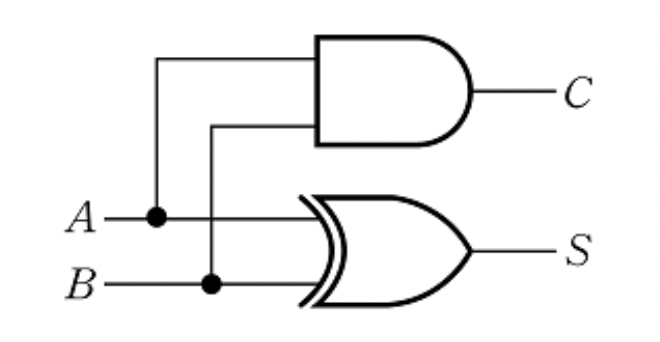
↓ 1에 대한 최소항들의 합을 구해 함수식을 구함S = A'B + AB' = A ⊕ B ↑ 간소화 C = AB
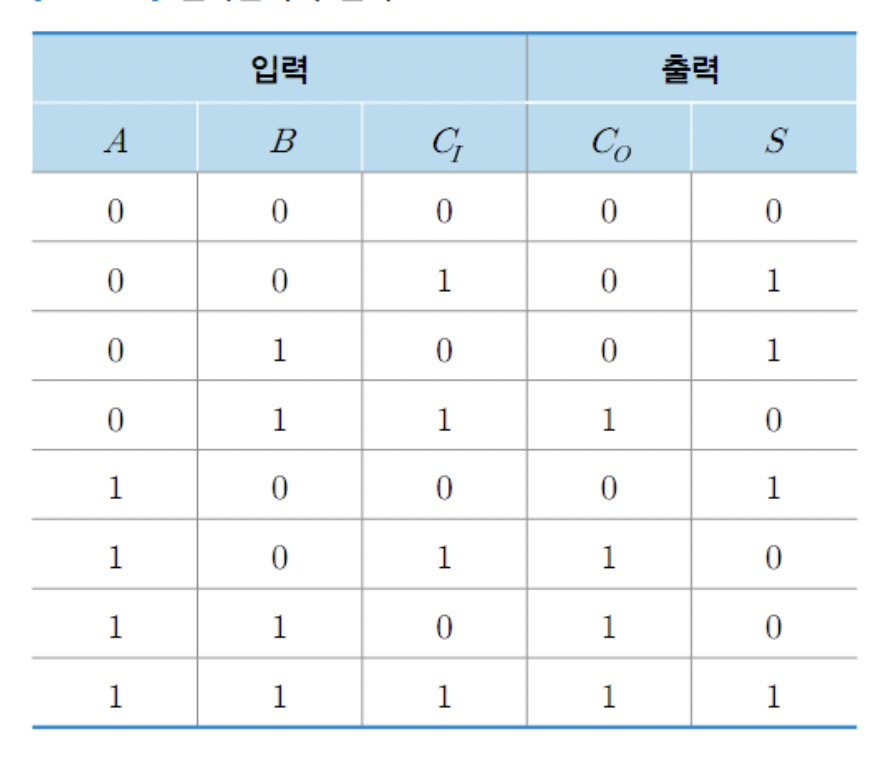
전가산기
Full Adder
: 반가산기 확장(캐리를 고려해 만든 가산기)
- 입력 값 : 두 개의 x,y와 밑의 자리로부터 올라오는 자리 올림수 Ci를 포함한 3개
- 두 개의 출력 S(덧셈 결과), co(덧셈 후 자리올림)에 대해 진리표 작성
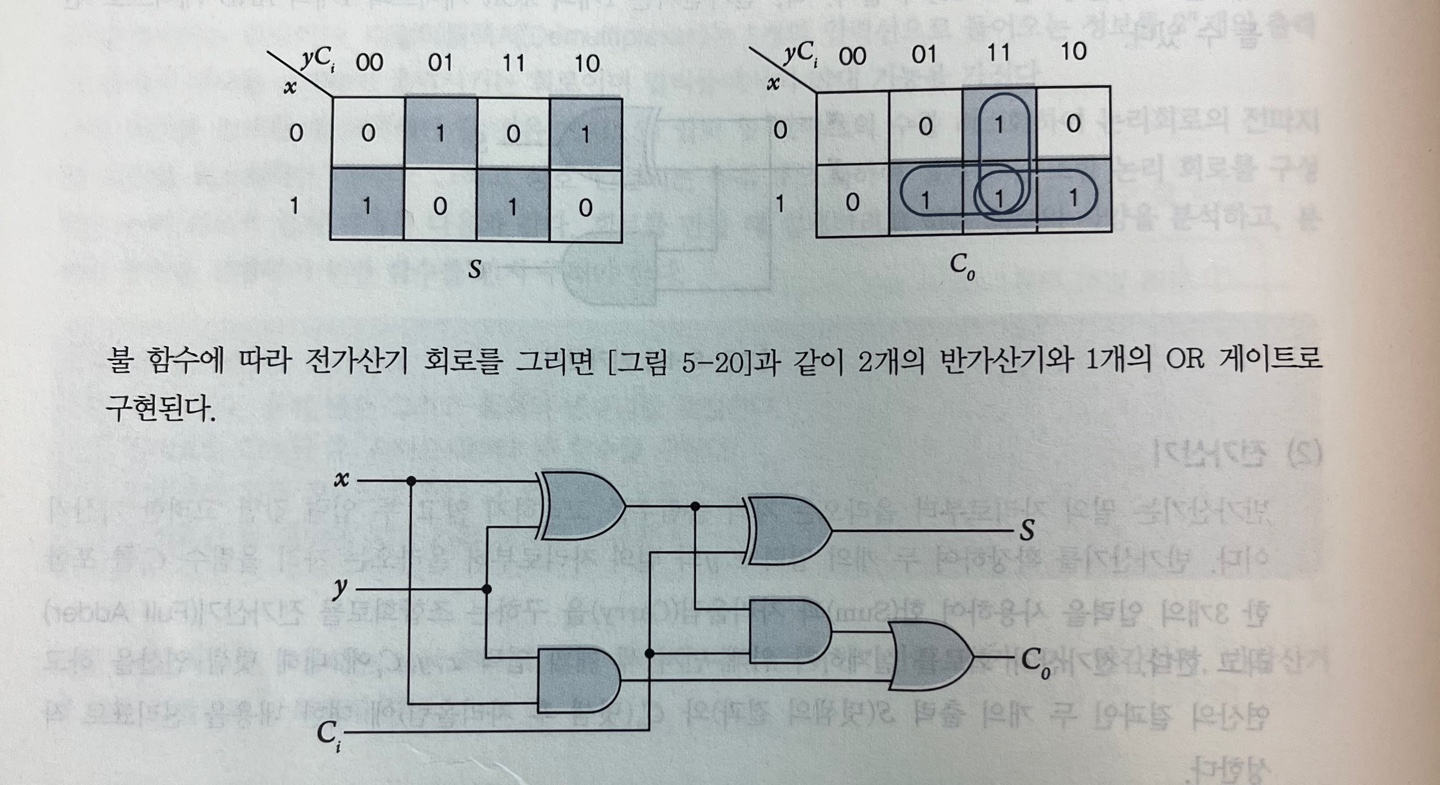
S = A'B'Ci + A'BCi' + AB'Ci' + ABCi = A ⊕ B ⊕ Ci C = A'BCi + AB'Ci + ABCi' + ABCi = ACi + BCi + AB = (A ⊕ B)Ci + AB
- 반가산기 2개 + OR 게이트 = 전가산기
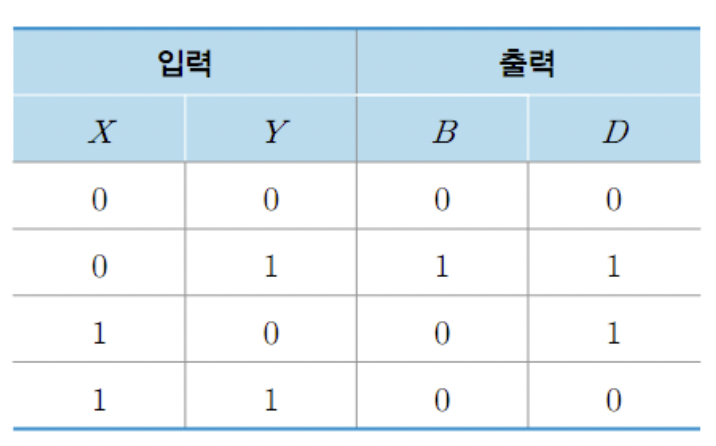
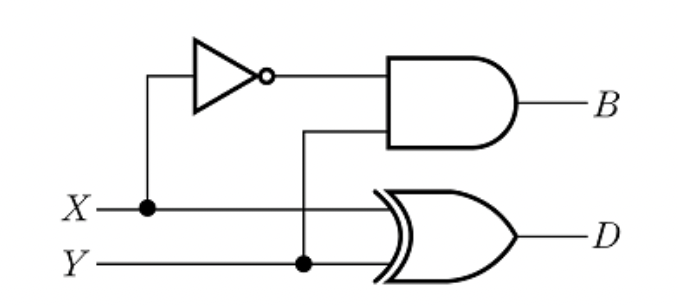
반감산기
Half subtracter
: 두 개의 입력 x,y 대하여 두 값의 차와 피연산수가 연산수보다 작을 경우(모자른 경우) 위의 자리에서 빌려오는 수(Borrow)를 구하는 조합회로
= 빌려오는 수 + 차의 결과 수(출력)
- 두 개의 입력 + 두 개의 출력
D = x'y + xy' = x ⊕ y B = x'y
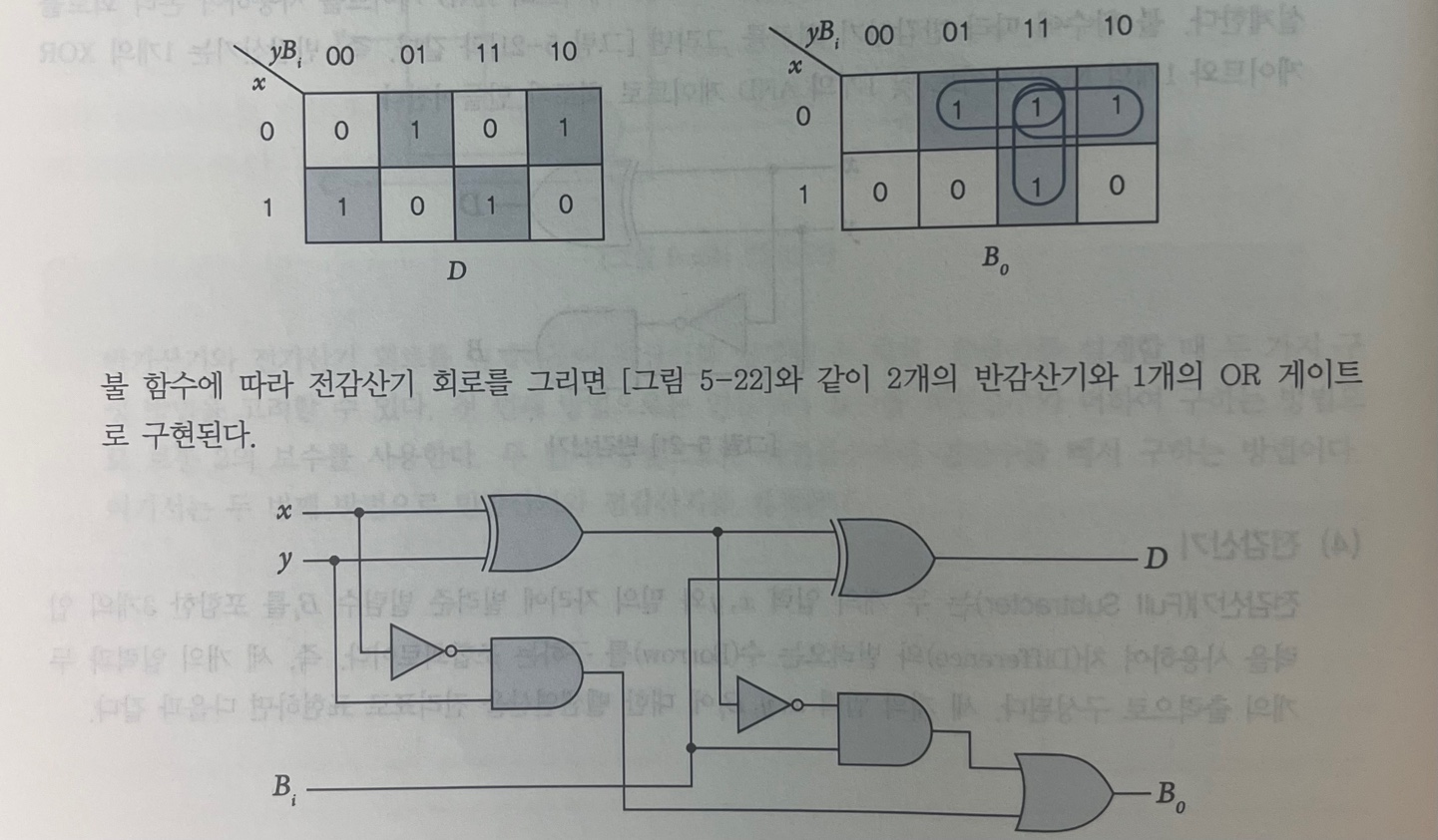
전감산기
Full subtracter
: 차와 빌려오는 수를 구하는 조합회로
- 입력 값 : 두 개의 입력 x,y 와 밑의 자리에 빌려준 빌림수Bi를 포함한 3개
- 세개의 입력과 두 개의 출력으로 구성
D = x'y'Bi + x'yBi' + xyBi = x ⊕ y ⊕ Bi Bo = x'y'Bi + x'yBi' + x'yBi + xyBi = x'Bi + x'y + yBi = x'(Bi ⊕ y)