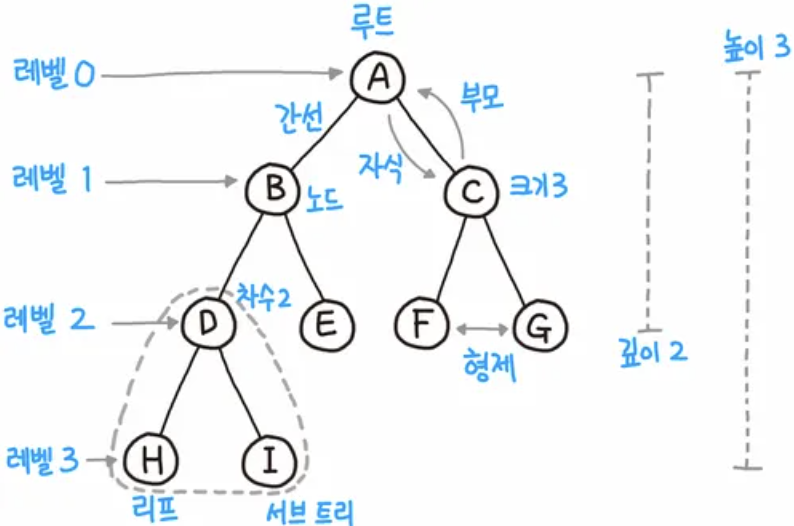
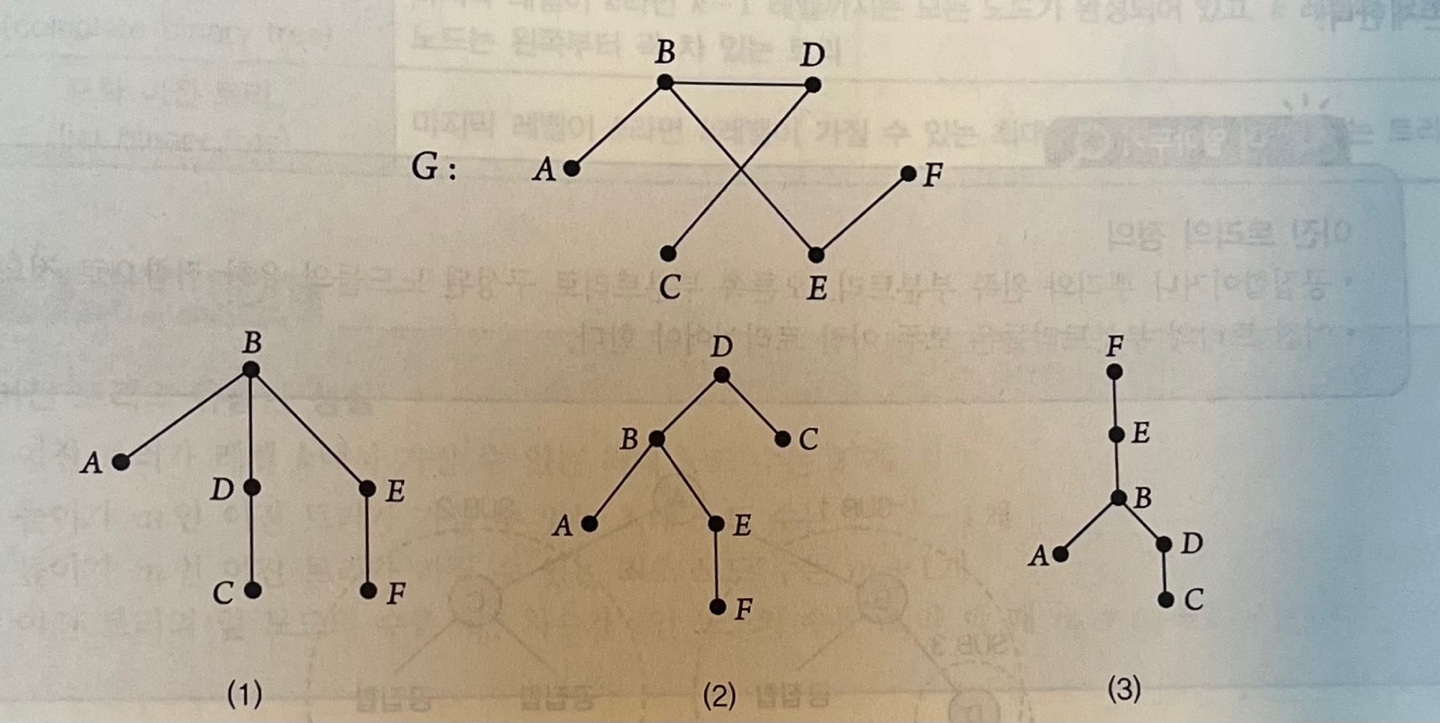
트리 Tree
: 그래프의 특별한 형태로서 회로(Cycle)가 없는 연결 무향(방향X) 그래프
트리의 응용 분야
최적화 문제의 해결
알고리즘(데이터 구조 및 정렬)
분자구조식 설계와 화학 결합의 표시 및 유전학
언어들 간의 번역, 언어학
자료의 탐색, 정렬, 데이터베이스 구성
사회과학(조직의 분류에 있어서의 구조)트리의 구조
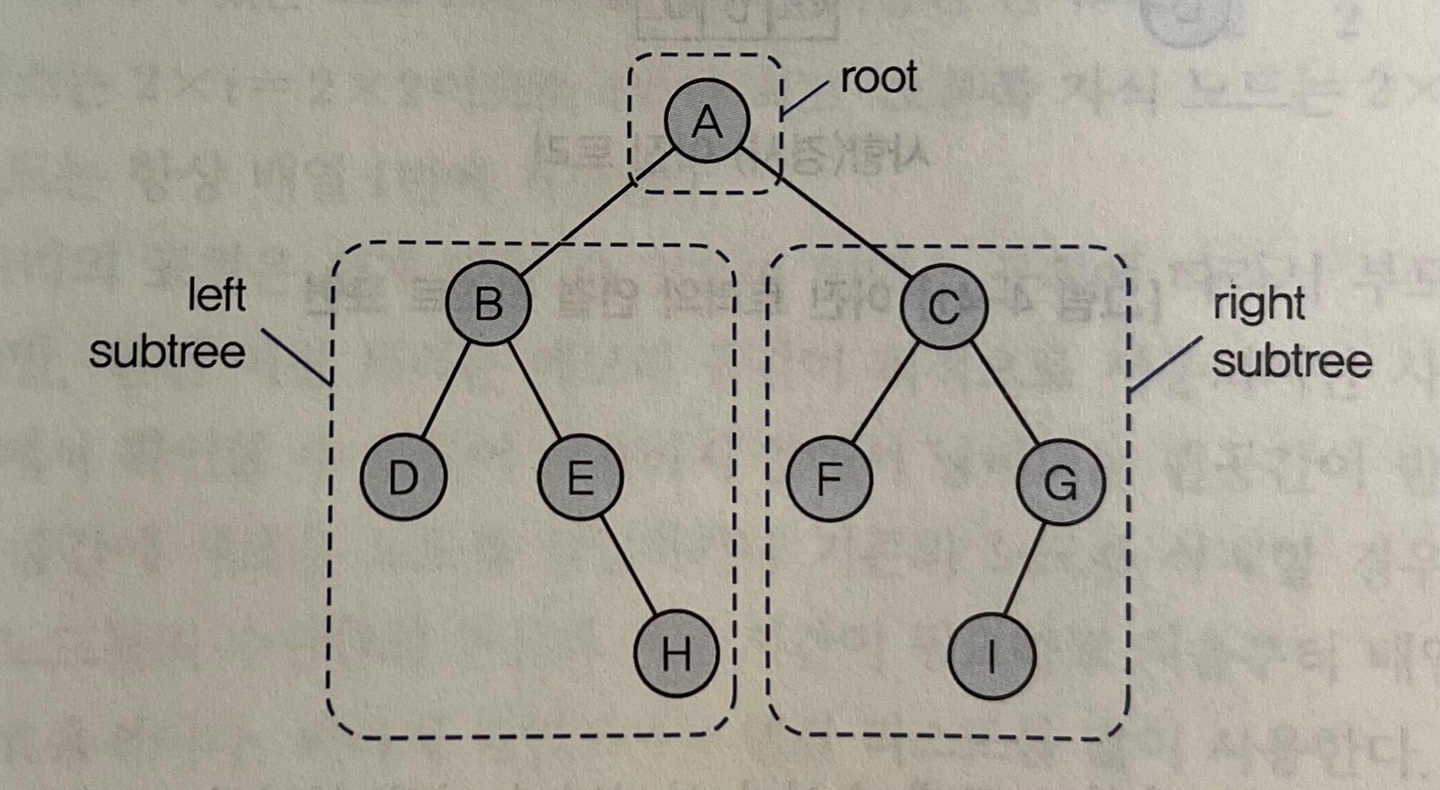
하나 이상의
노드(node)로 구성된 유한 집합
- 특별히 지정된 노드인 루트(root)
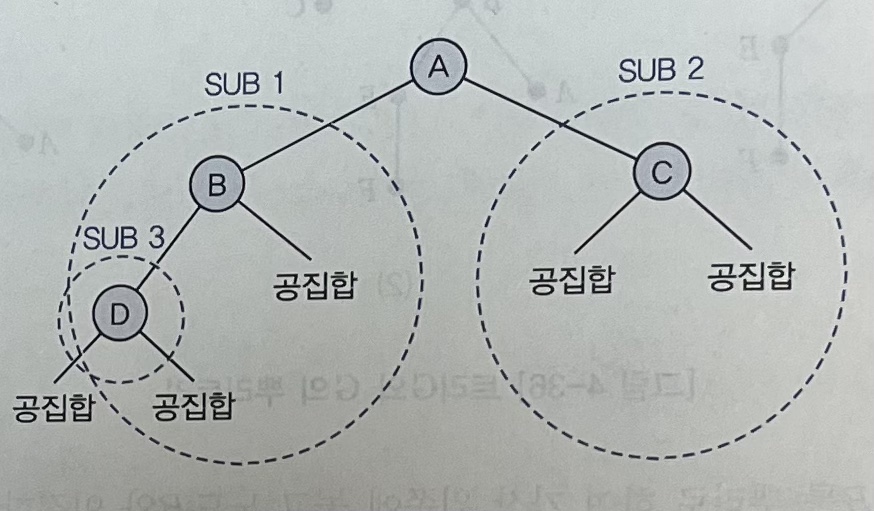
- 나머지 노드들 : 각각 트리이면서 연결되지 않는 트리들 => 서브트리(부분트리)가 된다.
노드(node) : 트리를 구성하는 개체 루트(root) : 트리의 시작 노드 / 통상 특정 노드를 지정 차수(degree) : 어떤 노드의 자식 노드의 개수 레벨(level) : 루트 = 레벨 0(또는 1)로 지정하고 하위로 갈수록 레벨 + 1 단말노드(=잎, terminal node) : 자식 노드를 가지지 않는 노드 자식노드(childre node) : 어떤 노드에 직접 연결된 하위 노드 부모노드(parent node) : 어떤 노드에 직접 연결된 상위 노드 형제노드(sibling node) : 동일한 부모 노드를 갖는 노드 중간노드(internal node) : 루트도 아니고 단말노드도 아닌 노드 조상(ancestor) : 루트로부터 어떤 노드에 이르는 경로상의 모든 노드 자손(descendant) : 어떤 노드에서 모든 단말노드에 이르는 경로상의 모든 노드 높이(height) : 트리의 최대 레벨 숲(forest) : 루트를 제거했을 때 발생하는 하위 트리n개의 노드를 가진 트리는 n-1개의 연결선을 가진다.
최소 신장 트리 MST
minimum spanning tree
: 트리를 구성하는 간선들의 비용(가중치) 합이 최소가 되는 신장 트리
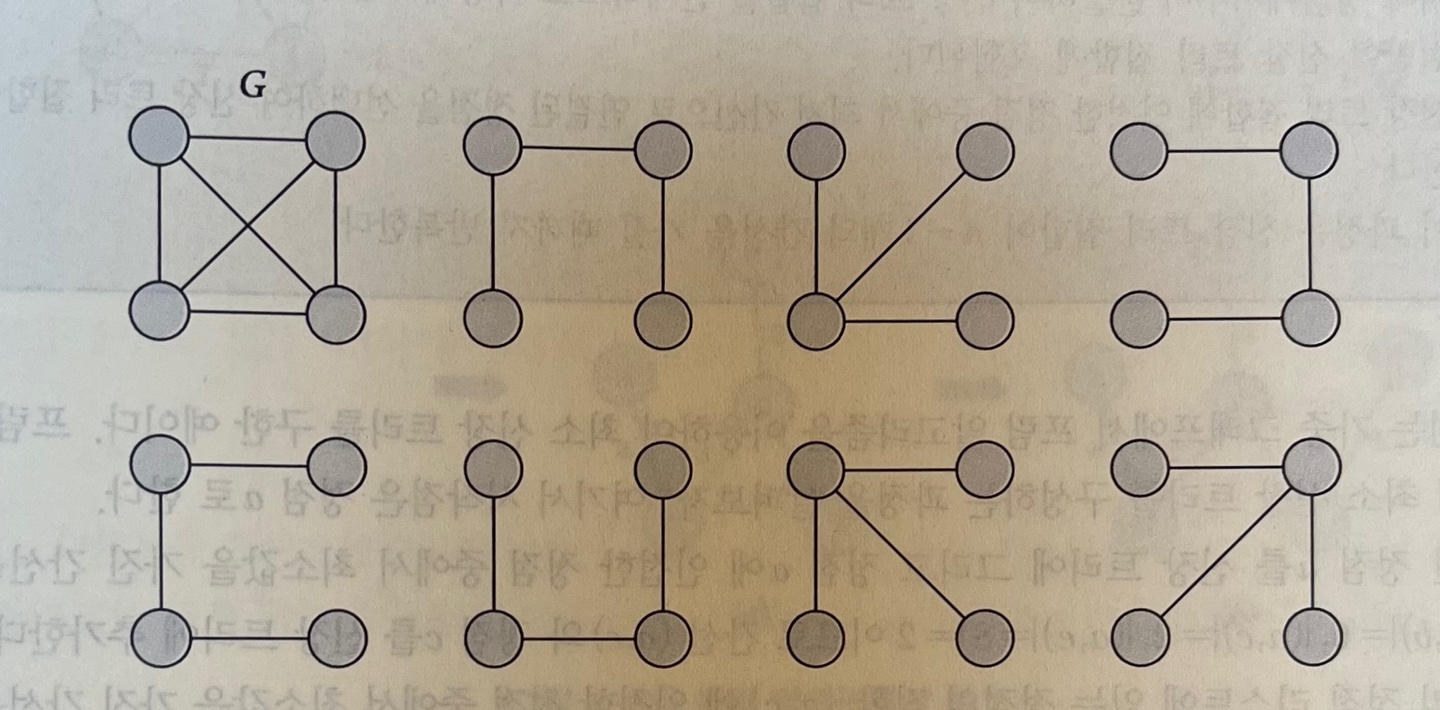
신장 트리(spanning tree, 생성 트리) : 어떤 그래프 G에서 모든 노드들을 포함하는 트리신장트리의 비용을 최소로 만드는 것은 실제 응용 분야에서 경제적이나 효율성을 고려할 때 매우 중요한 문제가 된다.
- 가중치가 부여된 무방향 그래프
G = <V,E>에서만 최소 비용 신장 트리를 만들 수 있으며 이때n - 1 (n=|V|)개의 간선만 사용한다.
=> 사이클을 생성하는 간선은 사용할 수 없음.
그래프 G와 G의 신장 트리들
최소 신장 트리를 찾아내는 알고리즘
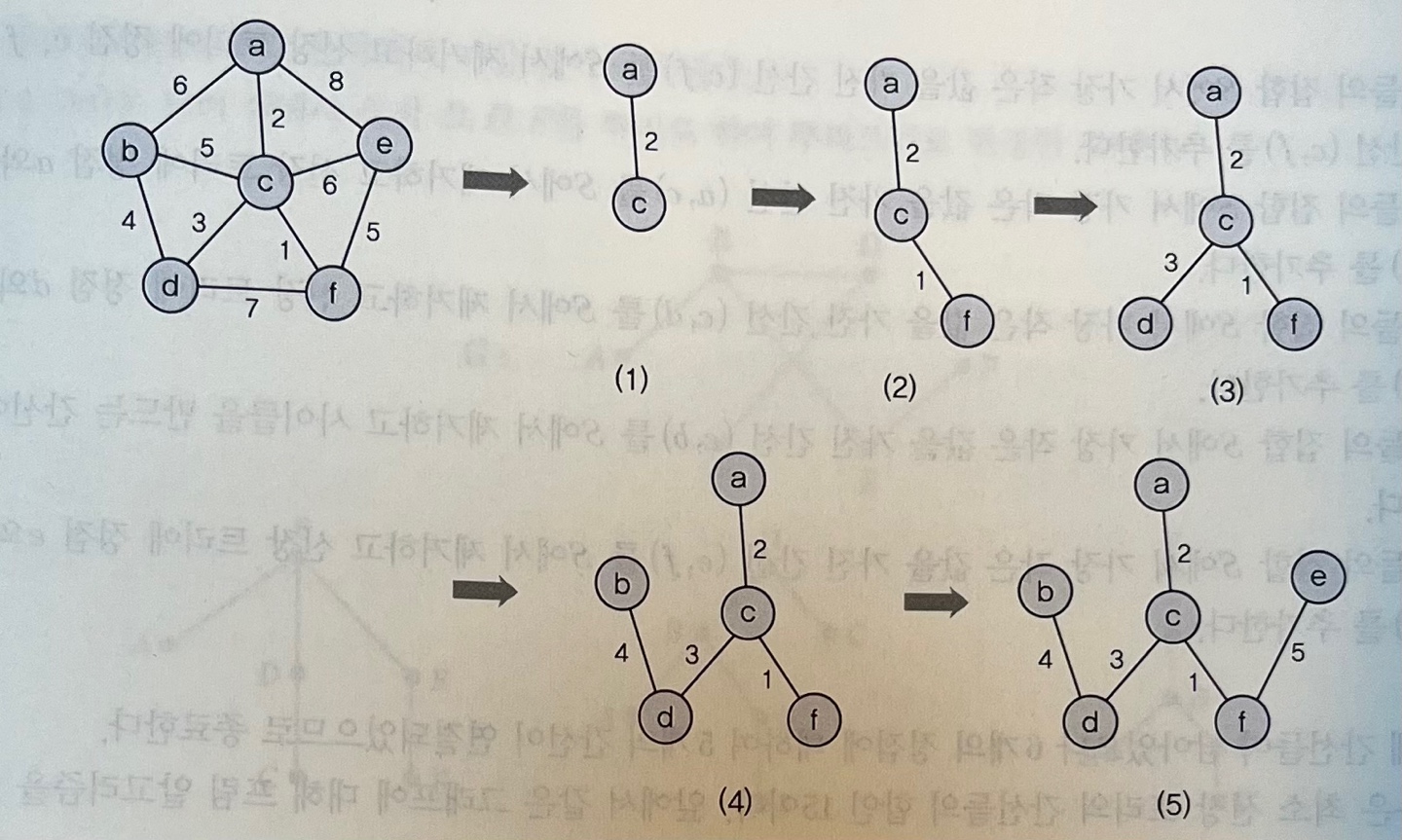
프림 알고리즘
Prim algorithm
- 임의의 정점을 시작점으로 하고 이 정점으로부터 연결된 간선들의 가중치를 비교 - 그 중 가장 작은 값은 가진 간선을 선택, 이 간선과 연결된 정점을 신장 트리에 추가 - 신장 트리에 있는 정점들 중 가장 작은 값을 가진 간선이 연결된 정점을 신장 트리에 추가이 방법을 신장 트리 집합이 n - 1개의 간선을 가질 때까지 반복하여 최소 비용 신장 트리 완성한다.
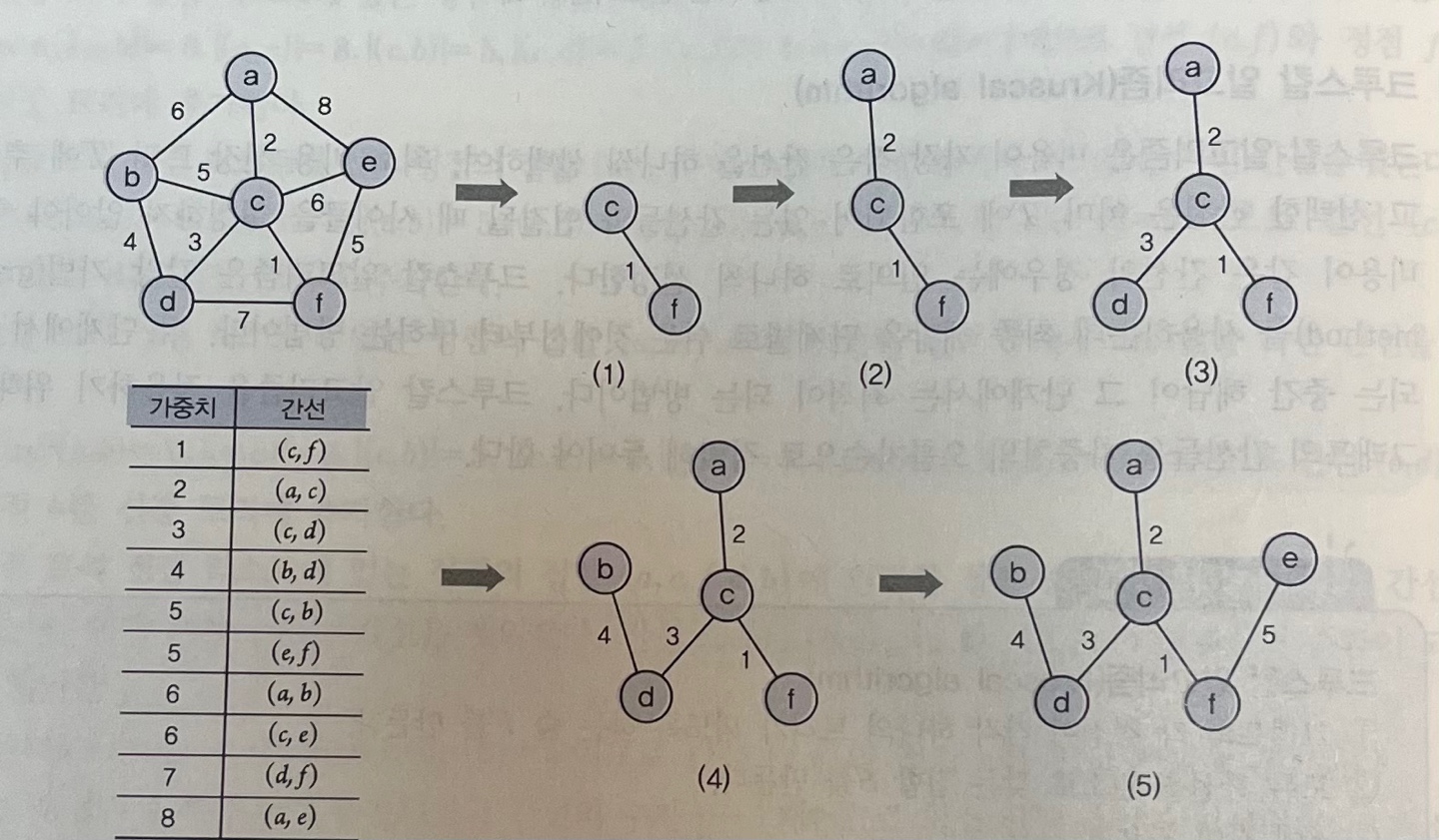
크루스칼 알고리즘
Kruscal algorithm
: 갈망 기법을 사용하는데 최종 해답을 단계별로 쉬운 것에서 구하는 방법
- 각 단계에서 생성되는 중간 해답이 그 단계에서는 최적이 되는 방법
- 그래프의 간선들을
가중치의 오름차순으로 정렬해 두어야 함.- 비용이 가장 작은 간선을 하나씩 선택하여, 최소 비용 신장 트리 T에 추가 (선택한 간선은 이미 T에 포함되어 있는 간선들과 연결될 떄 사이클을 형성하지 않아야함) - 비용이 같은 간선의 경우 임의로 하나씩 선정
뿌리트리
root tree
: 트리의 노드 중 하나가 루트로 지정된 트리
- 뿌리는 트리의 가장 위쪽에 위치함.
- 뿌리 이외의 나머지 노드들은 뿌리 밑에 계층적으로 놓임.
- 뿌리가 가장 상위에 있고 뿌리 외에 나머지 정점들은 뿌리로부터 도달하는 경로가 유일하게 존재
- 방향 트리(directed tree) : 뿌리를 제외한 모든 노드들이 오직 하나의 선행자만 갖고 있는 트리
각 노드의 후속자들은 통상 왼쪽부터 순서화된다.
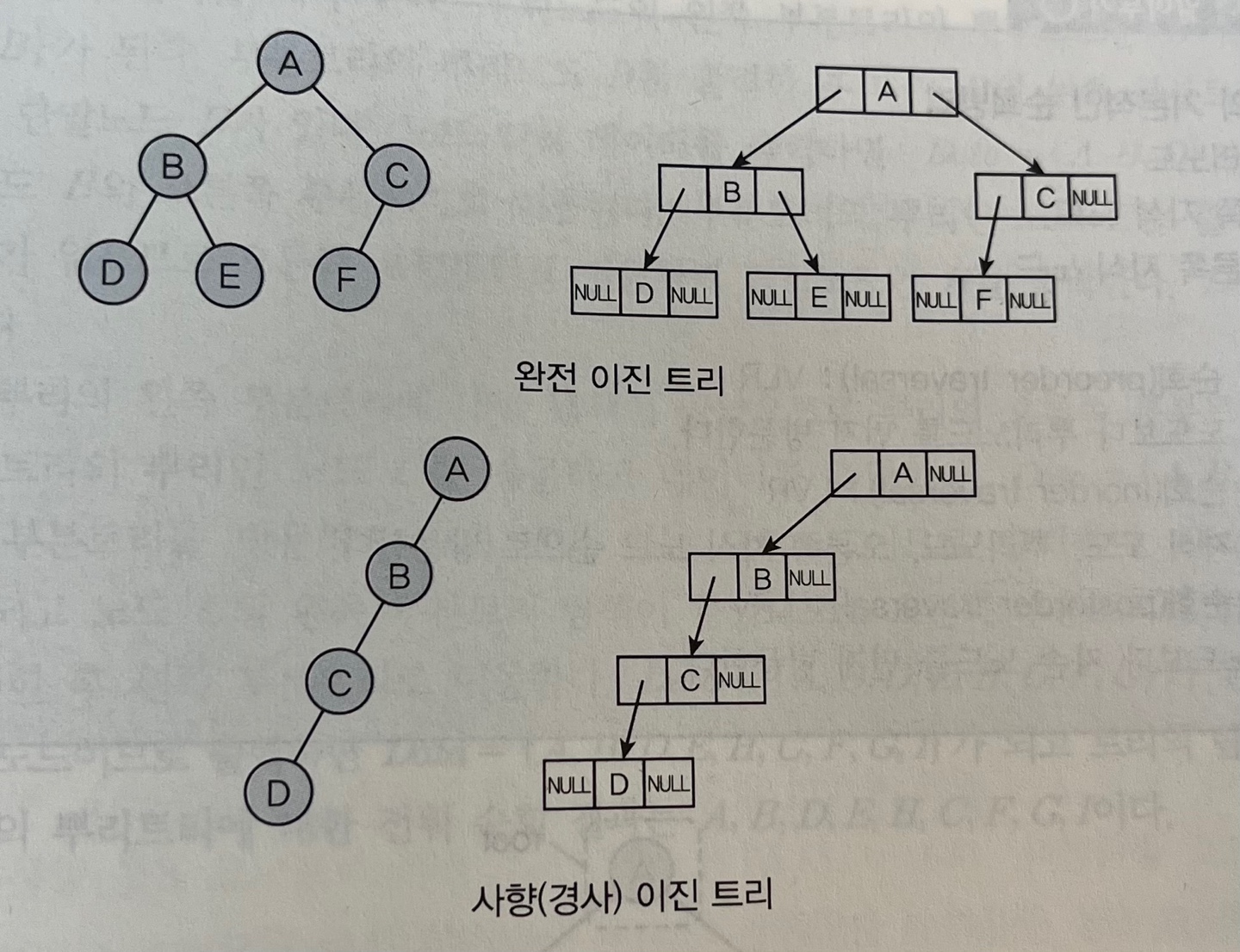
이진 트리
binary tree
: 뿌리트리에서 자식노드가 2개 이하인 트리 (= 최대 2개, 모든 노드의 차수가 2 이하)
- 0개 이상의 노드들로 이루어진 유한 집합
- 공집합이거나 모든 노드들은 뿌리의 왼쪽 부분트리와 오른쪽 부분트리로 구성된다.
- 모든 노드가 2개의 부분트리를 가지고 있는 트리 (부분트리는 공집합일 수 있음)
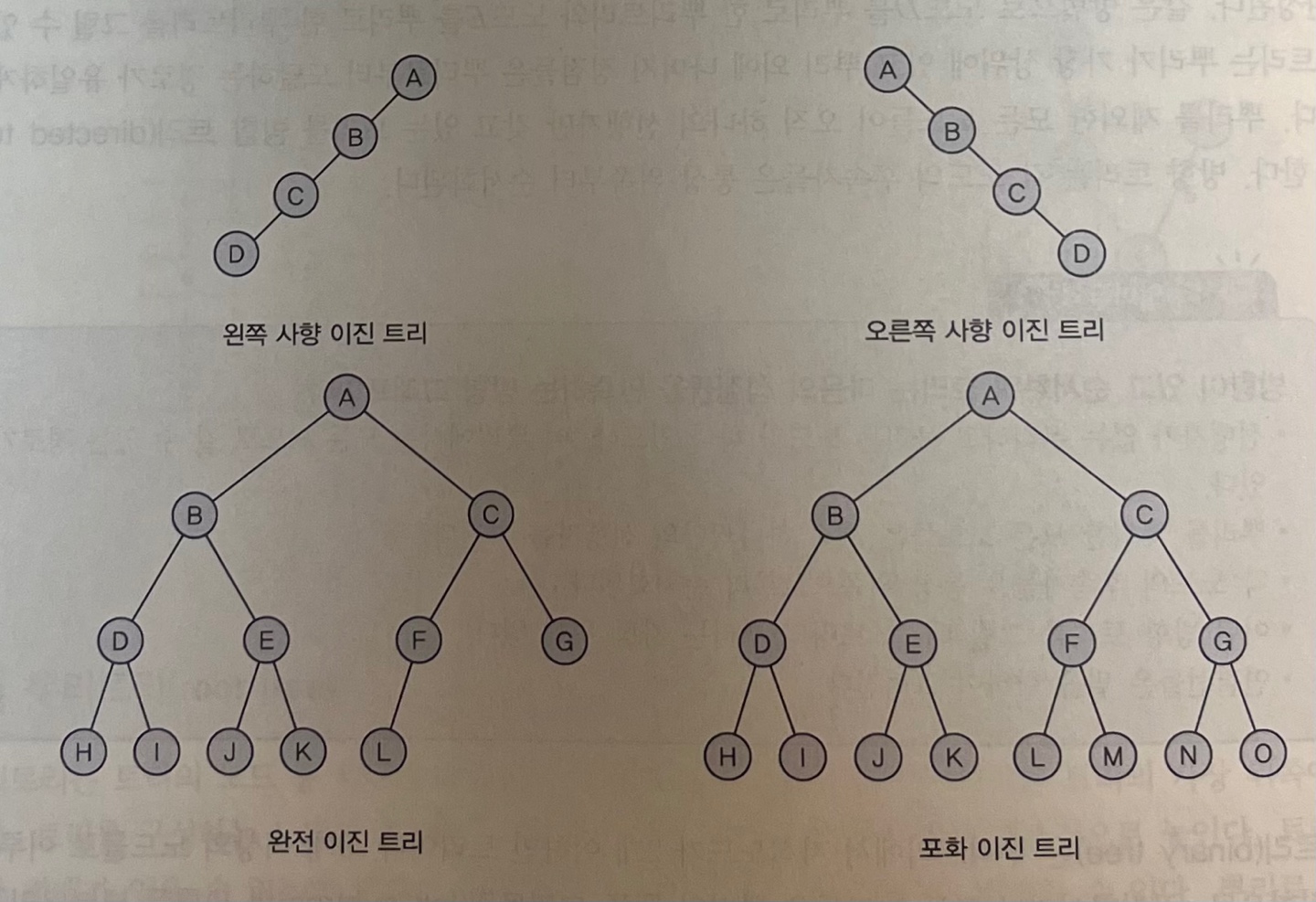
이진 트리의 유형 - 경사(사향) 이진 트리 : 모든 노드들이 한쪽으로만 존재하는 트리. - 완전 이진 트리 : 마지막 레벨 = k → k - 1 레벨까지는 모든 노드가 완성. k레벨의 모든 노드는 왼쪽부터 꽉 차 있는 트리 - 포화 이진 트리 : 마지막 레벨 = k → k레벨이 가질 수 있는 최대 노드를 모두 가지고 있는 트리
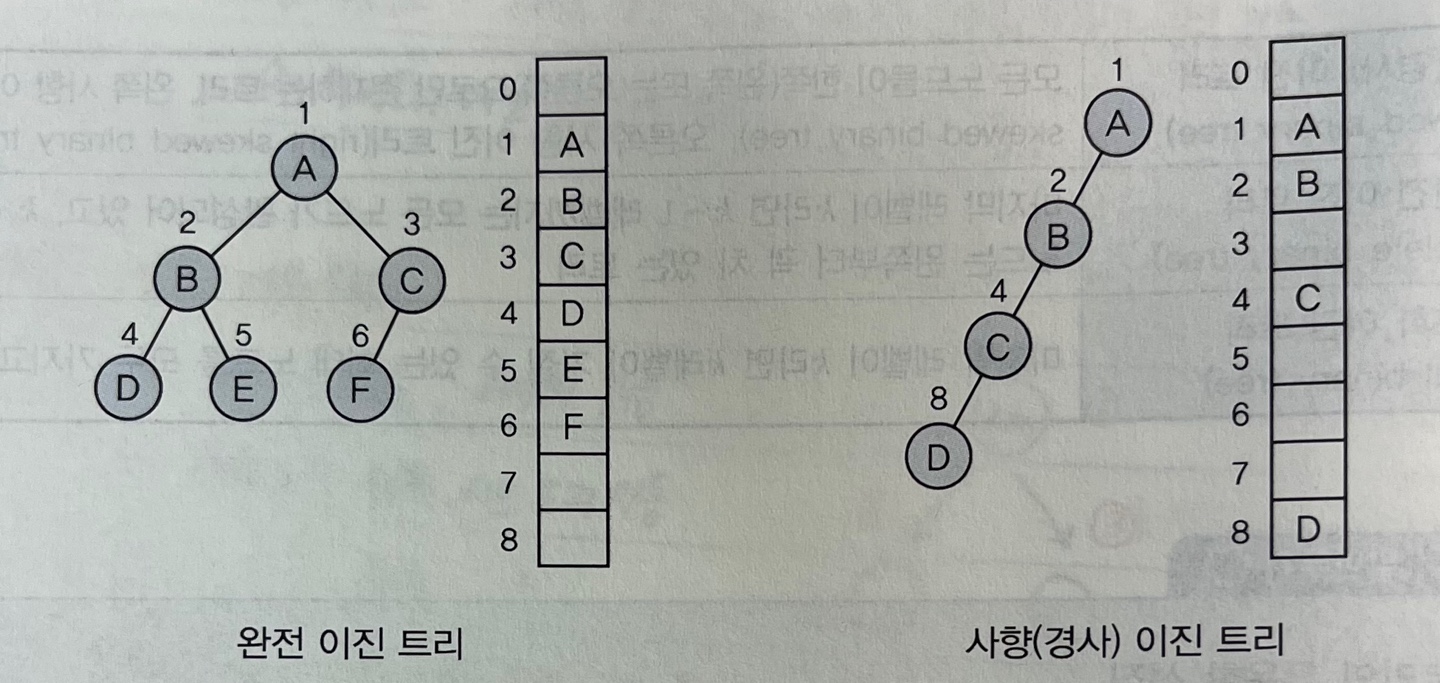
- 이진트리는 배열(1차원 배열)과 연결 리스트를 이용하여 표현할 수 있다.
이때 뿌리 아래 노드들의 위치를 정할 때 왼쪽 자식과 오른쪽 자식을 구분할 수 있어야 한다.- 저장된 배열 인덱스의 일정한 규칙
형제 노드 중 왼쪽 노드 인덱스 순서가 오른쪽 노드보다 빠르다.
노드 번호는 1부터 시작하며 인덱스 0번은 비워둔다.루트노드(뿌리노드) = 1 (n > 0) 노드 i의 부모 노드 인덱스 = i / 2 (i > 1) 노드 i의 왼쪽 자식 노드 인덱스 = i X 2 (i X 2 <= n) 노드 i의 오른쪽 자식 노드 인덱스 = i X 2 + 1 (i X 2 + 1 <= n)
- 이진 트리의 배열 표현 완전 이진 트리는 메모리 공간이 최적으로 사용되지만 사향 이진 트리는 낭비되는 빈공간이 발생한다. 배열로 표현할 경우 새로운 노드 삽입 혹은 삭제가 있을 시 노드의 이동이 필요하고 배열 공간을 미리 선언해놔야하기 때문에 비효율적이다.
- 이진 트리의 연결 리스트 표현 포인터를 이용해 부모 노드가 자식 노드를 가르키게 하는 방법이다. 하나의 노드 = 왼쪽 링크 필드 + 데이터 필드 + 오른쪽 링크 필드 ↑ 왼쪽 자식 노드 + 노드의 값 + 오른쪽 자식 노드 자식 노드가 없을 경우 링크 필드 = NULL
이진트리의 유용한 성질
이진 트리가 레벨 k에서 가질 수 있는 최대 노드 수 : 2^k 높이가 m인 이진 트리가 가질 수 있는 최대 노드 수 : 2^m+1 -1 높이가 m인 이진 트리가 가질 수 있는 최소 노드 수 : m + 1 이진 트리의 단말 노드의 수를 n0, 차수가 2인 노드의 수 n2 : n0 = n2 + 1
정렬과 탐색
순서 트리
Ordered Tree
: 각 자식 노드에 순서가 부여되어 저장 위치가 고정되는 트리
- 형제 노드들 간에 순서가 정해져 있음
활용 허프만부호트리, 구문해석의 구문트리, 결정 트리(계산의 결정과정 나타냄)순서가 있는 데이터들을 삽입, 삭제, 수정, 정렬, 탐색 등을 효율적으로 행할 수 있는 구조인 이진트리를 순서트리에 많이 사용한다.
탐색
traversal
: 트리의 노드들을 체계적으로 방문
- 트리에서 가장 빈번하게 하는 연산
- 각 노드를 꼭 한번씩만 방문함.
- 탐색 결과 : 각 노드에 들어 있는 데이터를 차례대로 나열한다.
이진 탐색 트리
: 노드가 가지는 데이터의 내용에 대한 기준에 따라 노드의위치를 탐색할 수 있는 트리
구성 - 임의의 정점의 왼쪽 부분트리 : 해당 정점보다 작은 값 배정 - 임의의 정점의 오른쪽 부분트리 : 해당 정점보다 큰 값 배정트리 순회(tree traversal) : 트리의 각 노드를 체계적인 방법으로 방문하는 과정
- 뿌리부터 탐색 시작
- 하나도 빠트리지 않고 중복없이 정확히 한번만 방문해야한다.
노드를 방문하는 순서에 따라 세가지로 나뉜다.
탐색의 방식
전위 순회 VLR
preorder traversal
: 자손 노드보다 뿌리 노드를 먼저 방문
1) 뿌리 노드 방문 → 데이터 출력 2) 트리의 왼쪽 부분 트리 방문 3) 트리의 오른쪽 부분 트리 방문
- 수식 표현 : 전순위 표기(prefix)
중위 순회 LVR
inorder traversal
: 왼쪽 자식 노드, 뿌리노드, 오른쪽 자식 노드 순으로 방문
1) 트리의 왼쪽 부분 트리 방문 2) 뿌리 노드 방문 → 데이터 출력 3) 트리의 오른쪽 부분 트리 방문
- 수식 표현 : 중순위 표기(infix)
후위 순회 LRV
postorder traversal
: 뿌리 노드보다 자손 노드 먼저 방문
1) 트리의 왼쪽 부분 트리 방문 2) 트리의 오른쪽 부분 트리 방문 3) 뿌리 노드 방문 → 데이터 출력
- 수식 표현 : 후순위 표기(postfix)
전위 순회 결과 : A B D E H C F G I 중위 순회 결과 : D B E H A F C I G 후위 순회 결과 : D H E B F I G C A 서브트리로 쪼개어 순서를 정하는 방법을 터득해야한다.
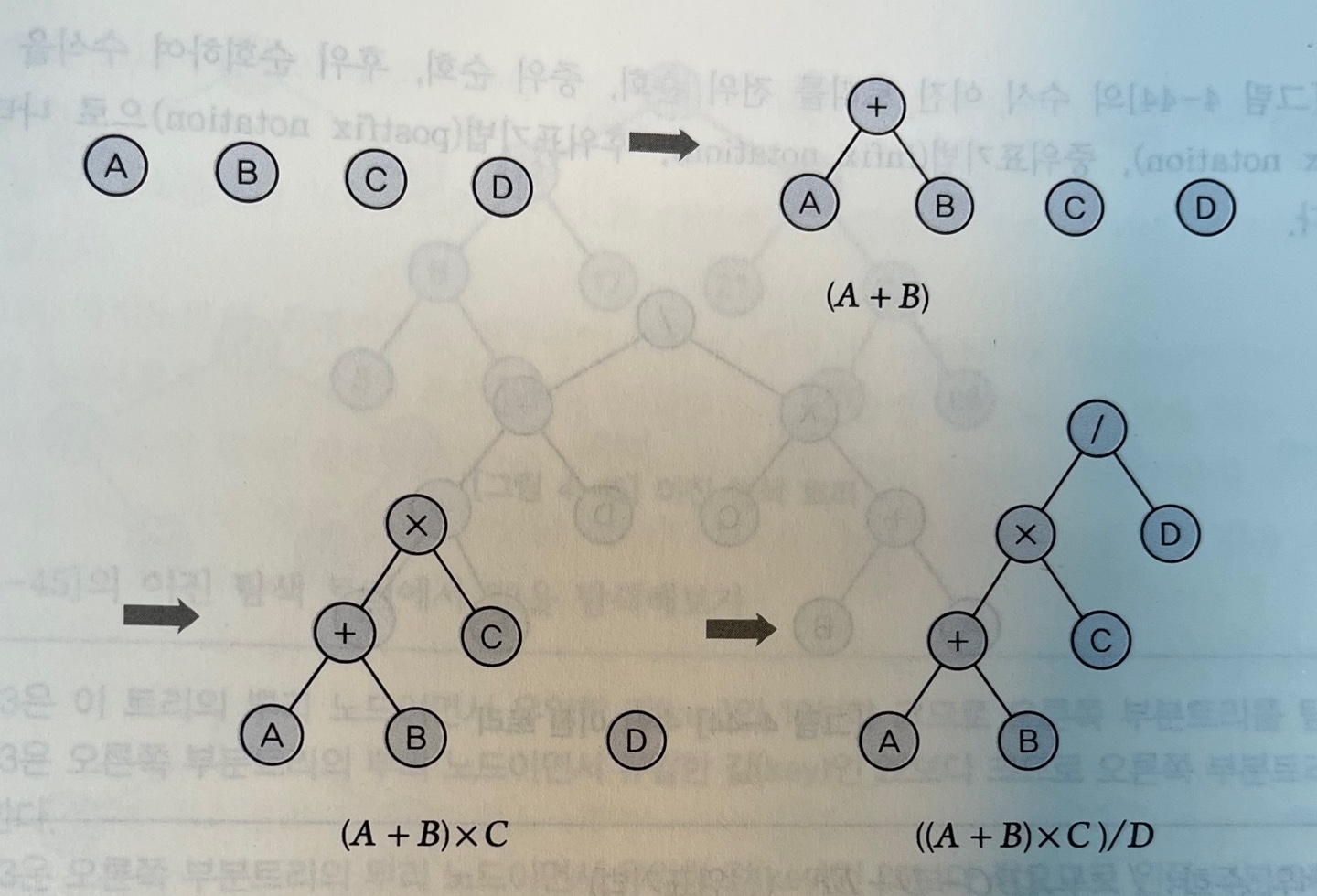
이진 트리 수식을 피연산자와 연산자를 구분하여 표현하는 방법으로 사용되기도 한다.
- 피연산자 : 단말노드
- 연산자 : 비단말노드 (루트 ~ 중간노드)
Ex : ((A + B) X C) / D 의 수식 이진 트리 만드는 법 1) 수식에서 연산자와 피연산자를 먼저 단말 노드로 표현 2) 피연산자들을 수식에 따라 연산자 노드에 연결하는 작업을 계속하면 수식이 완성됨전위 표기법 : 연산자 | 두 피연산자 중위 표기법 : 피연산자 | 연산자 | 피연산자 후위 표기법 : 두 피연산자 | 연산자표현된 수식 전위 표기법 = /X+ABCD 후위 표기법 = AB+CXD/
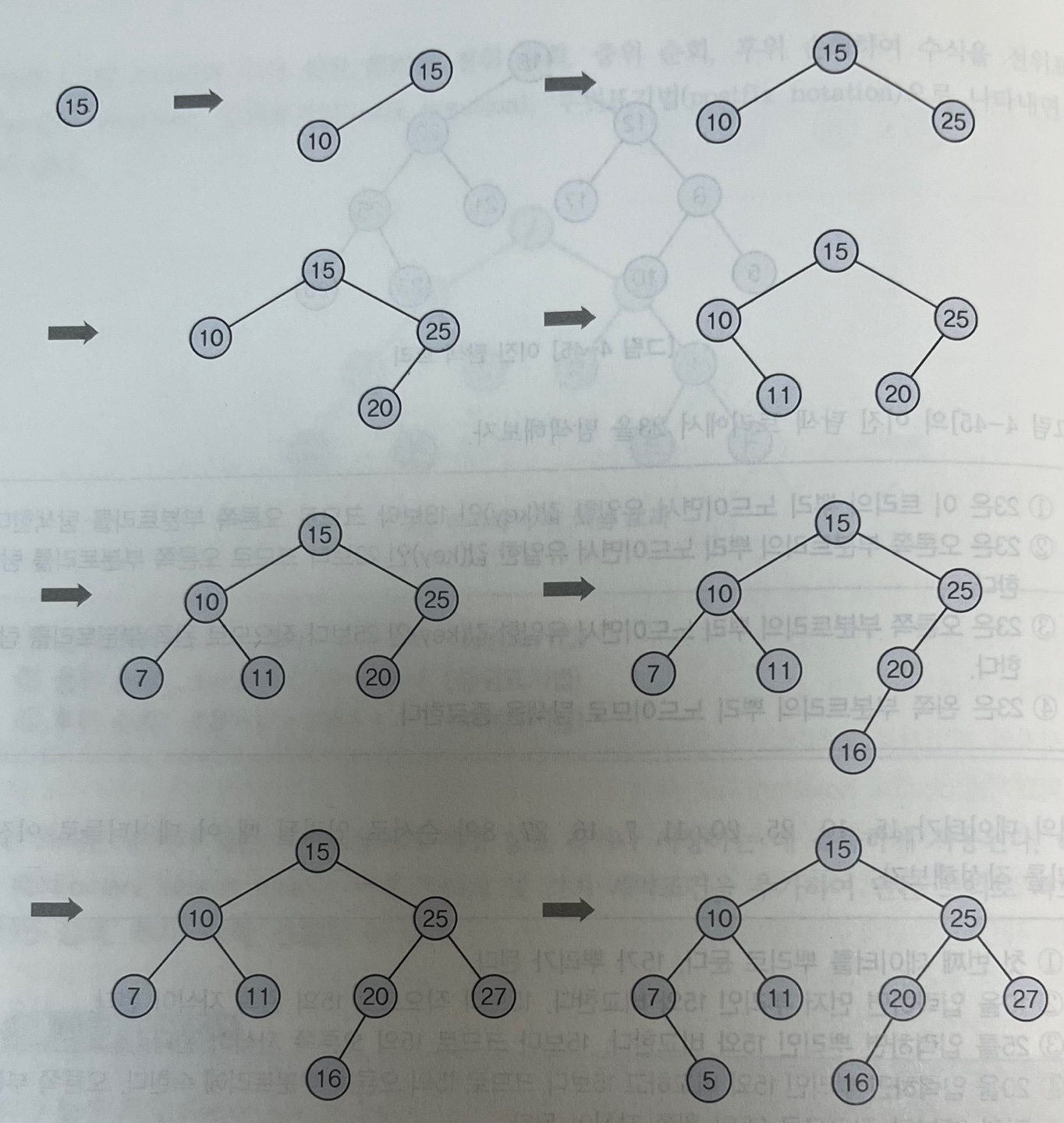
EX) 9개의 데이터 15,10,25,20,11,7,16,27,8 순서로 입력될 때 이 데이터들로 이진 탐색 트리를 작성하는 과정이진 탐색 트리 구현을 위한 규칙
1) 트리에서 탐색되는 모든 원소는 서로 다른 유일한 키값을 갖는다. 2) 왼쪽 서브 트리 원소 < 뿌리 값 (보다 작거나 앞선 순서 가짐) 2) 오른쪽 서브 트리 원소 > 뿌리 값 (보다 크거나 뒤의 순서 가짐)
정렬
sorting
데이터를 어떤 순서로 나열하는 것. (오름차순 / 내림차순)
힙 정렬
: 정렬하고자 하는 데이터를 새로운 힙에 삽입하여 최대 힙 혹은 최소 힙으로 완성한 후 하나씩 삭제하며 정렬된 순서대로 데이터들을 빼 정렬하는 것
1) 첫 번째 원소 두 번째 원소 순서대로 연결 후 위치 설정 2) 힙은 완전이진트리이므로 세번째 원소를 일단 마지막 위치에 놓고 난 후 부모노드와 크기 비교 후 위치 설정 3) 이 과정을 계속 반복한다.최대 힙과 최소 힙에 대해 힙이 완전히 비어있는 상태가 될때까지 삭제연산을 반복하여 주어진 원소들을 오름차순과 내림차순으로 정렬한 결과를 얻는다.
삭제 연산이란최대 값이라면 최대 힙에서 최대값을 가진 요소를 삭제하는 것 먼저 뿌리노드의 값을 지우고 힙을 재구성한다. 힙의 재구성 : 힙의 성질을 만족하기 위해 부모와 자식 노드를 교환하는 과정 1) 뿌리 노드 삭제 빈자리에 힙의 마지막 노드 이동 2) 뿌리노드가 된 노드와 자식노드와 비교해 교환 3) 힙이 빈 상태가 될 때까지 반복
힙(heap)
: 완전이진트리를 기본으로 한 자료구조로서 최댓값 및 최소값을 찾아내는 연산을 빠르게 한다.
- 노드 값의 대소관계는 부모노드와 자식노드 사이에만 성립, 형제 사이 대소관계는 정해지지 않음.
- 최대 힙 : 부모노드 값 > 자식노드 값 뿌리노드 = 모든 노드 중 최댓값 - 최소 힙 : 부모노드 값 < 자식노드 값 뿌리노드 = 모든 노드 중 최소값
순서트리 활용 - 허프만 코드 트리
Huffman code tree
허프만 코드 : 데이터를 효율적으로 압축하는데 사용하는 방법, 탐욕 알고리즘 중 하나
문자 빈도수를 이용해 허프만 코드 트리를 만들고 허프만 코드 트리에서 허프만 코드를 생성한다.
=> 이때 허프만 코드 트리는 최대 힙임
데이터 압축(Data Compression) : 파일의 크기를 줄인다.
- 문자의 발생 빈도에 따라 7비트 길이의 아스키코드의 크기를 조절한다.
발생 빈도가 높은 문자 : 적은 비트 할당
발생 빈도가 낮은 문자 : 많은 비트 할당
=> 파일의 용량을 줄인다.
허프만 알고리즘
1) 문자 발생 빈도를 값으로 하는 노드 만듬 2) 노드들을 크기 순서로 나열 3) 발생 빈도가 가장 낮은 두 문자의 노드를 선택해 하나의 이진 트리로 연결 ❗️ 뿌리노드 & 남은 노드 값을 비교해 낮은 두 문자를 계속 선택해 연결하는 방법 - 빈도수가 낮은 문자의 노드는 왼쪽에 빈도수가 높은 문자는 오른쪽에 놓는다. - 두 노드의 뿌리 : 두 문자 빈도의 합 - 문자들을 이진 트리로 연결하는 작업을 최우선하고 그 후에 부분 이진 트리들을 연결. (각각의 문자와 부분이진트리의 뿌리의 값이 동일한 경우 발생 가능하기 때문) 4) 이 과정을 모든 문자가 하나의 이진 트리로 만들어질 때까지 반복 5) 완성된 이진 트리의 왼쪽 노드 : 0, 오른쪽 노드 : 1 부여 + 뿌리부터 해당 문자까지 부여된 0 또는 1을 순서대로 나열하면 해당 문자의 허프만 코드가 된다.허프만 코드 생성시 고려해야할 사항
- 만들어진 코드는 다른 영문자의 코드의 접두어로 표현되지 않아야함. 제대로 만들면 접두어가 발생하지 않는다. Ex) a = 10 b = 101이면 a는 b의 접두어가 됨으로 허프만 코드 적합 X
순서트리 활용 - 결정 트리
decision tree
: 의사를 결정하는 규칙과 그에 따른 결과들을 트리 구조로 만든 의사 결정을 지원하는 도구의 일종
- 운용 과학 중 의사 결정 분석에서 목표에 가장 가까운 결과를 낼 수 있는 전략을 찾을때 이용함.
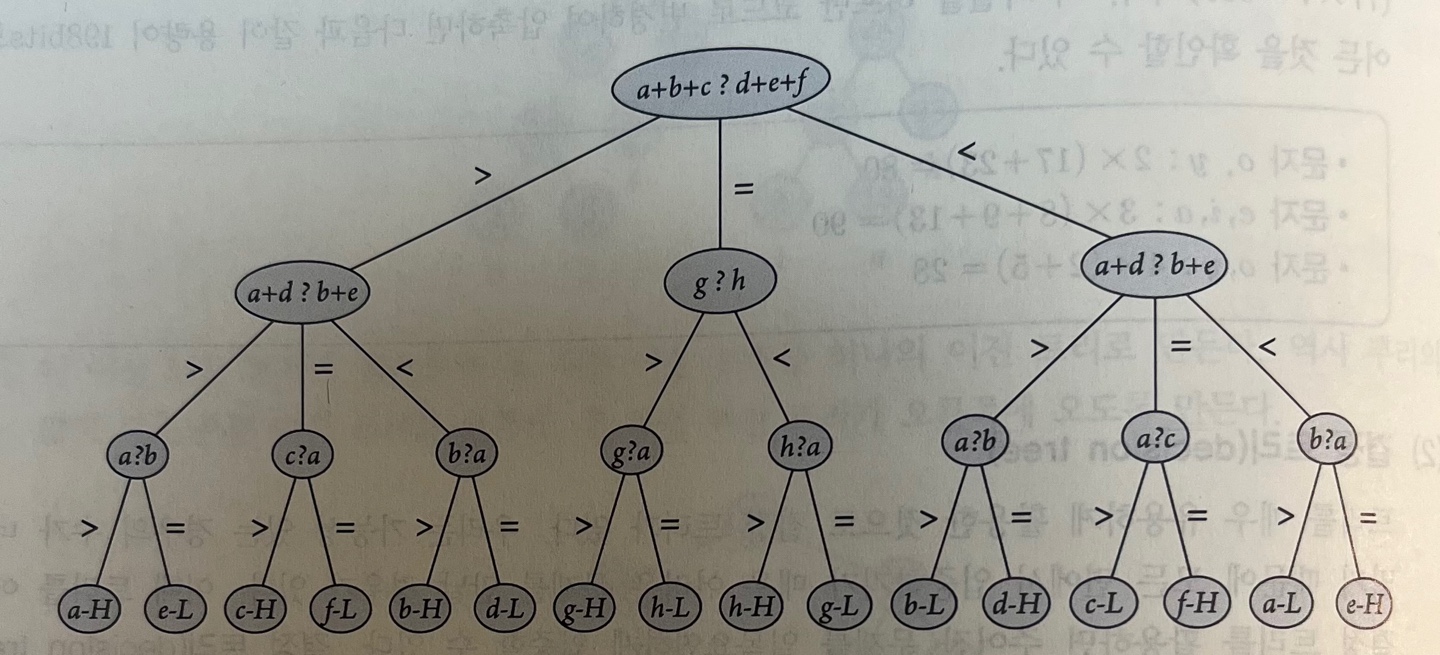
Ex) 8개의 동전 문제 (eight-coins problem)크기와 색이 똑같은 8개의 동전이 있는데 이 중 한 개는 무게가 다름 이 불량인 동전은 하나의 천칭 저울(무게가 같거나 크고 작은 것만 판단 가능한 저울)을 세 번만 사용하여 불량니 동전을 찾을 수 있다.
- 딱 3번 비교해서 찾음.
- 8개의 동전이 정상적인 동전보다 무겁나 가볍나에 대해서 비교한 결과가 16가지가 나온다.
L : 정상보다 가벼움 / H : 정상보다 무거움