알고리즘

: 어떤 문제를 해결하기 위해 수행하는 명령어들의 유한 집합으로 이루어진 절차나 방법

• 프로그램 개발의 기초 단계 (계획을 세우고 총괄하는 역할)
• 주어진 문제 해결을 위해 필요한 입력을 파악하고 입력을 처리하는 명령을 단계별로 나열하여 필요한 출력이 나오도록 한다.

알고리즘의 개발 단계

문제 정의 → 모델 고안 → 명세(세세한 사항) 작성 → 설계 → 검증 → 분석(복잡도 등) → 구현 → 테스트 → 문서화 

알고리즘 표현 방법

자연어

Natural language
: 우리가 일상생활에서 사용하는 언어로 알고리즘을 기술하는 것.

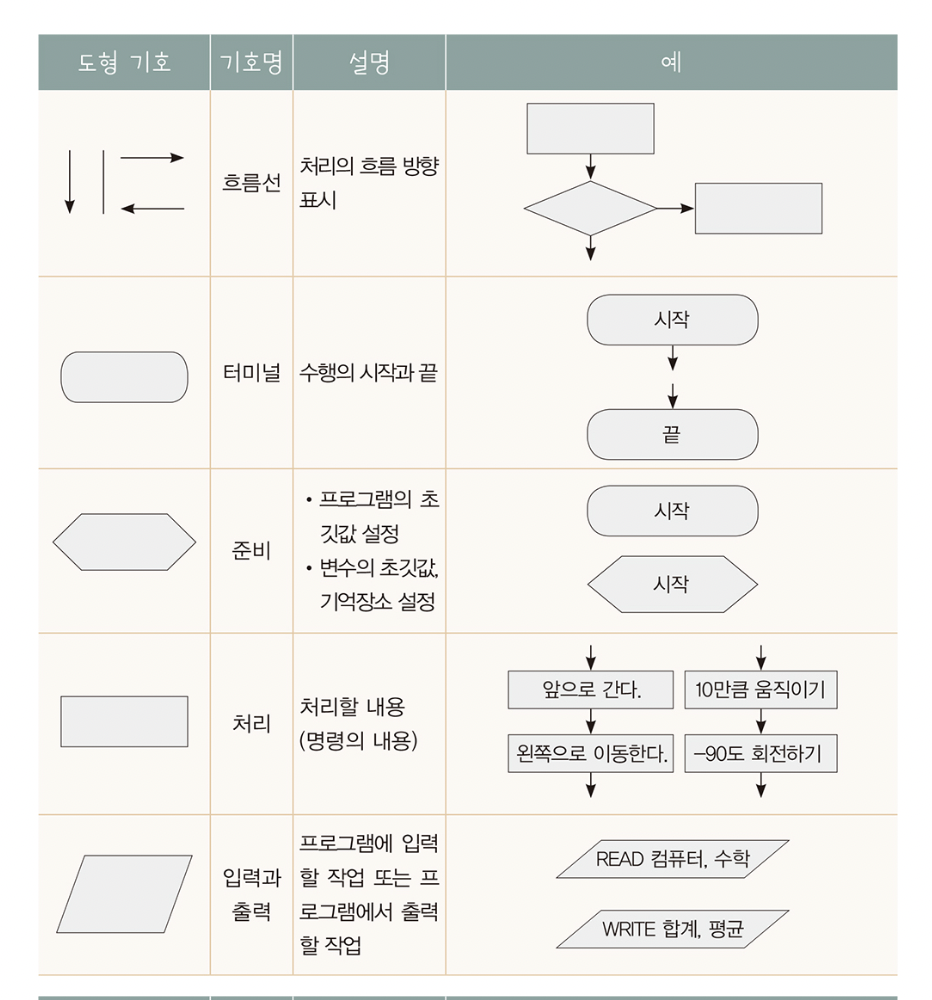
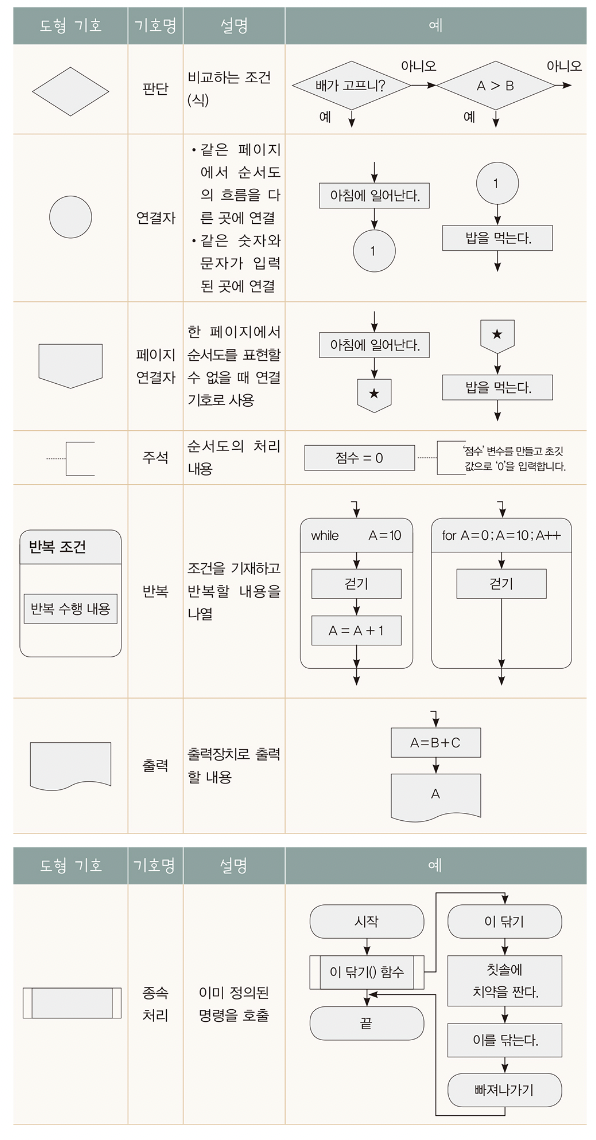
순서도

Flow chart
: 약속된 기호를 이용하여 알고리즘 표현한 것.

• 명령의 흐름을 명확히 나타내어 이해하기 쉽지만 프로그램이 큰 경우 적합하지 않음. 즉, 구조적 프로그램이 어렵다.
  

출처 : https://booksr.tistory.com/13

• 항상 시작과 종료가 포함되어야한다.

의사코드

Pseudo-code
: 컴퓨터 프로그램이나 알고리즘이 수행해야할 내용을 우리가 사용하는 언어로 간략히 서술해 놓은 것.

• 알고리즘 언어로 가장 많이 사용된다.
• ← : 대입연산자

프로그래밍 언어

Programming language

• 명령어의 의미가 명확하며, 즉시 컴퓨터로 수행할 수 있다는 장점

좋은 알고리즘의 특성

정확성, 확정성, 효율성, 입력, 출력, 유한성, 일반성

알고리즘의 효율성

: 문제를 해결하기 위한 알고리즘은 여러개 존재할 수 있다. 그러므로 어떤 알고리즘이 효율적인지 선택할 수 있는 일반적인 기준이 있다.

• 수행 시간, 수행에 필요한 메모리 용량, 자료의 종류, 프로그래머의 성향
• 여러 알고리즘 중 비용이 적게 드는 (= 수행시간 & 메모리 용량) 알고리즘을 찾기 위해서는 효율성 분석(Perfomance analysis)이 필요함.

효율성 분석

시간 복잡성(time complexity) 공간 복잡성(space complexity) 고려

• 입/출력 자료의 크기에 비례함.
• 하드웨어의 발달로 기억 장소에 대한 효율성 분석은 비중이 적다.

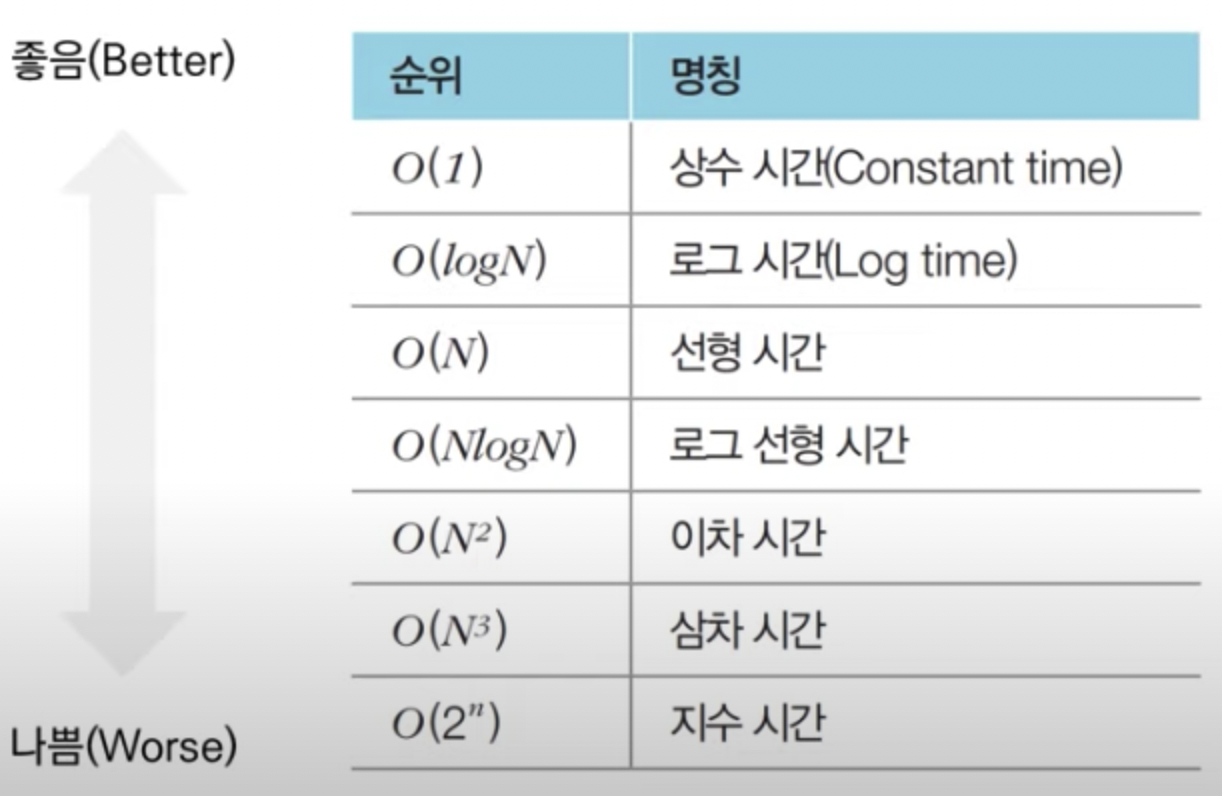
알고리즘의 복잡성

수행 시간이 짧거나 기억 공간을 적게 사용하는 알고리즘이 효율적인 알고리즘. 즉, 복잡도가 낮을수록 효율적이다.

• 일반적으로 복잡도는 시간 복잡도를 의미한다.
  
• 빅오(Big-Oh) 시간 복잡도 그래프

재귀 함수의 복잡성

: recursive function 자기 자신을 다시 호출하는 함수

O(n)

탐색 알고리즘

순차 탐색 알고리즘

: 원소들을 처음부터 하나씩 비교하여 탐색하는 알고리즘

• 효율적이진 않지만 효과적인 방법이다.
• 모든 원소들을 조사하는 탐색 : 선형 탐색(Linear search)

최상의 경우 : 가장 빠른 경우, 한번 탐색하고 종료. 수행 횟수 f(1)= 1
최악의 경우 : 가장 늦는 경우, 탐색 대상의 수인 n번만큼 탐색. f(n) = n
평균적인 경우 : f(n) = 3/4 n 
복잡도 : 최악의 경우 - O(n)

이진 탐색 알고리즘

: 원소들을 반으로 나누어 기준을 정하고 그 기준과 특정 원소를 비교하여 특정 원가 속하는 영역에 대해 탐색을 반복하는 방법으로 탐색 범위를 좁혀가는 알고리즘

분할 정복 알고리즘

: 원소 전체 집합을 찾으려는 원소와 비교하여 부분집합으로 나누어 찾는 알고리즘

• 1) 원소들이 이미 정렬되어 있을 때
  처음부터 찾을 필요 없이 중간의 원소와 비교해 그보다 작을 때는 그 원소의 왼쪽 원소들 중에서 클때는 그 반대로 탐색한다.

수행 횟수에 따른 배열의 크기 : 탐색해야 할 배열의 크기가 1일 때 알고리즘 수행이 끝난다.
수행 횟수 1 → 배열의 크기 n | 2 → n/2
복잡도 : O(log2n)

이진 탐색 트리

• 처음 배열의 중간 원소를 루트로 놓고 각 서브 트리의 루트는 둘로 나누어진 부분집합들의 중간 원소들로 만들어진다.
• 이진 탐색 알고리즘의 과정을 나타낼 수 있음.
• 루트로부터 노드로 가는 경로는 이진 탐색 트리 알고리즘의 비교 횟수와 동일함.

최악의 경우 : 비교 횟수 - 트리의 깊이 (log2n)이 된다.

정렬 알고리즘

정렬(Sort) : 주어진 파일 또는 원소의 집합에서 주어진 항목에 따라 크기 순서대로 늘어놓은 것.
항목들을 체계적으로 정리하는 과정으로 데이터의 순서를 결정하는 것.

• 오름차순 / 내림차순 으로 나열한다.
• 데이터를 저장하는 위치에 따라 내부정렬 / 외부정렬 로 구분한다.

내부정렬 : 데이터의 양이 적은 경우 주기억장치 내에 저장된 자료를 대상으로 정렬하는 방법
외부정렬 : 외부기억장치에 대부분의 데이터가 있고 일부만 주기억장치에 저장된 상태에서 정렬하는 방법 

• 효율적인 정렬 : 다른 알고리즘을 최적화하는데 중요한 역할을 한다.

이 알고리즘의 결과는 다음 두 가지를 반드시 만족해야함.

1) 출력은 비 내림차순이다. 
2) 출력은 입력을 재배열하여 만든 순열이다.

정렬대상

일반적으로 정렬시켜야 될 대상 : 레코드(Record), 필드(field)라는 보다 작은 단위로 구성되며 키필드로 레코드와 레코드를 구별

정렬방법 : 내부정렬

복잡성과 효율성으로 분류한다.

선택 정렬

Selection Sort
: 원소 교환 방식으로 정렬, 잘못된 위치에 들어가 있는 원소를 찾아 그것을 올바른 위치에 재배치해 정렬한다.

• 왼쪽부터 자기자리를 찾아간다.

1) 리스트 중 가장 작은 원소를 찾아 첫 번째 위치의 원소와 교환
2) 두 번째로 작은 원소를 찾아 두 번째 위치의 원소와 교환 이 과정 반복

복잡도(전체 수행 시간) : O(n^2)

버블 정렬

Bubble Sort
: 두 인접한 원소를 검사하여 정렬, 이웃한 두 개의 원소를 비교하여 순서가 서로 다르면 원소의 자리를 서로 바꾸고, 그렇지 않으면 그 위치에 그대로 둔다.

• 속도가 상당히 느리지만, 코드가 단순하기 때문에 자주 사용됨.
• 오른쪽부터 자기자리를 찾아간다.

1) 인접한 2개의 레코드를 비교하여 순서대로 되어 있지 않으면 서로 교환한다.
2) 이러한 비교와 교환 과정을 리스트의 왼쪽 끝에서 오른쪽 끝까지 반복하여 스캔한다. 

복잡도(전체 수행 시간) : O(n^2)

삽입 정렬

Insertion Sort
: 원소 중에서 가장 첫 번째 값을 정렬된 원소로 가정하고 그 다음 원소부터 정렬된 원소를 기준으로 적합한 위치에 삽입한다.
복잡도(전체 수행 시간) : O(n^2)

퀵 정렬

Quick Sort
: 분할 정복 정렬 방법의 하나, 평균적으로 가장 빠른 정렬 방법.

• 전체 데이터를 한번에 정렬하는 것이 아니라 데이터를 나누어 2개의 작은 데이터 집합을 정렬하는 것이 더 빠르다는 것에 출발함.
• 오름차순 정렬 : 주어진 파일의 첫 번쨰 데이터를 중심으로 정렬
• 프로그램에서 재귀호출을 이용하기 때문에 스택이 필요함.
• 리스트를 2개의 부분리스트로 비 균등 분할하고 각각의 부분리스트를 다시 퀵 정렬한다.
• 나누는 한 원소 중심 값을 피벗(pivot)이라고 한다.
  복잡도(전체 수행 시간) 최적 : O(n logn)
  복잡도(전체 수행 시간) 최악 : O(n^2)

합병 정렬

merge Sort
: 원소 집합을 비슷한 크기로 반복해서 나누고 나눈 원소들의 집합의 크기가 1이 되었을 때 정렬된 두 원소 집합을 병합하여 크기가 2인 집합들을 생성하고, 다시 이 집합들에 대해 병합 과정을 반복 시행해 한 개의 집합을 만들어 내는 방법이다.

2-way 병합 과정 : 두 개의 서로 다른 정렬된 집합을 합하여 하나의 정렬된 집합으로 만드는 병합 방식
n-way 병합 과정 : n 개의 서로 다른 정렬된 집합을 하나의 정렬된 집합으로 만드는 병합 방식

• 분할 정복 사용

분할 : 배열을 같은 크기의 2개의 부분 배열로 분할
정복 : 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 재귀호출을 이용해 다시 분할 정복 기법을 적용한다. (최대한 작은 사이즈로 만듬)
결합 : 정렬된 부분 배열을 하나의 배열에 통합한다.

복잡도(전체 수행 시간) : O(n logn)

힙 정렬

Heap Sort
: 원소 정리 시 동시에 처리하지 않고 모든 원소들 중에서 가장 큰 또는 작은 원소를 찾아서 출력하고, 나머지 원소들 중 가장 큰 또는 작은 원소를 찾아 출력하는 과정을 반복 시행하여 정렬하는 방법

• 최대 힙 트리 / 최소 힙 트리를 구성해 정렬하는 방법

내림차순 : 최대 힙 구성
오름차순 : 최소 힙 구성

수행시간 : O(log2n) 이진 트리를 최대 힙으로 만들기 위해 최대 힙으로 재구성하는 과정이 트리의 깊이만큼 이루어짐
복잡도 : O(n logn) 구성된 최대 힙으로 힙 정렬을 수행하는데 걸리는 전체시간(힙 구성 시간 + n개의 데이터 삭제 및 재구성 시간)

쉘 정렬

Shell Sort
: 삽입 정렬을 확장한 개념으로 원소 전체를 삽입 정렬하기 전에 원소들을 몇 개의 부분리스트로 나누어 삽입 정렬을 한 뒤 전체 원소에 대해 삽입 정렬 수행.
복잡도 : O(n log2n)

정렬방법 : 외부정렬

• 레코드 판독 및 기록에 걸리는 시간이 중요하다.
• 런(run) : 하나의 화일을 여러 개로 분할하여 내부 정렬 기법으로 정렬시킨 부분 파일(subfile)
  런들을 합병하여 원하는 하나의 정렬된 파일로 만듬.
• 보조기억장치에 접근해야함으로 내부정렬보다 느리다.
• 1) 정렬 단계(external sorting)
  정렬한 파일의 레코드들을 지정된 길이의 부분 파일로 분할해서 정렬하여 런을 만들어 입력 파일로 분배하는 단계.
  런 생성 방법 : 내부 정렬, 대체 선택, 자연 선택
• 2) 합볍 단계(merge phase)
  정렬된 런들을 합병해 보다 큰 런으로 만들고, 이것들을 다시 입력 파일로 재분배하여 합병하는 방식. 모든 레코드들이 하나의 런에 포함되도록 만드는 단계,

균형 합병 정렬

Balanced merge Sort
: n개의 테이프 장치에 대해 각 테이프에 똑같은 크기의 레코드들을 작은 블록으로 나누어 내부 방법을 통해 정렬

• 최소 4개의 테이프가 있을 때 가능
• 2-way-merge sort 방법

계단식 합병 정렬

Cascade merge Sort
: 부분적으로 정렬된 부분 파일들을 한 개의 빈 테이프에 합병하여 정렬하는 방법을 반복 실행하여 정렬하는 방법

• 연속 합병 정렬

교대 합병 정렬

Oscillating merge Sort
: 테이프의 읽기, 쓰기, 기능이 역방향과 순방향 모두 가능한 테이프 장치의 기능을 이용해 정렬하는 방법

다단계 합병 정렬

Polyphase merge Sort
: 분산되어 기록된 레코드의 수를 피보나치 수열을 이용해 정렬하는 방식.

• 최소 8개의 테이프가 있을 때 가능
• k-way-merge sort 방법

유클리드 알고리즘

: 유클리드 호제법
두 양의 정수 x,y가 갖는 공약수 중에서 최댓값인 최대 공약수를 찾는 알고리즘

r = x mod y (0 <= r <= y)가 성립할 때 최대공약수를 GCD(x,y)라고 했을 때 다음식이 성립함
GCD(x,y) = GCD9y,r)