관계
: 객체들 간의 연관성을 표현한다.
- 다른 두 집합에 속하는 서로 다른 두 원소의 관련사항
→순서쌍 집합으로 표현함- 관계를 표현하는 대표적인 방법 : 집합
ex) a와 b가 관계가 있는 경우 : aRb => (a,b) ∈ R : 이항 관계
이항 관계
Binary relation
- R : 두 집합의 곱집합
A X B의 부분집합
정의역(domain)
: 관계 R의 원소인 순서쌍에서 첫번쨰 원소의 집합.
dom(R) = {a|(a,b) ∈ R} ⊆ A
치역(range)
: 관계 R의 원소인 순서쌍에서 두번쨰 원소의 집합.
ran(R) = {b|(a,b) ∈ R} ⊆ B
공변역(Codomain)
: 관계 R의 원소인 순서쌍에서 두번쨰 원소가 포함되어 잇는 집합
codom(R) = {b|b ∈ B} ⊆ B
역관계
: 집합 A에서 집합 B로의 관계 R에 대해 역관계 R^-1은 집합 B에서 집합 A로의 관계를 의미한다.
R^-1 = {(b,a)|(a,b) ∈ R}
관계의 표현
1) 서술식 방법
집합 A = {1,2,3}에서 원소 a1,a2가 a1>=a2인 관계 R과 같이 표현2) 나열식 방법 : 서술식에 따라서 관계를 순서쌍들로 표현
R = {(1,3),(1,5),(3,5)}
- 관계는 일반적으로 순서쌍의 집합으로 표현하지만 다른 방법도 많다.
화살표 도표
arrow diagram
: 정의역에 해당하는 원소에서 시작해 순서쌍 뒤에 있는 공변역에 해당하는 원소로 향하는 화살표
- 집합 A에서 집합 B의 관계 R의 순서쌍 집합
(a,b) ∈ R (a ∈ A, b ∈ B)일 때 집합 A에 있는 원소 a에서 집합 B에 있는 원소 b로 화살표를 그려서 관계를 표현한다.
좌표 도표
coordinate diagram
: 관계 R에서 정의역의 집합을 x축으로 하고, 공변역 집합을 y축으로 순서쌍의 원소가 만나는 지점에 점을 찍어 표현.
- x축 : 관계 R의 정의역 원소 집합 A 원소 표시
- y축 : 관계 R의 공변역 원소 집합 B 원소 표시
관계 행렬
relation matrix
: 부울(boolean) 행렬을 이용하여 관계를 표현하는 또 다른 방법cf) 부울 행렬은 행렬 안에 있는 모든 원소들의 값이 0 또는 1인 행렬이다.
- 행의 값 : 관계 R의 정의역 원소 집합 A 원소 표시
- 열의 값 : 관계 R의 공변역 원소 집합 B 원소 표시
- 관계가 있다면 행렬의 각 요소의 값은 1 / 관계가 없으면 0 으로 표현.
방향 그래프
directed graph
: 정의역에 속하는 원소에서 시작하여 공변역에 속하는 원소로 향하는 화살표를 그려서 표현
- 정의역과 공변역이 같은 집합인 관계. 죽, 하나의 집합에 대한 관계일 때 사용함.
- 집합 A의 각 원소를 그래프의 정점(vertex)로 표시
(a,b) ∈ R일 경우 a에서 b로의 화살표가 있는 연결선 (edge)로 표현하는 것
=> 관계 R에 대한 방향 그래프 라고 한다.
순환(loop) 발생 가능 : 동일한 정점에서 시작하여 끝나는 화살표가 그려진 연결선
합성 관계
Composite relation
: 이미 주어진 두 관계 R1, R2로부터 새로운 관계 R2 • R1를 만들어 내는 것.
- 조건 : R1의 치역이 R2의 정의역이 되는 경우
- 화살표 도표, 관계 행렬로 표현한다.
항등관계를 이용한 합성 관계 : 원래의 관계와 동일
집합 A의 항등 관계 정의IA = {(a,a)|a ∈ A}
- 곱셈의 항등원(1), 덧셈의 항등원(0)이 연산결과에 영향을 주지 않듯이 항등 관계와 어떤 관계를 합성하든지 결과 값에는 변화가 없다.
IAR = RIA = R
합성 관계의 거듭제곱은 집합 A에 대한 관계 R에 대하여 n = 1,2,3...일 때의 거듭제곱이다.
- 관계의 거듭제곱은
추이 관계를 판별하는 가장 좋은 방법이다.- 원소의 개수가 n개인 집합에 대한 관계 R을 n번 합성한 결과가 원래 관계 R의 부분 집합이 되면 추이 관계라 할 수 있다.
관계의 성질
집합 A에 대한 관계 R은 포함된 순서쌍 원소들의 구성에 따른 특정한 성질에 따라 분류된다.
추이 관계
transtive relation
: 집합 A의 원소 a, b, c에 대해 관계 R이(a,b) ∈ R이고(b,c) ∈ R이면(a,c) ∈ R인 관계를 만족하는 관계 R을 추이 관계라고함.
반사 관계
reflexive relation
: 집합 A의 모든 원소 x에 대하여 xRx를 만족하는 이항 관계
- 방향 그래프 : 그래프의 모든 정점에서 자기 자신을 가리키는 화살표, 순환이 존재함.
- 관계 행렬 : 대각선에 해당되는 모든 값이 1임.
ex) 작거나 같다 / 크거나 같다 / 부분집합이다 = 자기자신이 포함된다.
비반사 관계
irreflexive relation
: 집합 A의 모든 원소가 반사 관계를 만족하지 않는 이항 관계
(a,a) !∈ R인 관계- 방향 그래프 : 모든 원소들에 대해 순환이 존재하지 않음.
- 관계 행렬 : 대각원소들의 값이 모두 0임.
ex) 작다 / 크다
반사 관계와 비반사 관계
- 반사 관계가 아니라고 비반사 관계라고 할 수 없으며 그 반대에도 그렇다.
- 반사 관계도 아니고 비반사 관계도 아닌 관계는 존재할 수 있지만 두 관계를 만족하는 관계는 존재하지 않는다.
대칭 관계
sysmmetric relation
: 집합 A의 임의의 두 원소 a,b에 대해aRb이면bRa를 만족하는 이항 관계
- 대칭 관계가 항상 성립하는 것은 아니다.
- 방향 그래프 : 정점 a → b 로 화살표가 나가면 정점 b → a 로가는 화살표가 반드시 있다.
- 관계 행렬 : 대각선을 중심으로 행렬의 값이 서로 대칭.
반대칭 관계
antisysmmetric relation
: 집합 A의 임의의 두 원소 a,b에 대해aRb이고bRa이면 a=b를 만족하는 이항 관계
1) 반대칭 관계 O 대칭 관계 : R이 같다.
2) 반대칭 관계 O 대칭 관계 x : R이 작거나 같다.
관계의 폐포
: 어떤 집합의 그 위에 관계에 대한 닫힘(closure), 그 집합의 원소와 관계가 있는 원소가 항상 그 집합에 속한다는 성질.
- 폐포(closure)
그 집합을 포함하면서 그 성질을 만족시키는 가장 작은 대상.
원래의 관계에 순서쌍 원소를 추가하여 특정 성질에 맞게 만든 것.
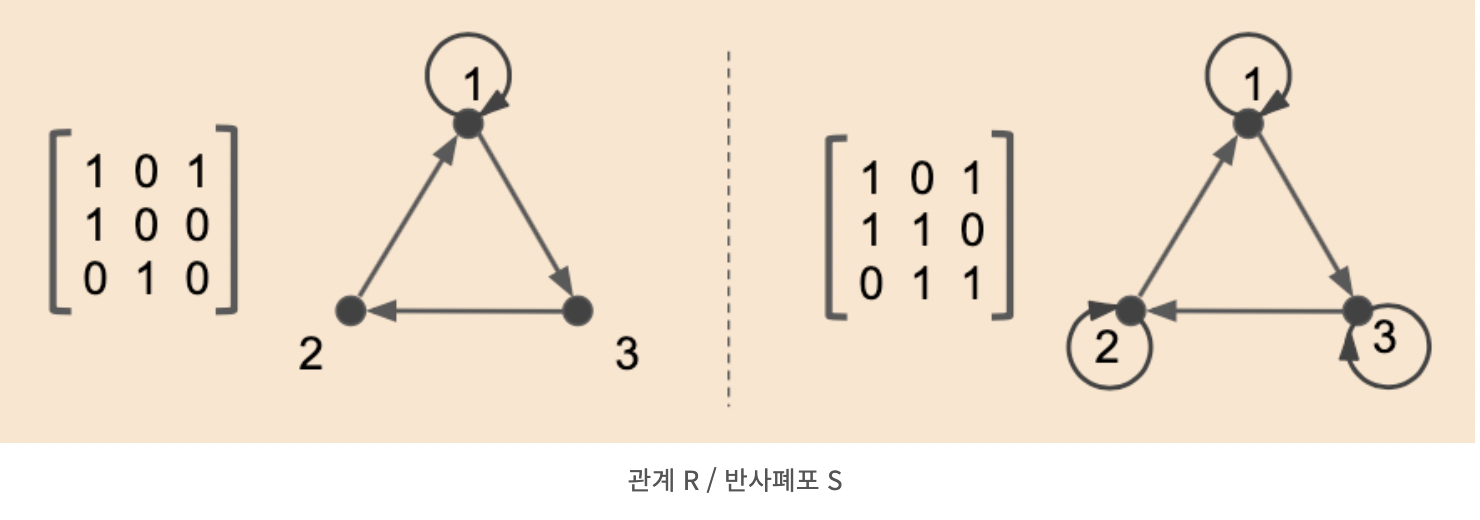
반사 폐포
reflexive closure
: 집합 A에 대해 관계 R1을 포함하면서 반사 관계를 갖는 관계 R2R2 = R1 ∪ {(a,a)|a ∈ A}
- 방향 그래프 : 그래프에 존재하는 모든 정점이 순환이 되도록함.
- 관계 행렬 : 대각선의 원소의 값을 모두 1로 만듦.
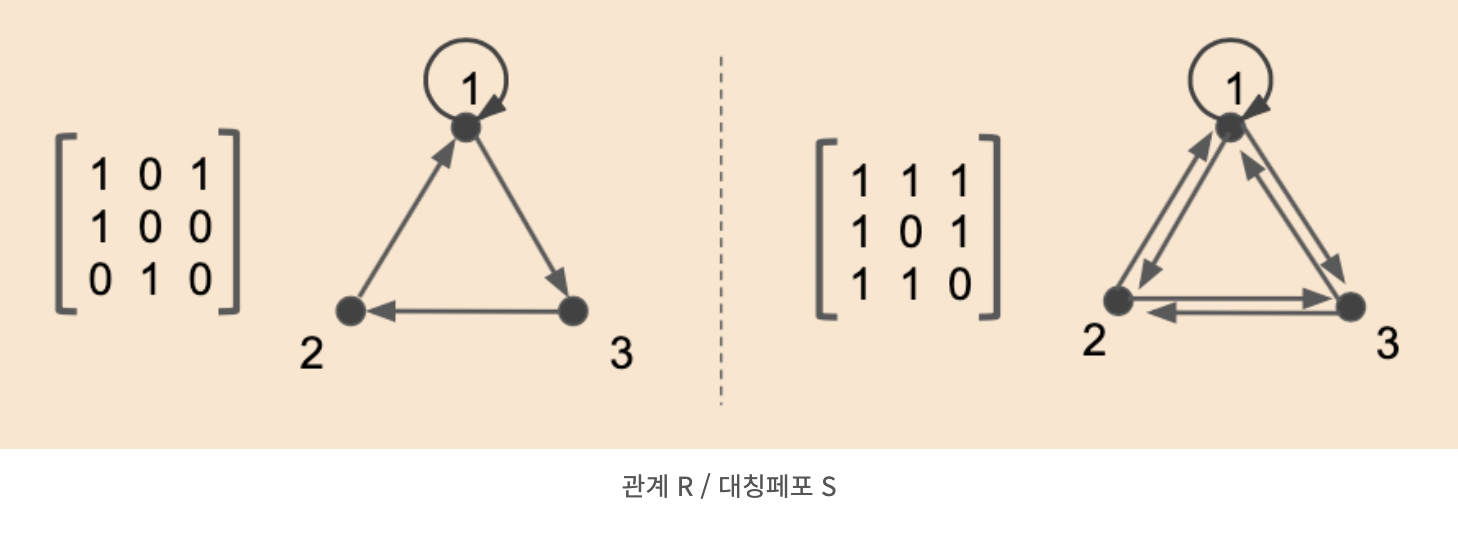
대칭 폐포
sysmmetric closure
: 집합 A에 대해 관계 R1을 포함하면서 대칭 관계를 갖는 관계 R2R2 = R1 ∪ {(b,a) ∈ A X A|(a,b) ∈ R} = R1 ∪ R1^-1
- 방향 그래프 : 한쪽으로만 향하는 단방향 화살표를 양방향으로 그림
- 관계 행렬 : 대각원소를 기준으로 마주하는 원소들이 같은 값을 갖도록 표기
추이 폐포
transtive closure
: 집합 A에 대해 관계 R1을 포함하면서 추이 관계를 갖는 R2R2 = R1 ∪ {(a,c) ∈ A X A|(a,b) ∈ R1 ∧ (b,c) ∈ R1}
- 방향 그래프 : 한쪽으로만 향하는 단방향 화살표를 양방향으로 그림
- 관계 행렬 : 대각원소를 기준으로 마주하는 원소들이 같은 값을 갖도록 표기