[머신러닝을 위한 기초수학] - 이산, 연속 확률분포

Binomial Distributions 이항분포

각각의 시행이 독립적이며, 성공 확률이 동일한 고정된 횟수의 시행에서 특정한 성공 횟수가 나올 확률을 나타내는 확률 분포

이항 분포는 n과 p 두 개의 매개변수를 가지며, n은 시행 횟수이고 p는 각 시행에서 성공할 확률
n번 시행에서 k번의 성공 확률은 이항 확률 공식으로 계산된다.

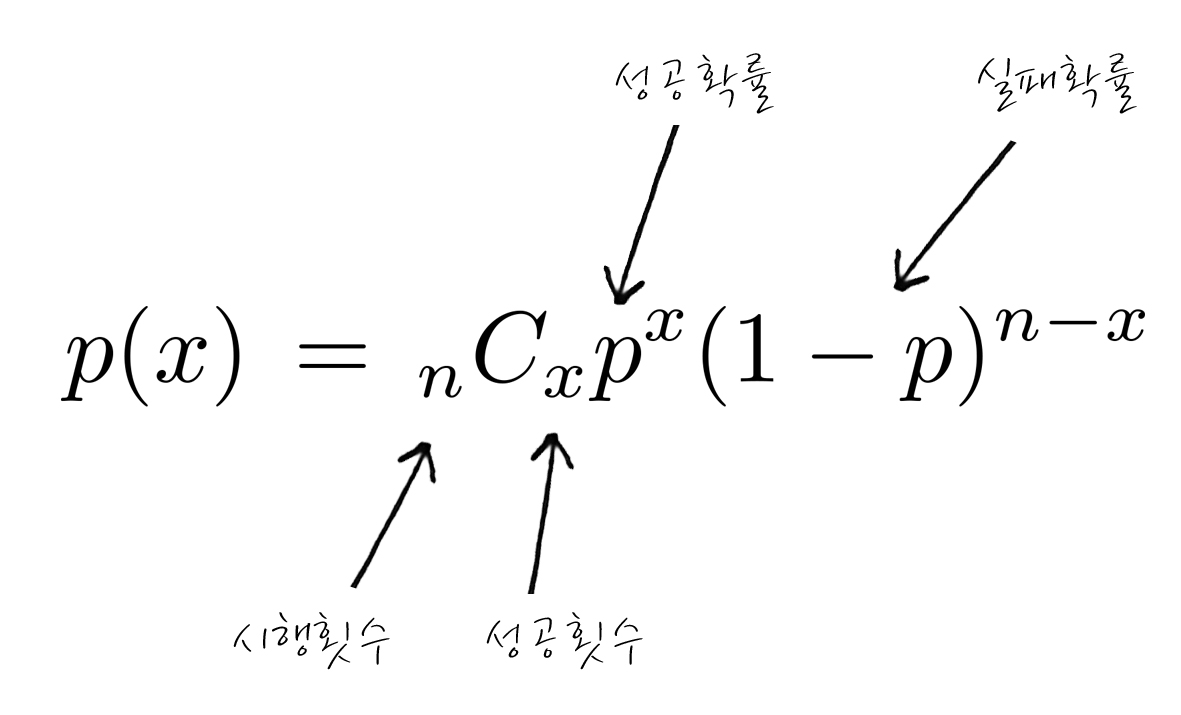
Normal Distributions 정규 분포

실제 세계 현상, 예를 들어 인구의 키나 표준화된 시험의 점수 등을 모델링하는 데 자주 사용되는 연속적인 확률 분포
그리고 종 모양의 특징적인 외양을 갖는 가우시안 분포 또는 벨 모양 곡선으로도 알려져 있다.

정규 분포는 평균 (μ)과 표준 편차 (σ) 두 개의 매개 변수를 가진다.
평균은 분포의 중심을 나타내며 표준 편차는 분포의 퍼짐 정도를 제어함!

정규 분포의 확률 밀도 함수 f(x) = (1 / (σ * sqrt(2π))) * exp(-((x - μ)^2) / (2σ^2))

여기서 x는 확률 변수의 값이고, σ는 표준 편차, μ는 평균, π는 수학 상수인 pi

정규 분포는 68-95-99.7 규칙과 같은 여러 가지 중요한 특성을 갖고 있다.
이 규칙은 대략 68%의 값이 평균에서 표준 편차의 범위 내에 있고, 대략 95%의 값이 평균에서 두 배의 표준 편차 범위 내에 있으며, 대략 99.7%의 값이 평균에서 세 배의 표준 편차 범위 내에 있다는 것을 나타냄!