[머신러닝을 위한 기초수학] - 베이즈 정리(Bayes’ Theorem)

베이즈 정리 : 새로운 정보나 증거를 기반으로 사건에 대한 믿음이나 확률을 업데이트하는 확률 이론의 기본 개념

P(A|B) = P(B|A) ⋅ P(A) / P(B)

P(A|B)는 사건 B가 발생한 경우 사건 A가 발생할 조건부 확률
P(B|A)는 사건 A가 발생한 경우 사건 B가 발생할 조건부 확률
P(A)는 사건 A가 발생할 사전 확률 또는 새로운 증거를 고려하기 전에 발생 확률
P(B)는 사건 A와 상관없이 발생할 확률 또는 새로운 증거의 발생 확률

간단히 말해서,
베이즈 정리는 새로운 증거 또는 관측 (P(B|A))와 사건과 관련없이 관측이 발생할 확률 (P(B))을 고려하여 사건 A에 대한 이전 믿음 (P(A))을 업데이트하는 방법을 제공한다.
이 업데이트된 믿음은 사후 확률 P(A|B)로 나타낼 수 있다.

즉, 구하기 어려운 확률을 쉬운 확률로 치환해서 구할 수 있다.

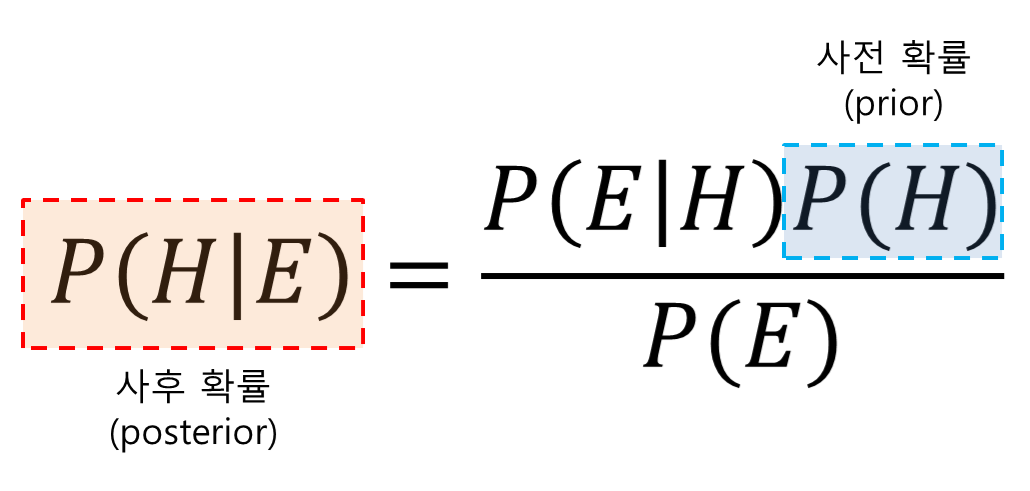
* 예상 시험문제

1. 어떤 병에 걸릴 확률이 1%이고, 그 병을 진단하는 검사의 정확도는 90%입니다.
   이 검사에서 양성 판정을 받았을 때, 실제로 병에 걸린 확률은 얼마인가요?
   (P(병에 걸린 경우) = P(A),
   P(양성 판정을 받은 경우) = P(B),
   P(양성 판정을 받은 경우 병에 걸린 경우) = P(B|A))

P(병에 걸린 경우 | 양성 판정을 받은 경우) = P(B|A) * P(A) / P(B)
= 0.9 * 0.01 / ((0.9 * 0.01) + (0.1 * 0.99))
= 0.0833 (약 8.33%)
따라서, 이 검사에서 양성 판정을 받았을 때 실제로 병에 걸린 경우는 약 8.33%일 것이다.

2. 주식 시장에서 특정 회사의 주가가 내일 상승할 확률이 60%입니다.
   그런데 믿을 만한 소식통으로부터 그 회사의 새로운 제품이 출시될 것이라는 정보를 들었습니다.
   이 정보를 고려할 때, 내일 그 회사의 주가가 상승할 확률은 얼마인가요?
   (P(주가 상승) = P(A),
   P(새 제품 출시) = P(B),
   P(새 제품 출시일 때 주가 상승) = P(A|B))

P(주가 상승 | 새 제품 출시) = P(A|B) = (P(B|A) * P(A)) / P(B)
= (0.6 * x) / ((0.6 * x) + (0.4 * (1-x)))
= 0.75 (약 75%)
따라서, 새 제품 출시라는 정보를 고려하면 내일 그 회사의 주가가 상승할 확률은 약 75%일 것이다.

베이즈 이론(Bayes’ Theorem)

P(Ct|D)는 주어진 증거 D에 대해 가설 Ct가 참일 확률
p(D|Ct)는 가설 Ct가 참일 때 증거 D가 관측될 확률
P(Ct)는 어떠한 증거도 관측하기 전 가설 Ct가 참일 확률
P(D)는 가설 Ct가 참이든 거짓이든 증거 D가 관측될 확률

간단히 말하면, 베이즈 정리는 주어진 증거에 대해 가설이 참일 확률이,
증거가 주어졌을 때 그 가설이 옳을 가능성과 해당 가설이 사전에 얼마나 참일 가능성이 있는지를 고려해 계산됨을 나타낸다.

* 예상 시험문제

당신은 어떤 병에 걸린 환자를 진료하고 있습니다.
이 병에 걸린 사람 중 95%는 양성 판정을 받고, 건강한 사람 중 2%는 양성 판정을 받습니다.
당신의 환자가 양성 판정을 받았을 때, 그 사람이 실제로 병에 걸렸을 확률은 얼마인가요?

가설 Ct: 환자가 병에 걸렸다
증거 D: 양성 판정을 받음

P(Ct|D) = p(D|Ct) x P(Ct) / P(D)

p(D|Ct) = 0.95 (병에 걸린 환자 중 양성 판정을 받을 확률)
P(Ct) = 0.01 (전체 환자 중 병에 걸릴 확률)
P(D) = 0.01 x 0.95 + 0.99 x 0.02 = 0.0293 (양성 판정을 받을 확률)
따라서,

P(Ct|D) = 0.95 x 0.01 / 0.0293 = 0.325

즉, 환자가 양성 판정을 받았을 때 그 사람이 실제로 병에 걸린 확률은 32.5%이다.
이 결과는 처음부터 병에 걸릴 확률이 매우 낮았기 때문에 양성 판정을 받았다 해서 반드시 실제로 병에 걸렸다고 단정할 수는 없음을 보여준다.