
확률변수(Random Variables) => Funcion 함수라 생각
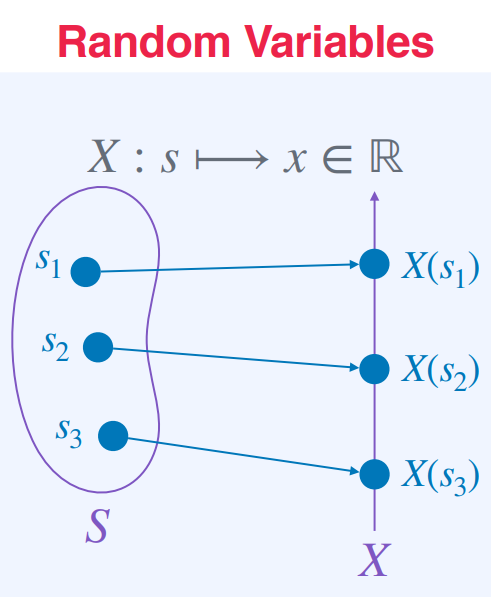
랜덤 변수 X는 표본 공간에서 각 결과 s에 대해 실수 x를 할당하는 함수이다.
즉, 각 가능한 결과 s에 대해 X(s)는 실수!
X가 취할 수 있는 모든 가능한 값의 집합을 X의 범위(Range)라고하며, Range(X)로 나타낸다.
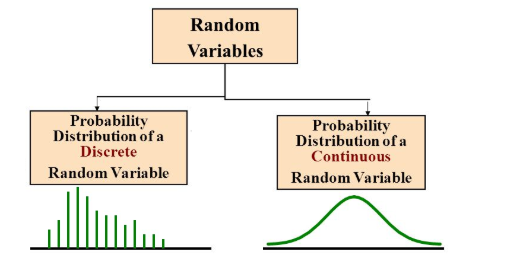
랜덤 변수는 이산적(discrete) 또는 연속적(continuous)일 수 있다.
이산적인 랜덤 변수는 계산 가능한 갯수의 값만 취할 수 있다.
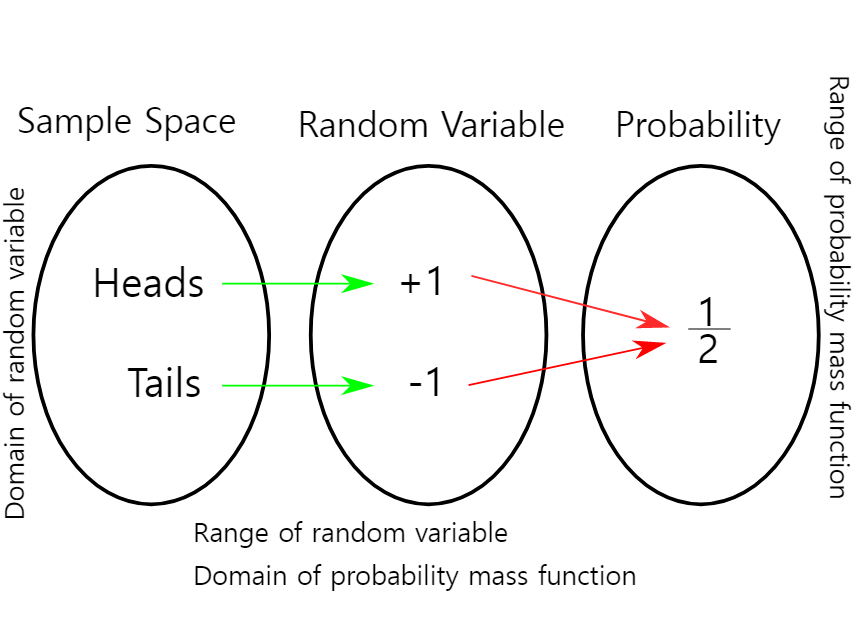
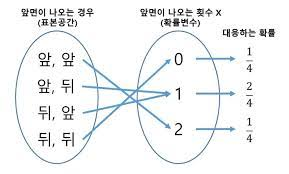
예를 들어, 동전을 3번 던져서 얻은 앞면의 수는 0, 1, 2 또는 3 값만 취할 수 있으므로 이산적인 랜덤 변수이다.
연속적인 랜덤 변수는 주어진 실수 범위에서 어떤 값이든 취할 수 있습니다.
예를 들어, 사람의 키는 0에서 무한대까지의 어떤 값이든 취할 수 있으므로 연속적인 랜덤 변수이다.
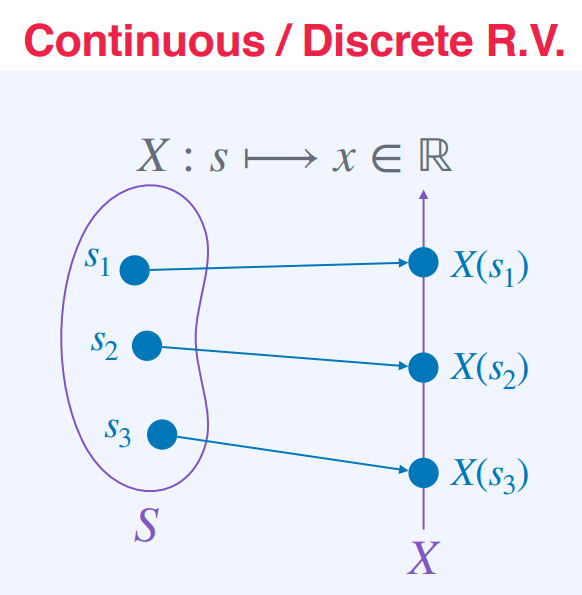
Continuous / Discrete R.V.
이산형 랜덤 변수(discrete random variable)
이산형 랜덤 변수(discrete random variable)는 값이 이산적인 랜덤 변수를 말한다.
이산적인 랜덤 변수는 값이 셀 수 있으며, 각 값에 대한 확률이 할당된다.
예를 들어, 동전을 던져서 앞면이 나오는 횟수를 나타내는 랜덤 변수는 0, 1, 2와 같은 이산적인 값을 가질 수 있다.
연속형 랜덤 변수(continuous random variable)는 값이 연속적인 랜덤 변수를 말한다.
연속적인 랜덤 변수는 범위 내에서 어떤 값이든 취할 수 있으며, 각 값에 대한 확률은 0이다.
예를 들어, 사람의 키를 나타내는 랜덤 변수는 어떤 높이든 취할 수 있으며, 특정 높이에 대한 확률은 0이다.
기댓값(Expected value)
시행을 할때 기대하는 확률변수의 값
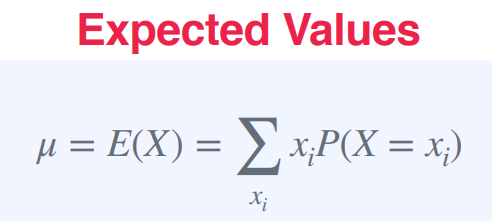
랜덤 변수 X가 가질 수 있는 값들의 가중 평균으로,
각 값 xi가 발생할 확률 P(X = xi)와 해당 값 xi의 가중치를 곱하여 모든 가능한 값들에 대한 가중 평균을 계산한 것
E(X) = μ = ∑ xi * P(X = xi)예를 들어, 동전을 던져서 앞면이 나오는 횟수를 나타내는 이산형 랜덤 변수 X를 생각해보자!
이 경우, X는 0, 1, 2의 값을 가질 수 있으며, 각 값에 대한 확률은 각각 1/2, 1/4, 1/4입니다. 이때, X의 기댓값은 다음과 같이 계산됩니다.
E(X) = μ = (0 1/2) + (1 1/4) + (2 * 1/4) = 1
따라서, 이 랜덤 변수 X의 기댓값은 1입니다.

확률변수의 기댓값(Expectations of a Function)
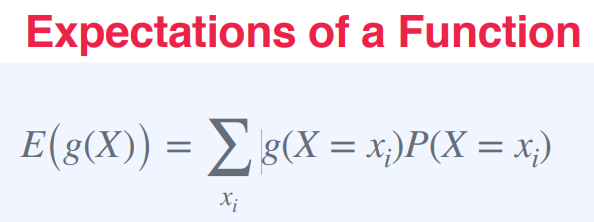
함수의 기댓값(Expected value of a function)은
랜덤 변수 X에 함수 g를 적용한 결과에 대한 기댓값으로, 각 값 xi가 발생할 확률 P(X = xi)와 함수 g(X)의 값을 곱하여 모든 가능한 값들에 대한 가중 평균을 계산한 것!
μ(뮤) = E(g(X)) = ∑ gi * P(X = xi)
*예상 시험문제
-
물리 시험에서 어떤 문제가 출제되었습니다.
이 문제는 점수 X를 랜덤 변수로 가지며, 이 변수의 확률 질량 함수가 다음과 같다고 가정합니다.P(X = 60) = 0.2
P(X = 70) = 0.3
P(X = 80) = 0.51) 이 랜덤 변수 X의 기댓값을 구하세요.
2) 이 랜덤 변수 X의 분산을 구하세요.
3) 만약 이 랜덤 변수 X의 값을 10점 추가했을 경우, 이 랜덤 변수의 새로운 기댓값을 구하세요.
E(X) = μ = (60 * 0.2) + (70 * 0.3) + (80 * 0.5) = 73
따라서, 이 랜덤 변수 X의 기댓값은 73이다.
이 랜덤 변수 X의 분산은 다음과 같이 계산할 수 있습니다.
Var(X) = E(X^2) - [E(X)]^2
E(X^2) = (60^2 * 0.2) + (70^2 * 0.3) + (80^2 * 0.5) = 6760
[E(X)]^2 = 73^2 = 5329
Var(X) = 6760 - 5329 = 1431
따라서, 이 랜덤 변수 X의 분산은 1431이다.
이 랜덤 변수 X의 값을 10점 추가했을 경우, 새로운 랜덤 변수 X'는 X + 10이 된다.
이 랜덤 변수 X'의 기댓값은 E(X') = E(X + 10) = E(X) + 10
따라서, 이 랜덤 변수 X'의 기댓값은 83이다.- 학생들의 수학 시험 점수를 나타내는 확률변수 X의 분포가 다음과 같이 주어졌다고 하자.
또한, 이 학급의 평균 점수를 g(X)로 정의하면, g(X) = (1/4) * (X + 10)이다.
이때, 확률변수 g(X)의 기댓값을 구하시오.

확률변수 g(X)의 기댓값은 각 점수값에 대한 g(X)의 값과 그 점수값이 나올 확률의 곱을 모두 더한 값이다.
E(g(X)) = (1/4) * [(60 + 10) × 0.2 + (70 + 10) × 0.3 + (80 + 10) × 0.4 + (90 + 10) × 0.1]
= (1/4) * [14 + 24 + 34 + 10]
= 20
따라서, 확률변수 g(X)의 기댓값은 20이다.