
벡터 : 크기(또는 길이)와 방향 모두를 가지는 수학적 객체
실수의 문맥에서, ℝ^n 벡터는n개의 실수 모음으로 나타낸다.
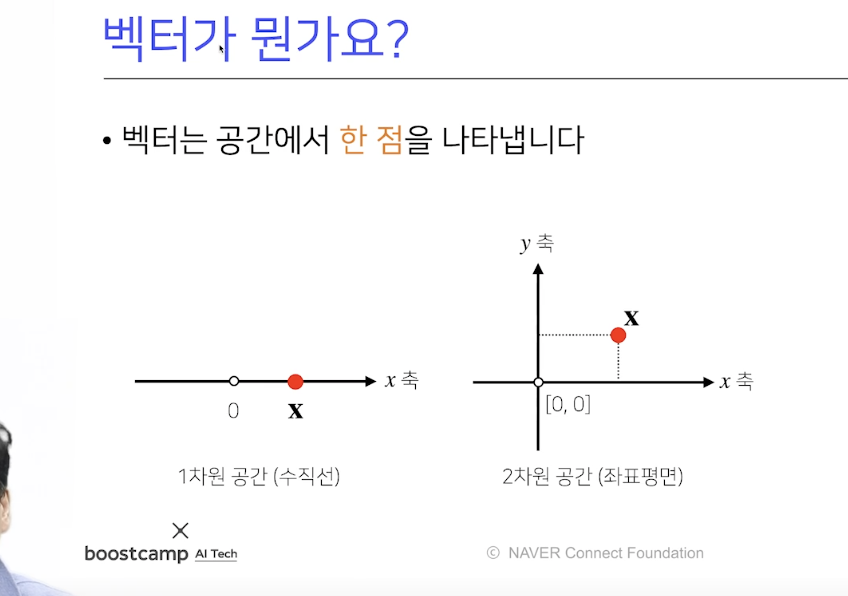
u = [u1, u2, ..., un]여기서 각각의 ui는 실수이며, 벡터 u는 n차원 공간에서의 한 점을 나타낸다.
예를 들어, n = 2인 경우, u는 평면상의 한 점을 나타내고, n = 3인 경우, u는 3차원 공간상의 한 점을 나타낸다.
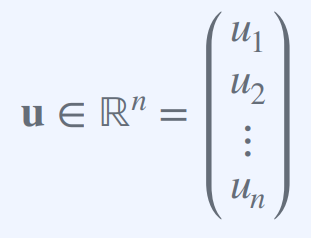
벡터의 전치(Transposes of Vectors) : 행 벡터를 열 벡터로, 또는 그 반대로 바꾸는 방법
-
행 벡터 v = [v1, v2, ..., vn]가 주어졌을 때, 그 전치는 v^T로 나타내며 다음과 같이 정의된다.
v^T = [v1; v2; ...; vn]
각각의 vi는 스칼라이고, 세미콜론 (;)은 각 요소를 별개의 행으로 구분한다.
따라서 v^T는 열 벡터(column)가 된다. -
열 벡터 u = [u1; u2; ...; um]가 주어졌을 때, 그 전치는 u^T로 나타내며 다음과 같이 정의된다.
u^T = [u1, u2, ..., um]
각각의 ui는 스칼라이고, 쉼표(,)는 각 요소를 별개의 열로 구분한다.
따라서 u^T는 행 벡터(row)가 된다.참고)
스칼라는 수학에서 크기만을 가지는 양을 나타내는 용어
즉, 크기를 가지고 방향이 없는 양을 스칼라라고 한다.스칼라는 벡터와 대비되는 개념!
벡터는 크기와 방향을 가지는 양으로, 여러 개의 스칼라를 모아 놓은 것예를 들어, 5kg과 같은 질량은 스칼라이며, 크기만을 가지고 방향이 없다.
반면에, 5m/s의 속도는 크기와 방향을 모두 가지므로 벡터이다.
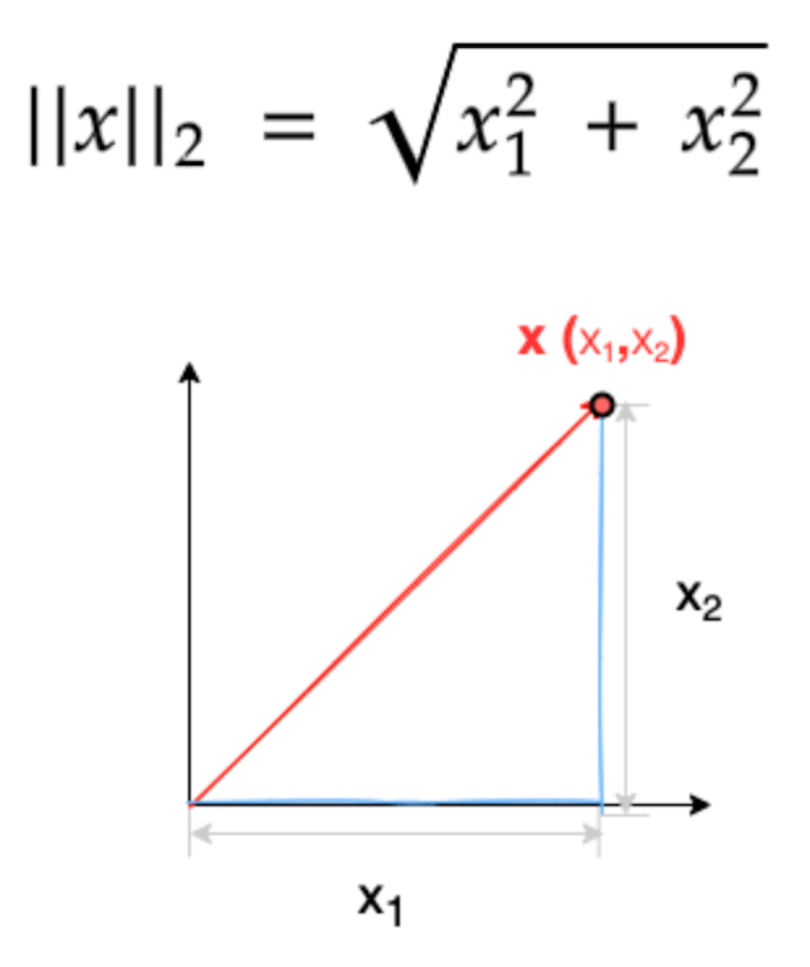
Vector Norms 노름 : 벡터의 크기를 나타내는 개념 ∥u∥
즉, 각 성분의 제곱을 더한 후, 그 값의 제곱근을 구하면 벡터 u의 크기가 된다.
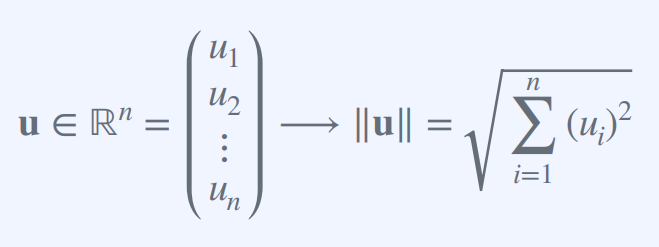
벡터의 스칼라곱(Scalar Multiplications of Vectors)
벡터의 스칼라 곱은 벡터의 각 성분에 스칼라 값을 곱하는 것을 의미한다.
즉, 만약 벡터 v가 다음과 같다면
v = [v1, v2, ..., vn]그리고 k가 스칼라 값이라면, v에 k를 곱한 결과는 다음과 같다.
k * v = [k * v1, k * v2, ..., k * vn]여기서 k * v는 각 성분에 k를 곱한 벡터를 나타낸다.
이러한 스칼라 곱은 벡터를 확대 또는 축소시키는 효과가 있다.
예를 들어, k가 2보다 큰 양수인 경우, 벡터 v를 확대시키고, k가 1보다 작은 경우, 벡터 v를 축소시킨다.
또한, k가 음수인 경우, 벡터의 방향이 반대가 된다.
이러한 성질들은 벡터의 선형 변환(linear transformation)에서 유용하게 사용된다!
벡터의 단위화(unitization)
벡터의 단위화(unitization)는 벡터의 크기를 1로 만드는 것을 의미
즉, 벡터 u가 있다면, 단위 벡터(unit vector) û 는 다음과 같이 정의된다.
û = (u)/ ∥u∥
여기서 분자(u)는 n차원 벡터, 분모(∥u∥)는 스칼라 값이다. 여기서 ∥u∥는 벡터 u의 크기(norm)를 나타내며, û는 크기가 1인 벡터이다.
따라서, 만약 벡터 u의 크기가 1이라면, 즉 ∥u∥ = 1인 경우에는 û = u가 성립!
이러한 단위 벡터는 방향을 나타내는 데에 유용하게 사용된다.
-
∥u∥ = 1 -> u is an unit vector (단위원 안에서 가리키는 모든 벡터)
-
û는 윗첨자로 표기되어 있으며, 이는 해당 벡터가 단위 벡터임을 나타냄. (hat(^)이라 읽음)

참고)
만약 두 벡터 u와 v의 크기가 같고, 같은 차원을 가지고 있다면,
벡터의 덧셈(또는 뺄셈)은 각 성분별로 덧셈(또는 뺄셈)을 수행하여 새로운 벡터 w를 생성할 수 있다.
u + v = [u1 + v1, u2 + v2, ..., un + vn] >> 벡터의 덧셈
u - v = [u1 - v1, u2 - v2, ..., un - vn] >> 벡터의 뺄셈
벡터의 선형 조합(Linear Combinations of Vectors)
벡터의 선형 조합은 두 개 이상의 벡터의 스칼라 배수의 합으로 나타낼 수 있는 벡터를 말한다.
즉, 실수 α와 β가 있고, u와 v가 ℝn에서의 벡터이면,
계수로 α와 β를 가지는 u와 v의 선형 조합은 벡터 αu + βv이다.
예를 들어, u = [1, 2, 3]이고 v = [-1, 0, 1]이며, α = 2이고 β = -1이라고 가정해보자!
그러면, 계수가 α와 β인 u와 v의 선형 조합은 다음과 같다.
αu + βv = 2[1, 2, 3] + (-1)[-1, 0, 1] = [2, 4, 6] + [1, 0, -1] = [3, 4, 5]따라서, 계수가 α = 2이고 β = -1인 u와 v의 선형 조합은 벡터 [3, 4, 5]이다.
내적(dot product) : 두 벡터 사이의 스칼라 값을 반환하는 수학적 연산
내적은 스칼라 곱(scalar product) 또는 내적 곱(inner product)이라고도 한다.
두 벡터 A와 B 사이의 내적(dot product)은 다음과 같이 정의된다.
A·B = |A||B|cos(θ)여기서 |A|와 |B|는 각각 벡터 A와 B의 크기이며, θ는 두 벡터 사이의 각도이다.
ex. 내적 예시
두 벡터 u = [1, 2, -3]와 v = [4, -5, 6]의 내적(dot product)을 계산하는 문제벡터의 크기는 피타고라스의 정리를 이용하여 계산한다.
u와 v의 크기는 다음과 같다.
∥u∥ = √(1^2 + 2^2 + (-3)^2) = √14
∥v∥ = √(4^2 + (-5)^2 + 6^2) = √77다음으로, 두 벡터의 내적(dot product)을 계산한.
내적은 각 벡터의 각 구성 요소를 곱한 후 더한 값을 구하는 것!
따라서, 벡터 u와 v의 내적은 다음과 같다.
u · v = (1 × 4) + (2 × -5) + (-3 × 6)
= 4 - 10 - 18
= -24마지막으로, 두 벡터 사이의 각도 θ를 계산한다.
cos(θ) = (u · v) / (∥u∥ ⋅ ∥v∥)이므로,
cos(θ) = -24 (√14 ⋅ √77) = -0.915위의 결과를 역삼각함수 arccos를 이용하여 각도로 변환한다.
θ = arccos(-0.915) ≈ 163.6°
따라서, 두 벡터 u와 v의 내적(dot product)은 -24이며, 두 벡터 사이의 각도는 약 163.6°도이다.

