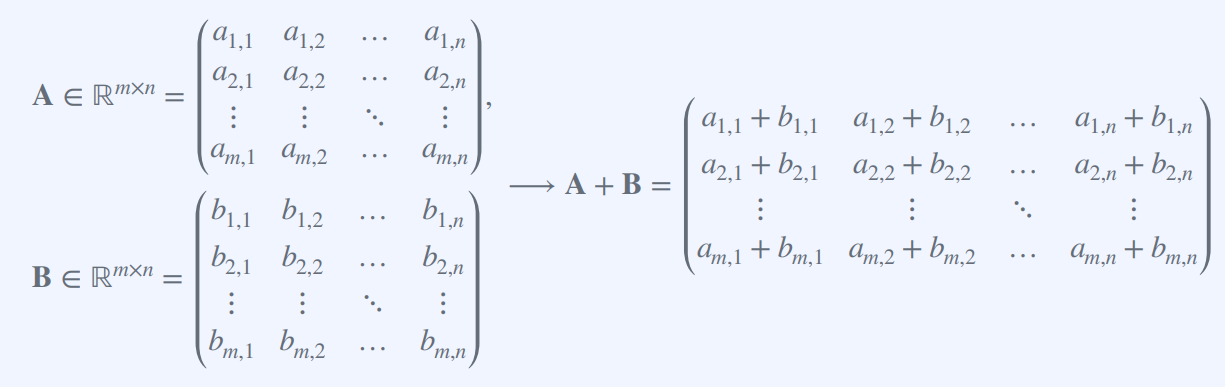행렬(Matrix) : 수학적인 객체로, 숫자들을 사각형 형태로 배열한 것이다.
각 숫자들은 해당 행렬의 원소(element)라고 부른다.
행렬은 선형 대수학과 컴퓨터 과학 분야에서 매우 중요한 역할을 한다.
특히, 컴퓨터 그래픽스나 기계 학습 분야에서 이미지나 데이터를 다루는 데에 행렬을 자주 사용한다.

행렬의 전치(Transposes of Matrices) : 해당 행렬의 행과 열을 서로 바꾸어 얻는 새로운 행렬을 의미
행렬 A의 전치는 A^T라고 표기되며, 매트릭스(Matrix)로 표현하면 다음과 같다.
만약 A가 크기가 m x n이라면, A^T는 크기가 n x m인 행렬이다.
A^T의 각 원소는 A의 원소와 같지만, 행과 열의 인덱스가 서로 바뀐 것을 의미한다.
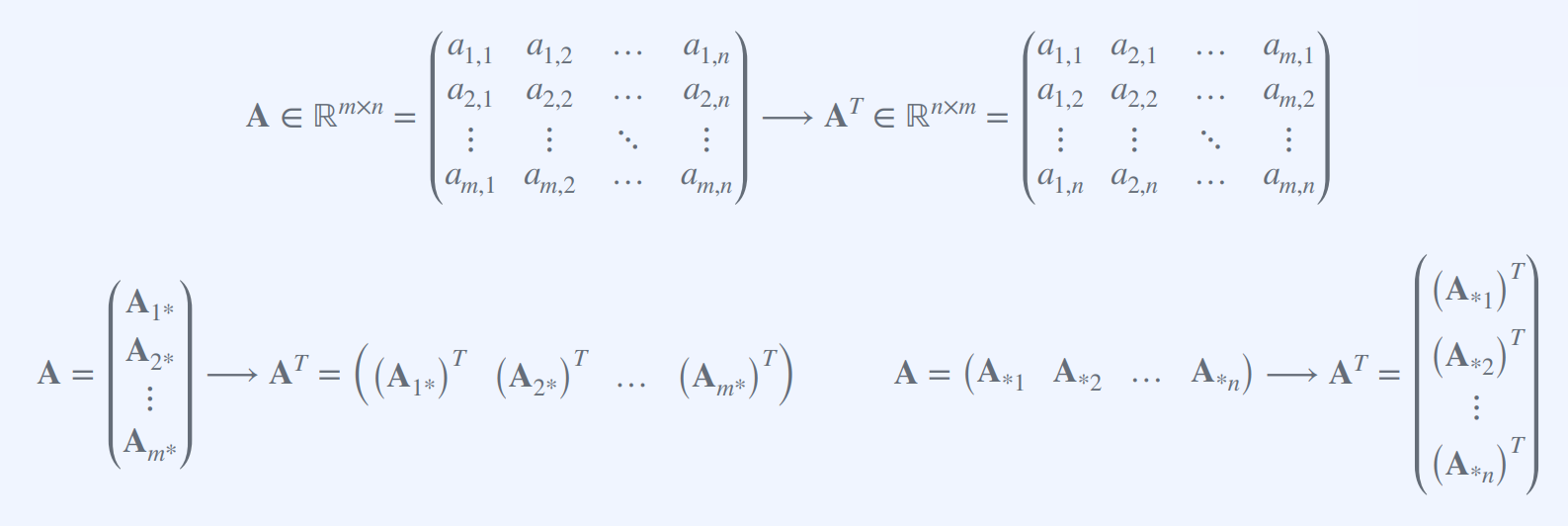
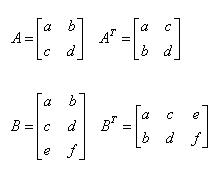
참고)
벡터와 마찬가지로 행렬과 스칼라(scalar)의 곱셈도 행렬의 모든 원소에 스칼라 값을 곱한 결과를 반환한다.

행렬 덧셈(matrix addition) : 두 행렬 A와 B의 덧셈은 A와 B가 같은 크기를 가지고 있을 때에만 가능하다. = 행과 열의 갯수가 동일해야한다.

[AB]ij : A의 i행과 B의 j열의 내적(dot product)
내적은 각 성분을 곱한 뒤 모두 더한 값이다.

행렬-벡터 곱셈에 대한 항등원(identity) : m차원 벡터 공간에서의 0벡터
만약 어떤 n x n 행렬 X에 대해 AX = A이면, X는 행렬 곱셈의 항등원(identity)이 된다.
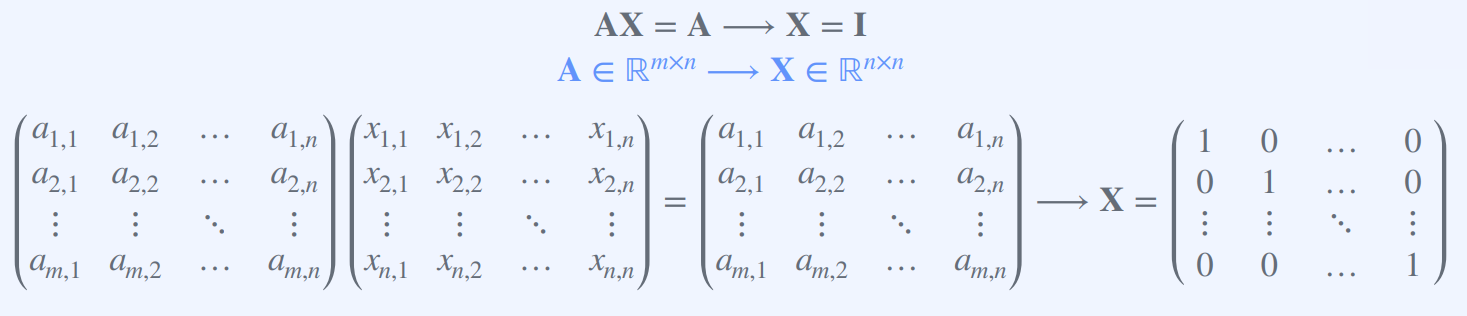
행렬-벡터 곱셈에 대한 역원(Inverses)
만약 어떤 n x n 행렬 X가 AX = I를 만족한다면, X는 A의 역행렬(inverse matrix)이 된다.
참고로 A의 역행렬을 A^-1으로 표기한다.
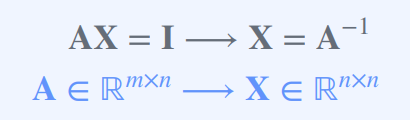

역행렬(Inverse Matrices)

-
행렬식(determinant)은 정방행렬(square matrix)에 대해서만 정의된다.
(*정방행렬 : 행과 열의 갯수가 같은 행렬)정방행렬 A의 행렬식은 det(A) 또는 |A|로 표기한다.
det(A) = |A| = ad - bc만약, ad - bc가 0이라면 역행렬이 존재하지 않는다.