
확률 변수 X의 분산의 정의 = 산포도(Variances)
σ^2 = Var(X) = E[(X-μ)^2] = E[X^2] - (E[X])^2X의 분산인 σ^2는 X와 X의 평균인 μ의 제곱 차이의 제곱의 기댓값과 같다.
여기서 E[X^2]는 X의 제곱의 기댓값이며, (E[X])^2는 X의 기댓값의 제곱
따라서 확률 변수 X의 분산(산포도)을 계산하려면
먼저 X의 제곱의 기댓값과 X의 기댓값을 계산한 후, 위의 식을 사용하여 분산을 구할 수 있다.

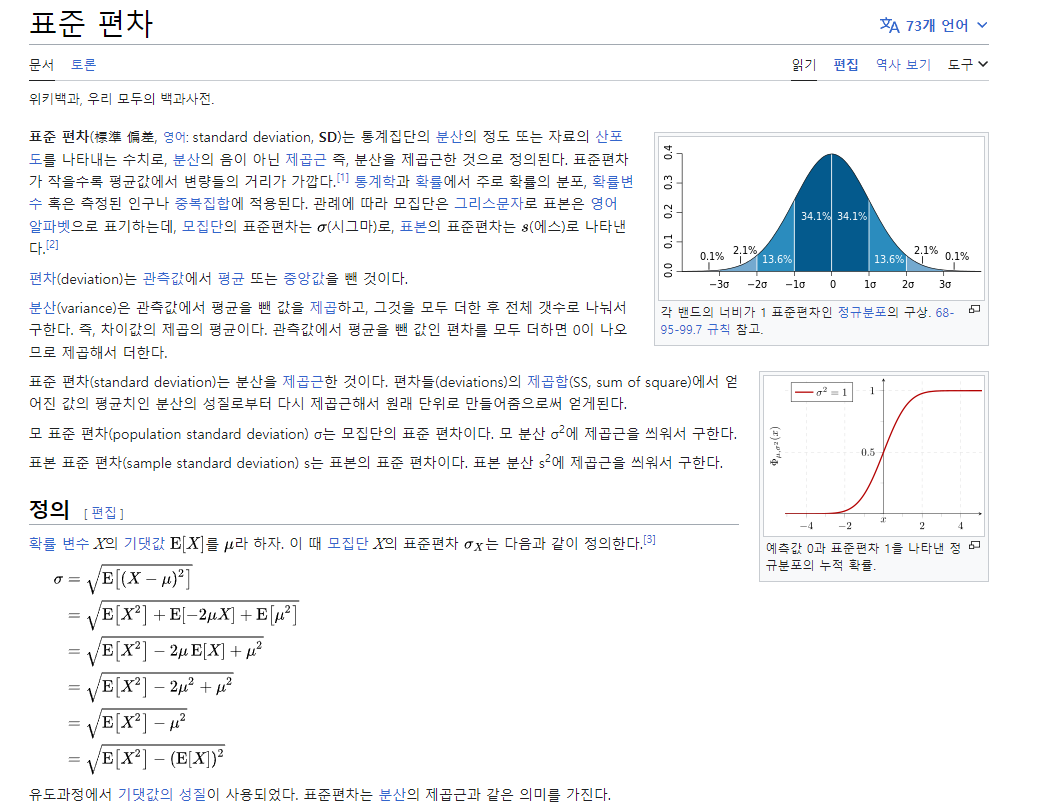
기호 σ는 확률 변수 X의 표준 편차를 나타낸다.
X의 분산을 양의 제곱근으로 나눈 값으로, Var(X)로 표기된다.
σ = sqrt(Var(X))여기서 sqrt()는 제곱근 함수를 나타냄
표준 편차는 X의 확률 분포의 분산이 얼마나 퍼져 있는지를 나타내는 측도.
이는 X의 값이 기댓값 또는 평균에서 얼마나 벗어나는지를 보여준다. 표준 편차가 크면 X의 값이 넓게 퍼져 있음을 나타내며, 작으면 값이 평균 근처에서 더 집중되어 있음을 나타낸다.
표준 편차는 X와 동일한 단위로 표현되며, 분산은 제곱 단위로 표현됩니다.
예를 들어, X가 학생들의 키를 미터로 나타내는 경우, X의 표준 편차도 미터 단위로 표현되며, 분산은 제곱 미터 단위로 표현된다.
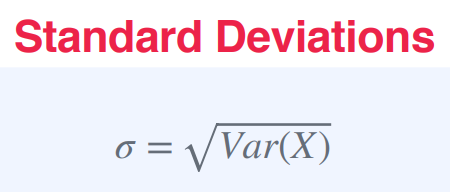
확률 질량 함수(PMF) / 확률 밀도 함수(PDF)
-
PMF는 이산형 확률 변수에 사용되며, 특정 결과가 발생할 확률을 제공.
PMF는 가능한 값인 x에 대해 f(x)로 표시됩니다.P(X = xi) = f(X = xi)
-
PDF는 연속형 확률 변수에 사용되며, 특정 지점의 확률 밀도를 제공
PDF도 f(x)로 표기됨.
하지만 확률 질량 함수 대신 확률 밀도 함수를 나타낸다.
따라서 연속형 확률 변수가 범위 [a,b] 내에 있을 확률은 그 범위에서 PDF의 적분으로 표현
P(a ≤ x ≤ b) = ∫ b a f(x)dx

이산확률변수의 평균, 분산, 표준편차의 성질 - 개념정리&기본문제
https://www.youtube.com/watch?v=eemADfHCuqM
