[머신러닝을 위한 기초수학] - 연립 선형방정식

선형 연립방정식(systems of linear equations)은 다음과 같은 형태의 방정식들의 집합이다.

a11x1 + a12x2 + ... + a1nxn = b1
a21x1 + a22x2 + ... + a2nxn = b2
...
am1x1 + am2x2 + ... + amnxn = bm

여기서 aij와 bi는 실수이다.
이 식을 행렬과 벡터의 곱으로 표현하면 Ax = b가 된다.
이때, A는 계수행렬(coefficient matrix)로서, aij를 원소로 갖는 m x n 크기의 행렬이다.
x와 b는 각각 n차원과 m차원의 열벡터(column vector)!

C(A) : A의 열공간(Column Space)

A의 모든 열 벡터의 선형조합으로 이루어진 집합

C(A) = {x | x = α1A1 + α2A2 + ... + αnA*n, ∀αi ∈ ℝ}

A1, A2, ..., A*n은 A의 각 열 벡터를 나타내며, α1, α2, ..., αn은 실수 상수
이는 A의 각 열 벡터들의 스칼라배와 합으로 나타낼 수 있는 모든 벡터의 집합을 나타냄

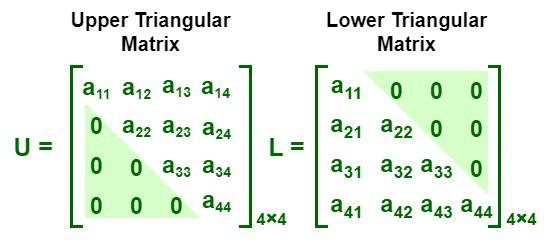
Triangular Matrices는 "상삼각행렬"과 "하삼각행렬"로 나뉜다.

1. 상삼각행렬 : 대각선 아래에 있는 모든 원소가 0인 행렬

2. 하삼각행렬 : 대각선 위에 있는 모든 원소가 0인 행렬
   
   

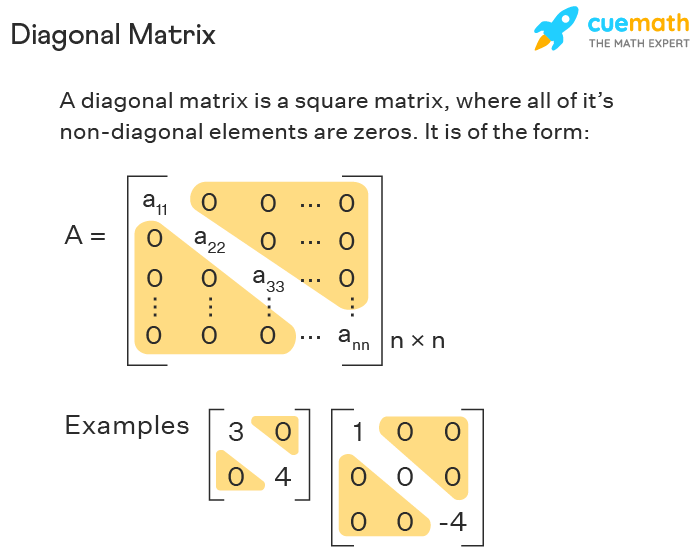
Diagonal Matrices는 대각선 위와 아래의 모든 원소가 0인 행렬
즉, 대각선 성분을 제외한 모든 원소가 0이다.