모델 기반 협업 필터링(Model Based Collaborative Filtering; MBCF)

Neighborbood-based CF(NBCF)의 한계

• MBCF는 다음과 같은 NBCF의 문제를 극복하고자 등장한 협업 필터링 방식이다.

Sparsity(희소성) 문제

• 데이터가 충분하지 않다면 유사도 계산이 부정확할 수밖에 없어 추천 성능이 떨어진다.
• Cold Start : 데이터가 부족하거나 없는 유저, 아이템의 경우 추천이 불가능하다.

Scalability(확장성) 문제

• 유저와 아이템이 늘어날 수록 선형적으로 유사도 계산량이 늘어난다.
• 즉, 유저와 아이템이 많아야 정확한 예측을 할 수 있지만, 반대로 계산량이 늘어나 시간이 오래 걸리는 Trade-Off 문제가 발생한다.

MBCF란?

• 유저-아이템 데이터 간 유사성을 단순히 비교하는 것에서 벗어나 데이터에 내재한 패턴을 이용해 추천하는 협업 필터링 기법이다.
• 즉, 주어진 데이터를 사용해 모델을 학습하는 Parametric Machine Learning을 사용한다.
• 데이터의 정보가 파라미터의 형태로 모델에 압축되어 있으며, 파라미터를 최적화를 통해 업데이트한다.

vs NBCF

• MBCF는 데이터에 숨겨진 유저-아이템 관계의 잠재적 특성/패턴을 찾는 협업 필터링 방식으로, 데이터를 바탕으로 유저-아이템 벡터를 계산된 형태로 저장하는 NBCF와 다르다.
• 현업에서는 NBCF보다 MBCF기반 Matrix Factorization(MF) 기법이 가장 많이 사용되며, 최근에는 MF의 원리를 딥러닝 모델에 응용해 높은 성능을 낸다.

MBCF의 장점

• 모델 학습/서빙 측면
  • 유저-아이템 데이터는 학습에만 사용되고 학습된 모델은 파라미터와 함께 압축된 형태로 저장된다.
  • 즉, 이미 학습된 모델을 통해 추천하기 때문에 서빙 속도가 빠르다.
• Sparsity / Scalability 문제 측면
  • MBCF는 NBCF에 비해 sparse한 데이터에서도 좋은 성능을 보여, NBCF와 달리 Sparsity Ratio가 99.5%를 넘을 때에도 사용한다.
  • 유저와 아이템의 수가 많이 늘어나도 좋은 성능을 보여 확장성 문제를 개선하였다.
• Overfitting 측면
  • NBCF의 특성상 특정 k개의 이웃에 Overfitting될 수 있는데, MBCF는 전체 데이터의 패턴을 학습하도록 모델이 작동한다.
• Limited Coverage 측면
  • NBCF는 유저-아이템을 많이 공유해야 유사도 값이 정확해지며, 만약 이러한 유사도 값이 정확하지 않은 경우, 정확한 추천 성능을 낼 수 없다.
  • 반면 MBCF는 유사도를 계산하지 않고, 데이터의 내재된 패턴을 학습하여 추천한다.

데이터의 형태 : Explict Feedback vs Implict Feedback

Explict Feedback

• 지난 포스팅의 예제 유저-영화 평점 데이터 처럼 item의 대한 user의 선호도를 직접적으로 알 수 있는 데이터

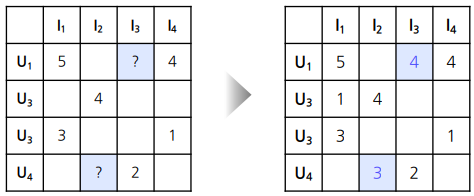
Implict Feedback

• 정확한 Rating이 아닌 클릭 여부, 시청 여부 등 item에 대한 user의 선호들을 상호작용을 통해 간접적으로 알 수 있는 데이터
  • 유저-아이템 간 상호작용이 있었다면 1(positive)를 원소를 갖는 행렬로 표현한다.

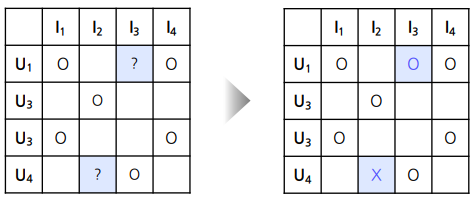
• 현실에서는 implict feedback 데이터의 크기가 훨씬 크고 많이 사용된다.
• Preference : 유저 u가 아이템 i를 선호하는지 여부를 binary로 표현한다.

$f_{ui} = \begin{cases} 1 & r_{ui} > 0 \\ 0 & r_{ui} = 0 \end{cases}$

• Confidence : 유저 u가 아이템 i를 선호하는 정도를 나타내는 increasing function

$c_{ui} = 1 + \alpha \cdot r_{ui}$

• $\alpha$는 positive feedback과 negative feedback 간의 상대적 중요도를 조정하는 하이퍼 파라미터이다.

Latent Factor Model

• MBCF에 활용되는 Model은 Latent Factor Model이다.

Latent Factor Model이란?

• 유저와 아이템의 관계를 잠재적(Latent) 요인으로 표현할 수 있다고 보는 모델이다.
  • 유저와 아이템의 특성을 벡터로 임베딩하여 compact하게 표현한다.
• 유저-아이템 데이터 셋에서 유저-아이템 행렬을 저차원의 행렬로 분해하는 방식이다.
  • 이렇게 분해된 행렬에서의 차원은 모델 학습을 통해 생성되며 차원이 무엇을 의미하는지 알 수 없다.
  • 즉, 같은 벡터 공간에서 유저와 아이템 벡터가 놓일 경우에 유저와 아이템의 유사한 정도를 확인할하는 모델이다.

Singular Value Decomposition(SVD)

• 선형대수에서의 SVD는 차원 축소 기법 중 하나로 분류된다.
• 추천시스템에서 SVD는 Rating Matrix $R$을 유저와 아이템의 잠재 요인을 포함하는 행렬로 분해하는 과정을 말한다.

Full SVD

$R = U\sum V^T$

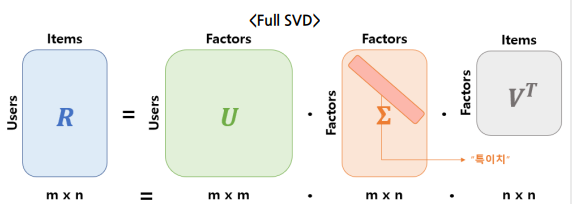
• $U$ : 유저와 Latent Foctor의 관계를 나타낸다.
• $V$ : 아이템과 Latent Factor의 관계를 나타낸다.
• $\sum$ : Latent Factor의 중요도를 나타낸다.
  • $RR^T$을 고유값 분해해서 얻은 대각행렬로, 대각 원소들은 $R$의 singular value(특이치)를 나타낸다.

Truncated SVD

$R \approx {\hat U}\sum_k{\hat {V^T}} = \hat R$

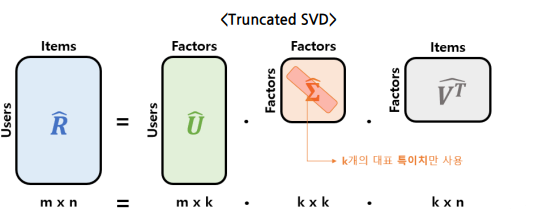
• 대표값으로 사용될 $k$개의 특이치만 사용한다.
• $\hat R$은 축소된 $\hat U, \hat {V^T}, \sum_k$에 의해 계산되며, 분해된 행렬이 부분 복원되면서 가장 중요한 정보로 요약된다는 개념이다.

SVD의 한계

• 대부분 Sparse Matrix인 데이터처럼 분해(Decomposition)하려는 행렬이 Knowledge가 불완전 할 때 정의되지 않는다.
• 따라서 결측된 entry를 Imputation을 통해 Dense Mtrix를 만들어 SVD를 수행한다.
  • 이 때 Imputation은 Computation비용을 높이며, 정확하지 않은 Imputation은 예측의 성능을 떨어뜨린다.
  • 특히 행렬의 entry가 매우 적을 때 SVD를 적용하게 되면 과적합 되기 쉽다.
• 따라서 SVD의 원리를 차용하되, 다른 접근 방법이 필요하다. 이는 Matrix Factoriztion 등장의 배경이 된다.

Matrix Factorization(MF)

MF란?

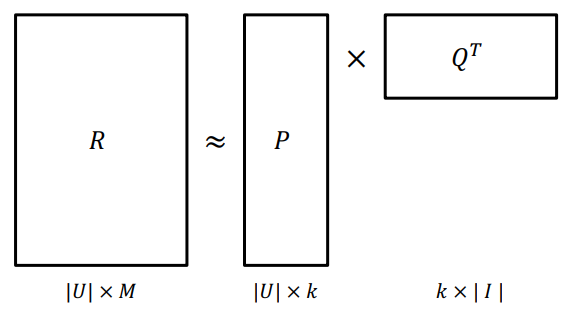
• User-Item 행렬을 저차원의 User와 Item의 latent factor 행렬의 곱으로 분해하는 방법을 말한다.
• SVD의 개념과 유사하지만, MF는 관측된 entry만 모델에 활용해, 관측되지 않은 entry를 예측하는 모델을 만드는 것을 목표로 한다.
• Rating Matrix를 $P$와 $Q$로 분해하여 $R$과 최대한 유사하게 $\hat R$을 추론하도록 최적화한다.

$R \approx P \times Q^T = \hat R$

MF문제 정의

• $R$과 $\hat R$이 최대한 유사하도록 모델을 학습해야 한다.

  $R \approx P \times Q^T = \hat R$

  $P \rightarrow |U| \times k$

  $Q \rightarrow |I| \times k$

• 이를 위해서는 다음과 같은 Objective Function을 정의하고 최적화하는 최적화 문제이다.
  • real-rating : $r_{u, i}$
  • predicted rating : $\widehat{r_{u, i}} = p^T_uq_i$ 일 때
  • Objective Function :
    • $\min_{P, Q}\sum_{\text{observed}\ r_{u, i}}(r_{u, i}-p^T_uq_i)^2$
  • Objective Function with L2-Regularization :
    • $\min_{P, Q}\sum_{\text{observed}\ r_{u, i}}(r_{u, i}-p^T_uq_i)^2 + \lambda(\|p_u\|^2_2 + \|q_i\|^2_2)$
  • Objective Function with L2-Regularization add Bias
    • 시간에 따라 변하는 유저 아이템의 특성을 반영해야 한다. 학습 파라미터가 시간을 반영하도록 모델을 설계하면 다음과 같다.
      • $\widehat{r_{ui}(t)} = \mu + b_u(t) + b_i(t) + p^T_uq_i(t)$
    • $\min_{P, Q}\sum_{\text{observed}\ r_{u, i}}(r_{u, i}-\mu - b_u - b_i -p^T_uq_i)^2 + \lambda(\|p_u\|^2_2 + \|q_i\|^2_2+b^2_u+b^2_i)$
  • Objective Function with L2-Regularization add Bias, Confidence level
    • 모든 평점이 동일한 신뢰도를 갖지 않기 때문에 $r_{u, i}$에 대한 신뢰도를 의미하는 $c_{u,i}$를 추가한다.
    • $\min_{P, Q}\sum_{\text{observed}\ r_{u, i}}c_{u, i}(r_{u, i}-\mu - b_u - b_i -p^T_uq_i)^2 + \lambda(\|p_u\|^2_2 + \|q_i\|^2_2+b^2_u+b^2_i)$
  • $\text{observed }r_{u, i}$ : 실제 관측된 데이터만을 사용해 모델을 학습해야 한다.
    • SVD는 행렬 분해를 위해 결측 entry를 채워 넣었다는 점에서 다르다.

MF 학습

• Loss $L = \sum(r_{u, i}-p^T_uq_i)^2 + \lambda(\|p_u\|^2_2+\|q_i\|^2_2)$
• Error $e_{ui} = r_{ui}-\mu-b_u-b_i-p^T_uq_i$
• Gradient
  • ${\frac {\partial L} {\partial p_u}} = {\frac {\partial(r_{ui}-\mu-b_u-b_i-p^T_uq_i)^2} {\partial p_u} + \frac {\partial\lambda\|p_u\|^2_2} {\partial p_u}} = -2(e_{ui})q_i + 2\lambda p_u = -2(e_{ui}q_i - \lambda p_u)$
  • ${\frac {\partial L} {\partial q_i} = -2(e_{ui}q_i - \lambda p_i)}$
  • ${\frac {\partial L} {\partial b_u} = -2(e_{ui} - \lambda b_u)}$
  • ${\frac {\partial L} {\partial b_i} = -2(e_{ui} - \lambda b_i)}$
• update($\eta = \text{learning rate}$)
  • $b_u \leftarrow b_u + \gamma \cdot (e_{ui}-\lambda b_u)$
  • $b_i \leftarrow b_i + \gamma \cdot (e_{ui}-\lambda b_i)$
  • $p_u \leftarrow p_u + \gamma \cdot (e_{ui}q_i-\lambda p_u)$
  • $q_i \leftarrow q_i + \gamma \cdot (e_{ui}p_u-\lambda q_i)$

Alternative Least Square(ALS)

Basic Concept

• 유저-아이템 매트릭스를 각각 번갈아가면서(Alternative) 업데이트 한다.
  • 즉, 두 매트릭스 중 하나를 상수로 놓고 나머지 하나로 least-square 문제를 품으로서 해당 매트릭스를 업데이트 한다.
• Sparse한 데이터에 대해 SGD보다 더 Robust하며, 대용량 데이터를 병렬처리하여 빠른 학습이 가능하다.

ALS Objective Function considering Implict Feedback

• $\min_{P, Q}\sum_{\text{observed}\ r_{u, i}}c_{u, i}(f_{u, i}-p^T_uq_i)^2 + \lambda(\|p_u\|^2_2 + \|q_i\|^2_2)$

Solution

$p_u = (Q^TC^uQ+\lambda I)^{-1}Q^TC^uf_u$

$q_i = (P^TC^iP+\lambda I)^{-1}P^TC^if_i$

• 이 때 우항의 inverse항을 제거하기 위해 각 항의 왼쪽에 해당 피 inverse항을 곱해주게 되면
  • $(Q^TC^uQ + \lambda I)p_u = Q^TC^ufu$
  • 이는 $A{\bf x} = B$ 꼴이므로, 선형 방정식으로 풀이할 수 있다.
    • 즉 np.linalg.solve를 활용해 한 번에 $p_u$와 $q_i$를 업데이트 할 수 있다.

📚 REFERENCE

• 네이버 부스트캠프 AITECH 5기 강의자료

[추천시스템] Latent Factor Model

https://seing.tistory.com/67