협업 필터링(Collaborative Filtering)

협업 필터링이란?

• 협업 필터링 (Collaborative Filtering, CF)은 많은 유저들로부터 얻은 선호, 기호 정보를 통해 유저의 관심사를 자동으로 예측하는 방법이다.
• 단어 Collaborative의 뜻은 집단적 협업 이라는 뜻으로, CF는 많은 유저와 아이템 데이터가 축적될수록 협업의 효과는 커지고 추천은 정확해질 것이란 가정에서 출발한다.
• 예시
  • 노트북을 본 유저들이 함께 본 다른 상품들 추천
  • 노트북을 구매한 유저들이 구매한 다른 상품들 추천

CF 문제 정의

• 목적
  • 유저 u가 아이템 i에 부여할 평점을 선호도, 클릭 확률 등으로 예측 하는 것
  • 이후 예측 평점이 높은 아이템을 유저에게 추천하는 RecSys의 최종 목적을 달성하는 데 활용된다.
• 방법
  • 주어진 데이터를 활용해 유저-아이템 행렬을 생성한다.
    • 대부분 sparse 행렬이다.
  • 유사도(Similarity) 기준을 정하고, 유저 혹은 아이템 간의 유사도를 구한다.
  • 주어진 평점과 유사도를 활용하여 행렬의 비어있는 값(평점)을 예측한다.
• 원리
  • 특정 유저와 비슷한 취향을 가진 유저들이 선호하는 아이템을 추천 혹은 추천하지 않는 원리이다.
  • 아이템이 가진 속성을 직접적으로 사용하지 않으면서도 높은 추천 성능을 보인다.

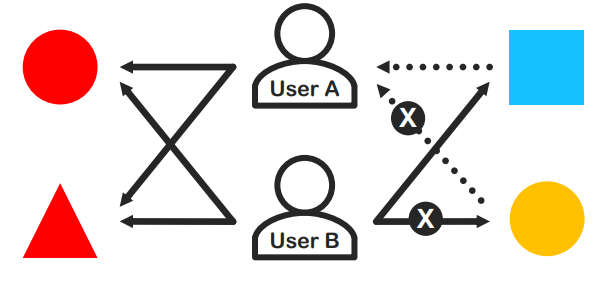
• 분류
  • Collaborative Filtering은 크게 Neighborhood-based CF와 Model-based CF, 이 둘을 Conten-based Recommendation과 결합하여 앙상블하는 방식의 Hybrid CF로 분류된다.

이웃 기반 협업 필터링(Neighborhood-Based CF)

💡 이웃 기반 협업 필터링은 크게 User-Based CF와 Item-Based CF로 나눌 수 있다.

유저 기반 협업 필터링 (User-based CF; UBCF)

UBCF란?

• 두 유저가 얼마나 유사한 아이템을 선호하는지를 구하기 위해 유저간 유사도를 구한 뒤, 타겟 유저와 유사도가 높은 유저들이 선호하는 아이템을 추천하는 방식의 협업 필터링이다.
  

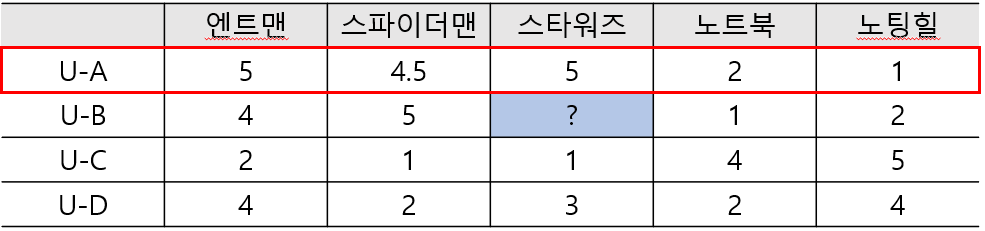
- 직관적으로 B유저는 A유저와 비슷한 취향을 가지므로 유저 A, B의 유사도가 높다.
- 따라서 B유저의 스타워즈에 대한 평점은 A유저처럼 높을 것으로 예측하는 방식이다.

아이템 기반 협업 필터링 (Item-based CF; IBCF)

IBCF란?

• 두 아이템이 유저들로부터 얼마나 유사한 평점을 받았는지를 기반으로 아이템간 유사도를 구한 뒤, 타겟 아이템과 유사도가 높은 아이템 중 선호도가 큰 아이템을 추천하는 방식의 협업 필터링이다.
  

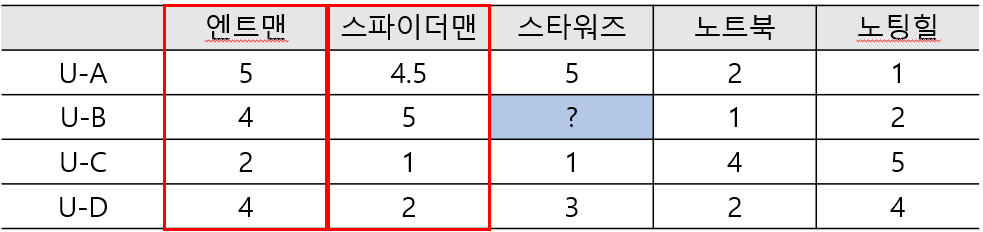
- 직관적으로 스타워즈는 엔트맨, 스파이더맨과의 유사도가 높다.
- 따라서 유저 B의 스타워즈에 대한 평점은 엔트맨, 스파이더맨처럼 높을 것으로 예측하는 방식이다.

NBCF 문제 정의

최종 목적

• 유저 u가 아이템 i에 부여할 평점을 예측하는 것이다.

특징

• 구현이 간단하고 이해가 쉽다는 장점이 있다.
• 아이템이나 유저가 계속 늘어날 경우 확장성이 떨어진다. (Scalability)
• 주어진 평점/선호도 데이터가 적을 경우, 성능이 저하된다. (Sparsity)
• 위 두 가지 문제점은 모든 RecSys에서 풀어야 하는 문제이다.

Sparsity

• 주어진 데이터를 활용해서 NBCF를 통해 유저-아이템 행렬을 만들게 되면 실제 대부분의 원소는 비어있다. (sparse matrix, 희소 행렬)
• NBCF를 적용하려면 적어도 sparsity ratio(행렬 전체 원소 중 비어 있는 원소의 비율)가 99.5%를 넘지 않는 것이 좋다.
  • 그렇지 않을 경우 모델 기반 CF를 사용해야 한다.

K-Nearest Neighbors CF(KNN CF)

KNN CF

등장 배경

• NBCF를 활용해 아이템 $i$에 대한 평점을 예측하기 위해서는 아이템 $i$에 대해 평가를 한 유저 집합 $\Omega_i$에 속한 모든 유저와의 유사도를 구해야한다.
• 유저가 많아질 경우 계속해서 연산량은 늘어나고, 오히려 성능이 떨어지는 NBCF의 한계를 극복하기 위해 등장한 협업 필터링이다.

Key-idea

• $\Omega_i$에 속한 유저 가운데 유저 $u$와 가장 유사한 $K$명의 유저(KNN)를 이용해 평점을 예측한다.
  • example. 1-NN CF (K=1)
    

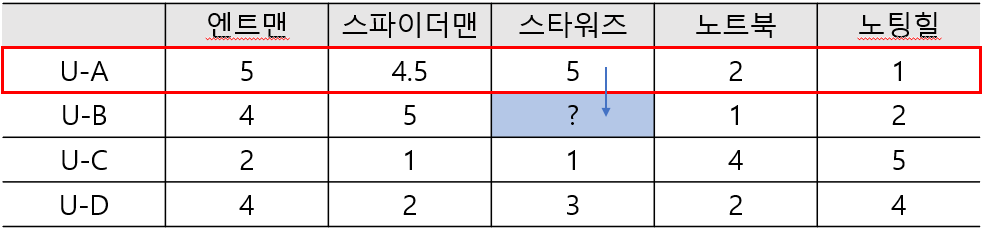
- 유저 B와 가장 유사한 1명의 유저 A 평점 데이터를 이용해 유저 B의 평점을 예측한다.
    - 유저 B의 스타워즈에 대한 예측 평점은 5가 된다.

• 보통 $K$는 25~50을 많이 사용하지면 직접 튜닝해야하는 파라미터이다.
• 유사하다는 것은 정의한 유사도 값이 크다는 것을 의미한다. → 그렇다면 유사도는 어떻게 구할 수 있을까?
  

Similarity Measure

유사도 측정법(Similiarity Measure)

• 두 개체 간의 유사성을 수량화 하는 실수 값 함수 혹은 척도를 의미한다.
• 일반적으로 거리의 역수 개념을 사용해 거리가 가까우면 유사도가 크도록 사용한다.

Mean Squared Difference Similarity

• 주로 RecSys에서 많이 사용되는 유사도 측정 기법이다.
• 각 기준에 대한 점수의 차이를 계산하며, 유사도는 유클리드 거리에 반비례한다.

$msd(u, v) = {\frac {1} {|I_{uv}|}}\cdot{\sum_{i \in I_{uv}}\left(r_{ui}-r_{vi}\right)}^2$ $msd\_sim(u, v) = {\frac {1} {mas(u,v)+1}}$

$msd(i, j) = {\frac {1} {|U_{ij}|}}\cdot\sum_{u \in U_{ij}}\left(r_{ui}-r_{uj} \right)^2$ $msd\_sim(i, j) = {\frac {1} {msd(i, j)+1}}$

• 분모가 0이 되는 것을 방지하기 위해 분모에 1이 더해져 smoothing을 준다.

Cosine Similarity

• 주어진 두 벡터 $\bf x, y$에 대해 두 벡터의 각도를 이용하여 구할 수 있는 유사도이다.
  • 두 벡터의 차원이 같아야 유사도를 계산할 수 있다.
• 직관적으로 두 벡터가 가리키는 방향이 얼마나 유사한지를 의미하며, 방향이 비슷할수록 1에 가깝고 정반대일 경우 -1에 가깝다.

$\cos(\theta) = \cos({\bf x, y}) = {\frac {\bf x \cdot y} {\bf |x||y|}} = {\frac {\sum^N_{i=1}{{\bf x}_i}{\bf y}_i} {\sqrt{\sum^N_{i=1}{\bf x}^2_i}\sqrt{\sum^N_{i=1}}{\bf y}^2_i}}$

Pearson Similarity(Pearson Correlation)

• 주어진 두 벡터 $\bf x, y$에 대해 각 벡터를 표본평균으로 정규화한 뒤에 코사인 유사도를 구한 값이다.

$\text{pearson\_sim}({\bf x, y}) = {\frac {\sum^N_{i=1}\left({{\bf x}_i}-{\bf \bar x}\right)\left({\bf y}_i-{\bf \bar y}\right)} {\sqrt{\sum^N_{i=1}\left({\bf x}_i - {\bf \bar x}\right)^2}\sqrt{\sum^N_{i=1}}\left({\bf y}_i-{\bf \bar y}\right)^2}}$

• 직관적으로 해석하면 ($\bf x, y$가 함께 변하는 정도) / ($\bf x, y$가 따로 변하는 정도)이며, 1에 가까우면 양의 상관관계, 0인 경우 서로 독립, -1에 가까울수록 음의 상관관계를 나타낸다.
• 대게 무난한 추천성능을 보이는 유사도 측정법이다.

Jaccard Similarity

• 주어진 두 집합 A, B에 대해 집합의 개념을 사용한 유사도이다.

$J(A, B) = {\frac {|A\ \cap \ B|} {|A\ \cup\ B|}} = {\frac {|A\ \cap \ B|} {|A| + |B| -|A\ \cap \ B|}}$

• Cosine, Pearson 유사도와 달리 길이(차원)이 달라도 이론적으로 유사도 계산이 가능하다.
• 두 집합이 같은 아이템을 얼마나 공유하고 있는지를 나타내며, 두 집합이 가진 아이템이 모두 같으면 1, 겹치는 아이템이 하나도 없으면 0의 값을 가진다.