AWQ: Activation-aware Weight Quantization for On-Device LLM Compression and Acceleration (CoRR 2023)

Summary

• on-device LLM:
  • 가상비서, 챗봇, 자율주행차량 등에 적용
  • 장점: cloud computing cost를 줄이고 user privacy를 보호할 수 있음
  • 단점: LLM의 model size와 hardware resource사이의 간극이 있어 deployment가 힘듦 (175B GPT-3 $\rightarrow$ 350GB in FP16)
• LLM 크기를 줄이려는 이전의 노력들
  • quantization-aware training (QAT): high training cost
  • post-training quantization (PTQ): low-bit setting에서 performance degradation
  • GPTQ: reconstruction 시 calibration 과정에서 overfit 발생, OOD domain에서 performance degradation
    • additional training이 필요 없다는 것은 장점
    • 하지만 2번에 걸친 보정 때문에 overfit
  • "weights are not equally important for LLM's performance", 대신 0.1-1% 가량의 핵심적인(salient) weight이 있다는 것이고, salient weight만 quantization을 피하면 quantization loss가 줄어들 것
    • 하지만 salient weight을 어떻게 검출할 것이냐?
    • salient weight을 찾아낸다 하더라도 mixed precision인데?
• 본 논문에서는 Activation-aware Weight Quantization (AWQ) 를 제안
  • hardware에 맞춘 LLM의 low-bit weight-only quantization임
• Approach
  • salient weight을 이용하되, '잘' 찾아내고, (salient weight을 사용할 때 발생하는) hardware inefficiency를 극복하자
• Method
  • salient weight을 찾기 위해 weight distribution 대신 activation distrubtion을 이용
  • mixed precision을 보완하기 위해 salient weight scsaling up 후 quantization행
  • 위와 같이 quantization error를 최소화하기 위해 optimal scaling이 가능한 per-channel scaling method를 디자인함
• Experiments
  • LLM과 LMM에 대해 실험 진행: baseline outperform & generalizability
  • calibration set에 대한 generalizability 실험
  • TinyChat을 만들어 실제 on-device에서의 성능을 체크

AWQ: Activation-aware Weight Quantization

Improving LLM Quantization by Preserving 1% Salient Weights

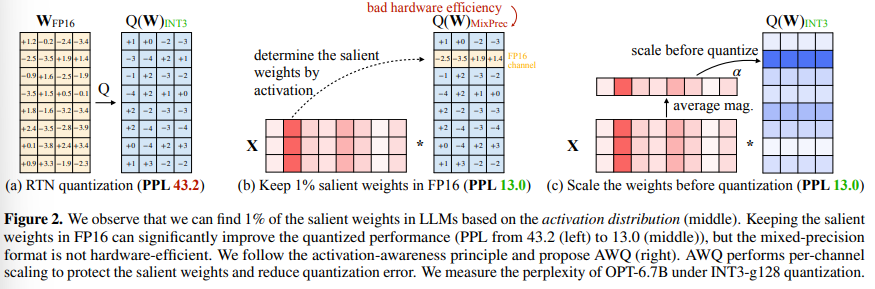
• LLM performance에 있어서 모든 weight가 동등하게 중요하지 않다: 많은 quantization method (e.g. LLM.int8()) 에서 적용하고 있긴 하다만..
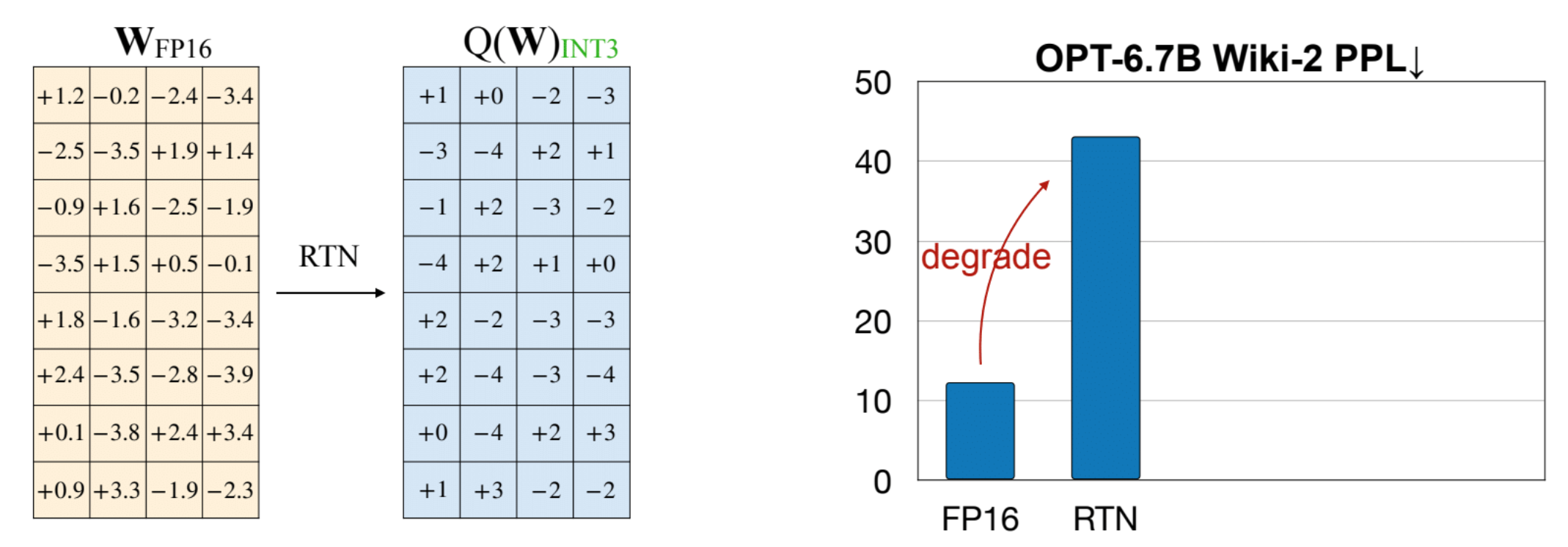
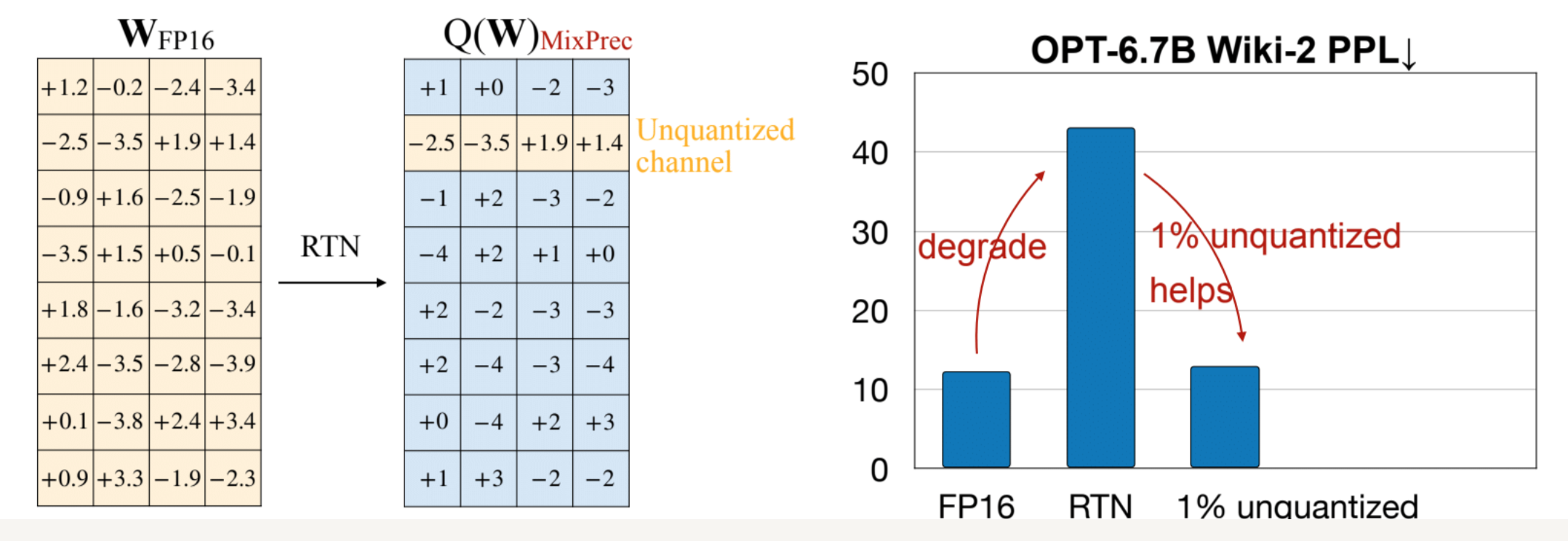
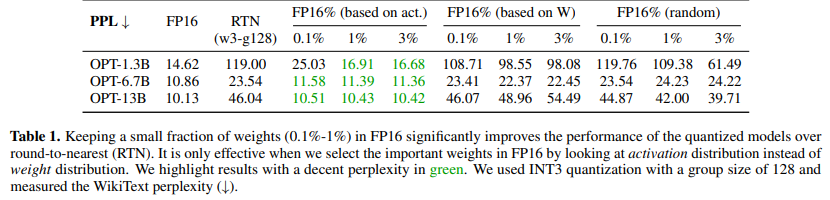
  • 아래에서 naiive하게 Round-to-Nearest (RTN) 하면 성능이 박살나지만, parameter를 1%만 살리면 (FP16) 성능이 복구되는 것 확인

• 중요한 weight인지 어떻게 판별할 것인가?
  • weight의 magnitude를 기준으로 판단 (L2 norm으로 계산): 과연 옳은가?
  • 본 연구진은 weight의 L2 norm (magnitude) 대신 activation magnitude를 기준으로 salient weight임을 판단: activation이 크다면, 중요한 feature일 것

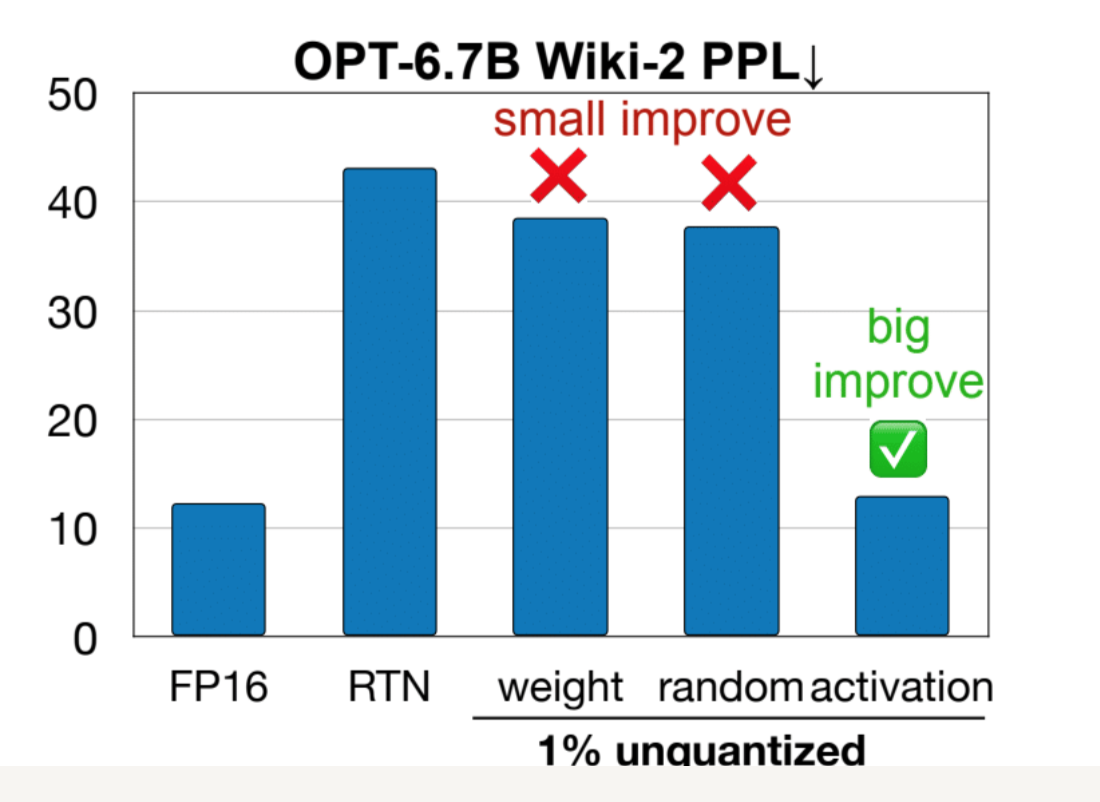
• 위 가설을 검증하기 위해 아래와 같은 실험 진행
  • weight magnitude 기준, random selection 기준으로는 RTN 보다 약간의 성능 향상만 있을 뿐
  • activation magnitude를 기준으로 salient weight을 선정한 결과, 큰 성능 향상 보임

• limitation:

  • 0.1%의 weight은 보존하는데.. mixed precision data type은 hardware inefficiency가 필연적임
  • 따라서 FP16으로 '따로' 처리하는 대신 다른 방법이 필요

• 덧) Mixed Precision의 step

  • (1) model weight을 FP32로 초기화
  • (2) input은 FP16으로 연산
  • (3) FP16으로 연산하는 중 정밀도 손실 방지 위해 일정 주기마다 model weight을 FP32로 복사해 정밀도 보정
  • (4) Backprop 과정에서 FP16 사용해서 연산 속도 향상
  • (5) 학습이 끝나면 model weight을 FP32로 변환해 저장
  • 딱봐도.. FP32로 갔다가 FP16으로 갔다가.. 같은 weight를 FP32로도 저장하고, FP16으로도 저장하는 것은 당연히 hardware inefficiency

Protecting Salient Weights by Activation-aware Scaling

hardware inefficiency issue에서 자유로운 per-channel scaling을 제안
salient weight에만 scaling factor $s$를 적용하여 salient weight을 quantization에서 영향을 덜 받도록 하는 것

e.g. 원래 cahnnel-wise weight가 [1, 1.5] 일 때, 여기에 scaling factor s 10를 곱하면 [10, 15]가 되겠음 $rightarrow$ quantization했을 때 quantized 정수와 원래의 수가 유사해진다

Analyzing Quantization Error

• 흐름: scaling했을때 quantization error에는 문제 없다, 다만 salient weight에만 scaling factor가 적용되므로 non-salient factor와도 고려를 해야 한다!
• 우선, quantization function을 살펴보자

$y=wx$, $y=Q(w)x$
$Q(w)=\Delta \cdot Round(\frac{w}{\Delta})$, where $\Delta=\frac{max(|w|)}{2^{N-1}}$

$N$은 quantization bit 숫자를 의미
$\Delta$는 quantization scaler를 의미 (absolute maximum value에 따라 결정)

• quantized formula를 weight element 차원에서 재구성하면 아래와 같음

$y=Q(w)x \approx Q(\omega \cdot s) \cdot \frac{x}{s}$
$Q(w)=\Delta \cdot Round(\frac{w}{\Delta})$ (equation 1)
$Q(\omega \cdot s) \cdot \frac{x}{s} = \Delta ' \cdot Round(\frac{\omega s}{\Delta '})\cdot x \cdot \frac{1}{s}$ (equation 2)

• $x$는 input value를 의미
• $\omega \in w$, $\omega$는 weight element를 의미
• $s$를 salient weight에 곱해주어 quantization되더라도 weight이 사라지는 것을 막음; 단, $x$에 $s$를 나눔으로써 activation은 유사함
• $\Delta '$는 $s$를 적용한 새로운 quantization scaler (matrix 차원과 달리 $\frac{1}{s}$항이 추가로 곱해지므로 $\Delta$와 $\Delta '$은 달라짐

• 위 식을 적용했을때 empirical 하게 알 수 있는 것들은 다음과 같음

  • (1) $Round(\cdot)$에서 발생하는 error $RoundErr(\cdot)$ 는 equation 1이나 equation 2에서 동일하게 발생
    • round function (반올림) 이 float를 integer로 변환하므로 error는 [0, 0.5] 사이에 거의 균일하게 분포하고, error average는 [0.25] 에 가까움 ($RoundErr(\cdot) \sim 0.25$)
  • (2) element $\omega$를 scale-up하는 것은 matrix $w$의 maximum value에 영향을 주지 않음 (근거를 제시했다면 좋았을 텐데..)
    • 따라서, $\Delta ' \approx \Delta$ 이해가 되지 않는다면, $\Delta=\frac{max(|w|)}{2^{N-1}}$ 를 상기할 것
  • (3) $\Delta$와 $x$는 FP16이므로 quantization error 가 없음

• 따라서, quantization error는 다음과 같이 표현될 수 있음

$Err(Q(\omega)x)=\Delta \cdot RoundErr(\frac{\omega}{\Delta}) \cdot x$
$Err(Q(\omega \cdot s)\frac{x}{s})=\Delta ' \cdot RoundErr(\frac{\omega s}{\Delta '}) \cdot x \cdot \frac{1}{s}$

• scaling factor $s$가 적용된 quantization error의 영향
  • original error($Err(Q(\omega)x)$)에 대한 new error($Err(Q(\omega \cdot s)\frac{x}{s})$)의 비율은 $\frac{\Delta '}{\Delta} \cdot \frac{1}{s}$
  • $\Delta ' \approx \Delta$ 이고, scaling factor $s > 1$ 이므로, salient weight element의 relative error는 작을 것임
• 위 relative error가 작아진다는 것을 증명하기 위해 OPT-6.7B에 대해 실험을 진행 (salient channel은 1%로 설정)

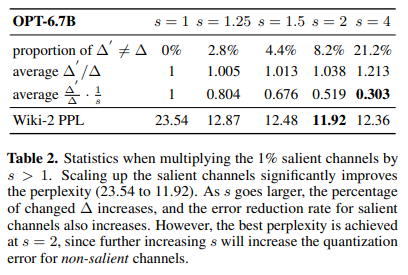
• scaling factor $s$가 늘어날 때 relative error of salient weight element (average $\frac{\Delta '}{\Delta} \cdot \frac{1}{s}$) 은 줄어드는 반면, 일반 weight element의 relative error (average $\frac{\Delta '}{\Delta}$)는 늘어나는 것을 확인 가능
  • 일반 weight element의 relative error가 늘어나면 성능 하락에 영향을 끼치므로, salient weight에 영향을 미치는 scaling factor $s$ 의 적정 수치를 2로 설정할 수 있겠음

Searching to Scale

• optimal scaling factor $s$를 찾는 과정

• 원래 loss는 아래와 같음

  $s*=argmin_sL(s)$
  $L(s)=||Q(W \cdot diag(s))(diag(s)^{-1} \cdot X) -WX||$

  원래의 값($WX$)과 Quantized 값($Q(\cdot)$) 사이의 오차를 줄이는 s

• 하지만 quantization은 not differentiable하므로 근사를 통해 optimal $s$를 찾을 수밖에 없음

  $s=s_{x^{\alpha}}$
  $\alpha^* = argmin_{\alpha}L(s_{x^{\alpha}})$

  $s_x$를 activation magnitude의 avg라고 할 수 있음
  $\alpha$는 hyperparameter

• 실제 $\alpha$는 [0, 1] 사이에서 grid search로 찾는다고

• advantages

  • 추가적인 학습이 필요없음
  • dataset이 조금만 필요함 (activation magnitude avg 계산에 필요) $rightarrow$ 따라서 overfit 없음

TinyChat: mapping AWQ onto Edge Platforms

• TinyChat에서 실제 AWQ의 효용을 확인: 실제 on-device에서 확인 한 것 같은데..?
• Context Understanding stage보다 Generation stage에서 필요한 시간이 굉장히 큼
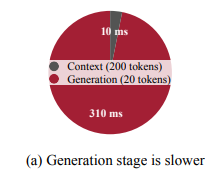
• generation stage는 computational budget보다 memory에 더 bound됨
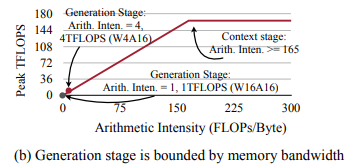
  • arithmetic intensity: ratio of FLOPs to memory access
  • generation stage에서 intensity가 1에 근접: on-device 환경에서는 computation budget보다도 memory access가 중요함
• Weight access dominates memory traffic
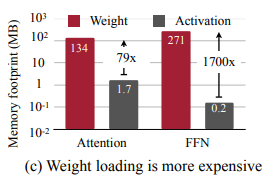
  • memory를 더 많이 잡아먹는 것은 weight와 activation 중 weight: 따라서 weight를 줄이는 것이 더 중요하겠음

Experiments

Settings

• Quantization
• Models: LLM (LLaMA, OPT, Vicuna), VLM (OpenFlamingo-9B, LLaVA-13B)
• Evaluation method: perplexity
• Baselines: Round-to-Nearest Quantization (RTN), GPTQ

Evaluation

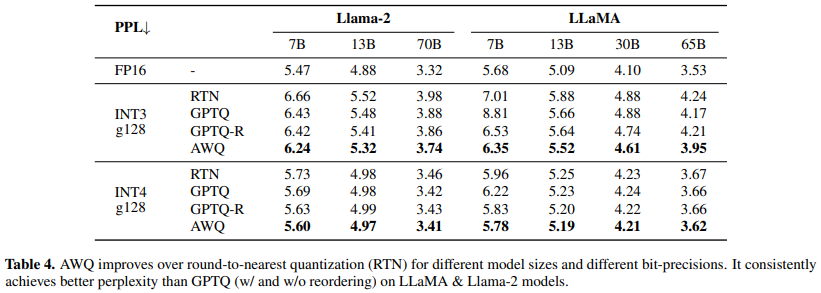
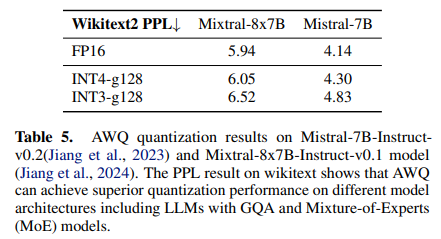
• LLaMA, Mistral & Mixtral에서 superior performance 기록 (Mistral family는 baseline과의 비교가 없는데..?)

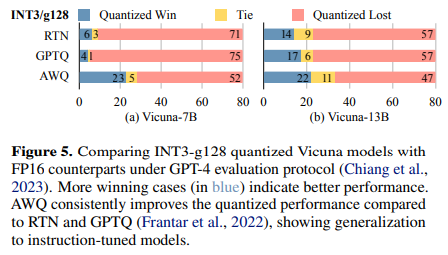
• AWQ는 instruction tuned model (Vicuna) 에서도 효과적임 (다른 baseline들보다는)

• VLM 및 LMM에서도 효과적이어서 generalizability가 있음

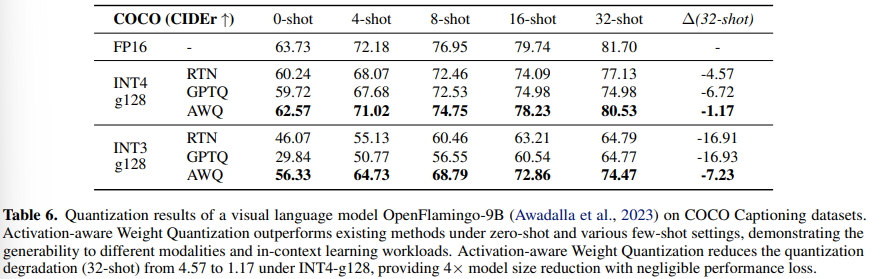
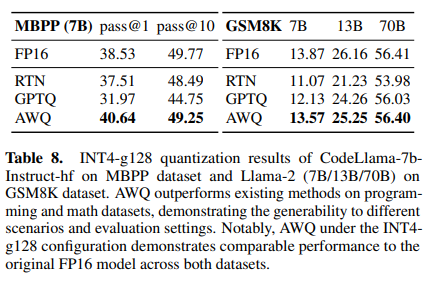
• code & math task에서도 효과적

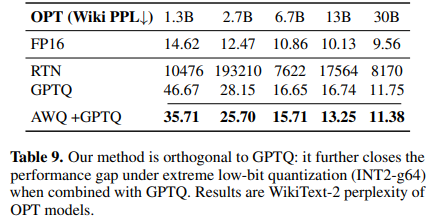
• Int2와 같은 극한 환경 하에서도 잘 작동함 when combined with GPTQ

Data Efficiency and Generalization

• GPTQ (당시 SoTA) 와 비교할 때, calibration set이 훨씬 적음 (약 10%)

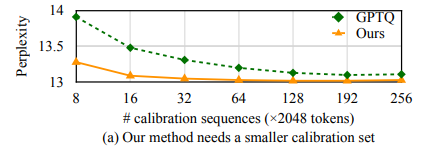
• calibration set에 대해 less sensitive: GPTQ는 sensitive해서 o됨

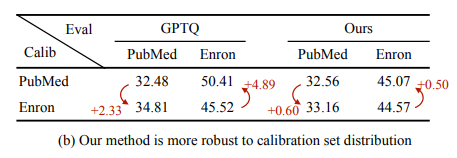
• 실제 on-device (TinyDChat) 에서도 잘 작동: 최대 3.1배 가량의 inference speed

Conclusion

• 모든 weight이 중요한 것은 아니라는 관찰 위에 activation-aware quantization을 쌓아올림

• 장점: 기존 방식과 대비해 salient weight의 quantization error가 줄어들면서도, calibration을 위한 dataset이 적게 필요함

• 실험결과: baseline approach를 outperform하면서도 generalizability가 있음

• 상당히 많이 사용되는 quantization임!