[LLM study] 5.4 Memory-Efficient Model Adaptation

Minhan Cho·2024년 8월 18일

memory efficient model adaptation이란?

inference 시 LLM의 크기가 너무 커서 real-world에 적용하기가 너무 힘듦
$\rightarrow$ memory-efficient approach는 resource-limited setting에서 LLM을 적용함으로써 inference latency를 줄이는 것을 목표로 함

Background of Quantization

무엇을 quantize?: "weights (model parameters)" 또는 "activations (hidden activations)"
- weights: model parameters
- activation: e.g. $y=ReLU(Wx+b)$ 의 output y
어떻게 quantize?:
- floating-point number에서 integers (e.g. 8-bit int) 로
  - 지수: "얼마나 큰 수를 표현 가능하냐?" + 가수: "얼마나 수를 정확하게 표현 가능하냐?"
  - BF16: 부호 1bit + 지수 8bit + 가수 7bit
    LLM의 activation에서 outlier가 발생하므로, FP16만으로는 한계가 있음 (단, FP16보다는 lower precision)
  - FP32: 부호 1bit + 지수 8bit + 가수 23bit
  - FP16: 부호 1bit + 지수 5bit + 가수 10bit
- equation:
  $x_q = R(x/S)-Z$
  - $S$ : scaling factor
  - $Z$ : zero-point factor
  - $R(\cdot)$ : rounding operation
- 실제 예시: $x_{FP32}=$ 1.0 $\rightarrow$ $x_{Int8} =?$
  - 변환코자 하는 값 $x$ in FP32 가 $-1.5 \leq x \leq 2.5$ 이라 하자 (실제 model parameter 의 분포를 고려)
  - Int8의 범위는 [-128, 127] 이므로, scaling factor $S$ 의 계산은 아래와 같음
    
    $S = \frac{Max(x)_{FP32}-min(x)_{FP32}}{Max_{Int8}-min_{Int8}}$
    $S = \frac{2.5-(-1.5)}{127-(-128)}=0.015625$
  - zero point $Z$ 는 $x_{FP32}$ 가 0일 경우, Int8에서 어떤 숫자에 대응되는지를 의미하는 것임
  - zero point $Z$ 는 아래와 같이 계산됨
    $Z=R(min_{Int8}-min(x)_{FP32}/S) =R(-128-(-1.5/0.015625)) = -32$
    - 따라서, $x_{FP32} = 0$ 일 경우, 이를 INT8로 옮기면 -32가 될 것임
    - 만약 $x$ 의 범위가 symmetric ([-2.0, 2.0])이라면 zero point $Z$ 는 0
  - 최종적으로 $x_{FP32}=1.0$ 일 때, $x_{Int8}$ 의 계산은 아래와 같음
    
    $x_{Int8} = R(x_{FP32}/S)-Z$
    $x_{Int8} = R(1.0/0.015628)-(-32)=96$
- What if $x_{FP32}=1.5$ ?
  - 위 식을 계산하면 $x_{Int8}=128$ 로, Int8의 범위 ([-128, 127]) 를 벗어남!
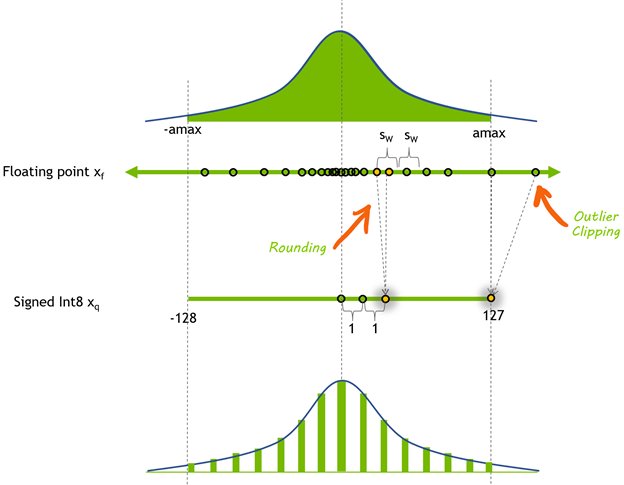
  - 따라서, quantization clipping range [ $\alpha, \beta$ ]를 설정하여 S를 계산
    
    $S = (\beta - \alpha)/(Max_{Int8}-min_{Int8})$
  - $[\alpha, \beta]$ 는 static or dynamic 하게 설정 가능하며, quantization 성능에 큰 영향을 미침 (real world data에 맞춰야 (calibrate) 함)
- Dequantization: $\tilde{x}=S\cdot (x_q + Z)$
  - $R(\cdot)$ 의 역산이 불가능하기 때문에 original value $x$ 와 dequantized value $\tilde{x}$ 사이의 이격이 발생: quantization error

Analysis & Findings on Quantizing LLMs

int8 quantization이 LLM에서 꽤 좋은 performance를 기록할 수 있고, int8보다 낮은 quant는 specific method를 적용해야 함
- Int8 Quant 정도는 상당히 괜찮고, Int4, Int3 등 더 낮은 수준의 quant 를 사용하려면 layerwise method, activation-aware scaling 등이 추가적으로 필요
- LM의 크기가 커질수록 quantization에 둔감: 60GB LLM 4-bit가 30GB LLM 8-bit보다 나음
- 4-bit의 경우, ICL, CoT, instruction following 등 능력은 보존하고 있으므로 고려해볼 만함
weight quant보다 activation quant가 더 어려움
- 6.7B 이상의 LLM에서는 activation의 outlier가 있어서 quant하기가 곤란
- activation quant는 8bit 보다 낮추어 성공적인 경우가 거의 없었음
Efficient fine-tuning enhanced quantization를 사용해서 LLM quant의 성능 향상을 노리자
- LLM quant로 하락할 수 있는 gap을 LoRA, QLoRA 등으로 벌충 가능
- task specific ability 보완 가능
일단 int8, int4의 성능과 소요시간을 보고 둘 중 하나 고르기 (둘 다 FP16과 성능은 유사)

Quantization Methods for LLMs

Quantization-aware training (QAT) 와 Post-training quantization (PTQ) 로 양분됨
- QAT: 추가적인 training 필요
- PTQ: model retraining 불필요 (LLM quantization에 주로 사용)

PTQ

Mixed-precision decomposition
- emergence of outliers: 이상하게 너무 큰 value가 hidden activation에서 나와요!
- 그런데 이 outlier마저도 의미가 있으므로, outlier는 16BF로 처리하고, 나머지는 8-bit int로 처리하자는 것
Fine-grained quantization
- quantization error를 줄여보고자 하는 시도 (e.g. ZeroQuant)
Balancing the quantization difficulty
- activation보다 weight이 더 quantize하기 쉽다며? 그럼 activation quantization 할 때의 difficulty를 weight로 migrate하자 (e.g. SmoothQuant)
Layerwise quantization
- layerwise reconstruction loss ( $argmin_{\hat{W}}||WX-\hat{W}X||^2_2$ 를 적용해 optimal quantized weight을 계산
- OBQ, GPTQ, AWQ 등