DMTP: A Deep Meta-Learning Based Framework for Mobile Traffic Prediction (IEEE Wireless Communications 2021)

Minhan Cho·2023년 9월 5일

Time Series Prediction Traffic Network

Key Points

본 연구는 최적의 hyperparameter (input sequence length $SN$ ) & parameter $P$ 을 찾아내는 meta-learner 를 만드는 것임
meta-learner
- input: traffic network 를 FFT 로 뽑아낸 frequency component vector
- output: optimal $SN$ & parameter $P$ in vector form
- model: more than 3-layer MLP
base-learner
- input: sequence vector (normalzied mobile traffic load, 요일, hour)
- output: next time step 의 normalized mobile traffic load
- model: multiple LSTM blocks
Finn et al. (2017) 과의 차이
- Finn et al. (2017) 은 model-agnostic, 따라서 어떤 모델이든 해당 모델의 initial parameter 만을 최적화
- 본 연구는 hyperparameter 까지 찾아야 함: time series prediction 의 input 에 사용되는 input sequence length 를 예측
  또한, FFT 를 이용해 network traffic 의 component 를 뽑아냄

misc

SN, 즉 input sequence length 의 길이만큼만 써서 frequency component vector 를 만들어내는 거 아닌가?
그럼 SN = 6 이런 거는 frequency component vector 길이가 굉장히 짧을 텐데 (chatGPT한테 물어보니까 한 vector shape을 바꿀 수는 없다는데) output의 shape 은 429.. 이거 제대로 학습이 되나?
일단 frequency component vector 를 이용(similarity 를 위해)해볼 수 있을듯?

Abstract

Introduction

Dataset Description and Background Knowledge of Meta-Learning

Mobile Traffic Traces

Milan mobile traffic load (9,999 telecom grid), Guangzhou SMS data (2 predictions), London Twitter data (2 predictions) 로 구성 (각각의 grid와 prediction 은 task로 지칭)
위 3개의 dataset 은 모두 다른 characteristics 가짐

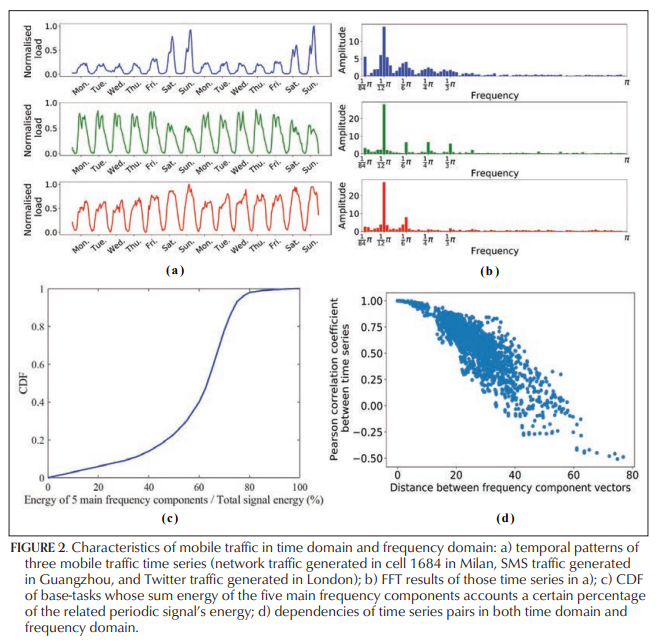
Characteristics of Mobile Traffic

선행연구에 따라, time interval을 1시간으로 둠: 밀라노에서 1시간 단위로 안 두면 0 값이 너무 많다는 듯
peak value 가 데이터에 따라서 5배까지 차이나서 minmax scaling 진행
데이터의 수치 차이가 나긴 하지만 weekly cyclic pattern 있음
주 1개 (Mon-Sun) 의 데이터 뽑아서 Fast Fourier Transform을 이용한 Discrete Fourier Transform 진행
- main frequency: pi/84 (week), pi/12 (day), pi/6 (12 hrs), pi/4 (8 hrs), pi/3 (6 hrs) 로 총 5개
- 전체 task 의 60%에서 위 5개의 main frequency 의 signal energy 의 합이 해당 task의 전체 signal energy 의 60% 를 넘음 (signal energy 가 무엇인지, 어떻게 구하는지는 필요하면 더 찾아보겠음)
각 traffic network 마다 frequency component vector of size 10 를 만들어서 5,000개 random pair 를 구성하여 Euclidean distance 와 Pearson correlation 을 계산
- Euclidean distance 와 Pearson correlation 사이에 음의 상관관계: 비슷한 frequency component 를 갖고 있으면 두 time series 의 시간 도메인 variation 이 비슷함
- traffic pattern prediction task 에 frequency component vector 를 써먹을 수 있음

misc: DFT & FFT

Discrete Fourier Transform (DFT): 보통의 traffic network는 x축이 시간 (이를 시간 도메인이라 함) 으로 이루어져 있으나, 이를 x축이 frequency 인 그래프 (이를 주파수 도메인이라 함) 로 구성하는 것. 이산 신호 (띄엄띄엄 존재하는 데이터, 보통 연속 신호를 샘플링하여 이산 신호를 구성) 의 주파수 성분을 알기 위함임.
Fast Fourier Transform (FFT): Discrete Fourier Transform 을 수행하는 알고리즘. 시간 도메인으로 구성된 플롯에서 파형을 구성하는 사인꼴 신호의 진폭과 주파수를 추정하기 어려우므로, FFT 분석을 통해 파형을 구성하는 사인꼴 신호의 진동수와 진폭을 구할 수 있음.
simple FFT example

import numpy as np
import matplotlib.pyplot as plt

# Generate a sample signal: sum of two sine waves
Fs = 500  # Sampling rate
T = 1/Fs  # Sampling interval
t = np.arange(0,1,T)  # Time vector
f1, f2 = 5, 50  # Frequencies
y = np.sin(2 * np.pi * f1 * t) + np.sin(2 * np.pi * f2 * t)

# Apply FFT
n = len(y)
k = np.arange(n)
T = n/Fs
frq = k/T  # Two sides frequency range
frq = frq[range(n//2)]  # One side frequency range
Y = np.fft.fft(y)/n  # FFT and normalization
Y = Y[range(n//2)]

# Plotting
plt.subplot(2,1,1)
plt.plot(t,y)
plt.title('Generated Signal')
plt.xlabel('Time')
plt.ylabel('Amplitude')

plt.subplot(2,1,2)
plt.plot(frq,abs(Y))
plt.title('FFT: Main Frequency Components')
plt.xlabel('Freq (Hz)')
plt.ylabel('|Y(freq)|')
plt.show()

Meta-Learning (& Notation)

why use meta-learning?
- increase learning efficiency through experience
- goal: understand how learning itself can become flexible according to the domains or tasks
Notation
- $\xi$ : typical supervised learning task
- $\sigma$ : (typical) learner
- typical supervised learning task $\xi$ 와 typical learner $\sigma$ 를 대상으로, 각 sample 은 unknwon target function $F_{\xi}$ 를 이용해 label 됨
- $H_{\sigma}$ : hypothesis space of learner $\sigma$ , 다시 말해 set of all possible hypothesis functions generated by $\sigma$
- $\sigma$ 의 학습과정은 hypothesis function $h_{\sigma}(\xi)$ 를 찾는 것
  이 때, $h_{\sigma}(\xi)$ 는 $\sigma$ 의 hypothesis space ( $H_{\sigma}$ 를 말하는 것 같음, set of all possible hypothesis functions generated by $\sigma$ )에 target function $F_{\xi}$ 를 근사(approximate)시킴
- learner $\sigma$ 는 사용된 learning algorithm, hyperparameters, initial status 등으로 생성된 set of biases 를 embed 함 (어디에?)
- 위의 bias는 base-learner (아마도 learner $\sigma$ 를 의미하는 것일 듯, 뒤를 참조하면 base-learner는 low-level task를 지칭함) 의 hypothesis space 를 제한하는 역할을 하며, base-learner 가 hypothesis space 를 탐색하는 데에 영향을 미침
- meta learning: meta learning 은 base-learner 의 bias를 individual task 에 match 하는 역할을 함, match 과정은 meta task 를 통해 이루어지며 learning task 의 meta-features에 따라 learning task 의 set of biases 를 생성함
- meta task: meta learning 은 meta task 를 통해 이루어지며, meta-learner 가 handle하는 learning task로 해석할 수 있음

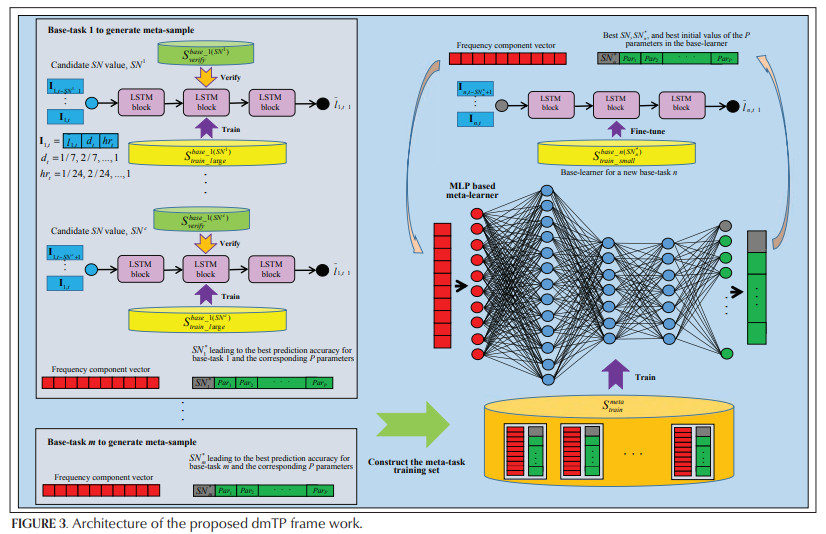
The Proposed DMTP

(Notation cntd.)

base-task: 개개의 mobile traffic prediction task
base-learner: base-task 를 해결하기 위한 LSTM networks
meta-features: base-task (individual mobile traffic prediction task) 의 frequency component vector
set of biases: SN (number of steps, input sequence 의 length), initial values of neural connection weights and neural threholds
- 덧) 그러면 후자는 결국 initial model parameter 를 최적화한다는 건가?
base-learner 의 hypothesis space: linear layer (3 * SN-dim -> 1 * SN-dim)
- SN 의 value 가 base-learner 의 hypothesis space 를 결정
- initial parameter values 는 base-learner 의 initial searching point를 base-learner 의 hypothesis space 안에서 결정함
base task 의 meta feature 가 traffic pattern 의 characteristics 를 반영
- 따라서 base-learner 의 best set of biases 는 해당 task의 meta-features에 영향을 받을 것으로 추정됨
meta learner: MLP layer
- meta learner의 역할 1: base-tasks (개개의 task) 와 best set of bias (SN, initial weights) 사이의 correlation 을 extract 하는 역할
- meta learner의 역할 2: 새로운 base-task의 meta-feature를 참고해서 base-learner의 best set of biases를 뽑아냄

Notations in dmTP

$S^{meta}_{train}$ : meta task training set, meta task training 에 사용될 meta-samples를 만드는 set of base-tasks 임
$S^{base\_m(SN)}_{train\_large}$ : $S^{meta}_{train}$ 의 base-task $m$ 에 대해 large base-task training set of base-samples 을 의미, 이는 $m$ 의 base-learner 학습에 사용
$S^{base\_m(SN)}_{verify}$ : 위와 같은데, valdiation 용도로 사용되는 base-samples, 윗첨자 $SN$ 은 when number of steps equals SN
$S^{base\_n(SN^*_n)}_{train\_small}$ : meta train ( $S^{meta}_{train}$ )에 포함되지 않은 base-task $n$ 에 대해 base-learner 의 fine-tuning 용도로 사용하는 samples 를 의미
$S^{base\_n(SN^*_n)}_{test}$ : test 용도의 base-samples

LSTM Network as the Base-Learner

base-learner로 Q-layer LSTM 구성
input: previous $SN$ time intervals 의 input vectors (normalized mobile traffic load, the day of the week, the hour of the day 로 구성)
output: normalized mobile traffic load of next time interval

Train the Meta-Learner with Meta-Samples

$SN$ value가 적절한 hypothesis space 를 결정 (상단에 보면 원래부터 $SN$ value 가 hypothesis space 를 limit 한다고 나와있음) 하고 initial parameters 가 target 에 근접한다면 base-learner 가 좋은 성능을 나타낼 것
$SN$ value 및 optimal parameter $P$ 의 선정
- $SN$ value는 base-tasks set $S^{meta}_{train}$ 의 각각의 task $m$ 에서 exhaustive trials 를 통해 multiple candidates 에서 뽑힘
- $SN$ value canidate 을 $SN^C$ 라 함
- randomly selected parameters $P$ 와 상기한 $SN^C$ 를 이용하여 $S^{base\_m(SN^C)}_{train\_large}$ 에서 학습하고 $S^{base\_m(SN^C)}_{verify}$ 에서 검증 ( $SN$ value 또는 sequence length 마다 다른 $m$ 에서 돌림)하여 가장 높은 accuracy 를 기록한 $SN$ value 를 $SN_m^*$ 로 기재할 수 있음
- base-task $m$ 의 frequency component vector 를 $SN_m^*$ 로 이름을 붙이고(labelling), 가장 높은 performance 를 보였을 때의 parameter $P$ 의 pair를 하나의 meta-sample로 만듦
meta-learner: at least 3 layers MLP
- $S^{meta}_{train}$ (base-task 집합) 에서 meta-learner 를 학습시킴
- 새로운 base-task n (의 frequency component vector, 원문에서는 명시적으로 나오지는 않았지만 figure 를 참조하면 frequency component vector 를 넣었을 때 $SN^*_m$ 과 optimal parameter $P$ 롤 output 으로 내뱉을 수 있도록 MLP를 학습시킴) 이 들어갔을 때 적절한 $SN_m^*$ 과 parameter $P$ 가 도출될 수 있게끔 함

Fine-Tune the Base-Learner for a New Base-Task

new base-task $n$ 이 주어졌을 때, frequency component vector 를 meta-features 로써 먼저 뽑아냄
meta-learner (MLP) 에 meta-features (frequency component vector) 를 먹여서 optimal sequence length $SN_m^*$ value 와 parameters $P$ 를 뽑아냄
뽑아낸 $SN_m^*$ 와 $P$ 를 base-learner (LSTM blocks) 에 먹여주고 $S^{base\_n(SN^*_N)}_{train\_small}$ 에 대해 finetuing 진행

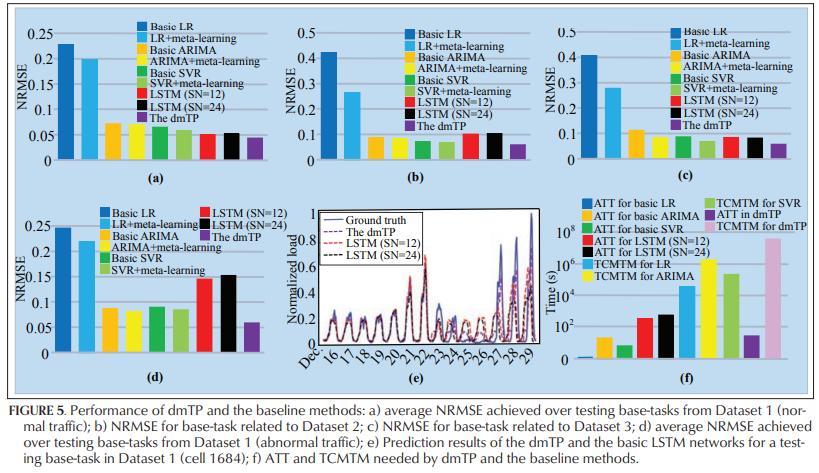
Evaluation on Real-World Mobile Traffic Data

Experimental Settings

base learner
- 3-layer LSTM: 1st layer, 2nd layer 의 output dimension 은 5
- num of parameters: 428
meta learner
- 3-layer MLP: 300, 300, 400
meta training set
- meta-training set $S^{meta}_{train}$ : dataset 1 에서 9999개 task 중 8000개 선택
- $SN$ : base-task 마다 3-24 에 대해서 실험
- $SN^C$ 만큼의 sliding window 만들어서 base task $m$ 의 base-samples 생성, normalized traffic load
- $SN^C$ 만큼의 sequence 로 나눈 base samples 에 대해 90% 를 randomly select 해서 $S^{base\_m(SN^C)}_{train\_large}$ , 다시 말해 training set 을 구축하고 나머지 10%로 $S^{base\_m(SN^C)}_{verify}$ , 다시 말해 validation set 을 구축
meta testing
- meta training에 포함되지 않은 1999개의 base task, dataset 2, dataset 3 를 대상으로 meta testing 진행
- meta-learner 의 output인 $SN_n^*$ 를 sliding window로 써서 base sample을 만듦
baseline models: ARIMA, LR, SVR, LSTM (sliding window 12, 24)
metric: normalized root mean square error (NRMSE)