[논문 리뷰] Neural Collaborative Filtering

정준환·2022년 10월 30일

논문리뷰 추천시스템

논문리뷰

목록 보기

4/5

본 논문을 이해하기 위해서는 아래 항목들에 대한 기초적인 이해가 필요합니다.

Collaborative Filtering (CF)
Neural Networks
Deep Learning
Matrix Factorization (MF)
Implicit Feedback

요약

MF가 잘 되긴 하는데 한계가 있다. Neural Network를 MF에 적용해 non-linear한 경우에도 추천이 가능하도록 해보자.

1. INTRODUCTION

Matrix Factorization(MF)은 오랫동안 추천시스템에서 잘 사용되어온 방법이다. 이 MF를 발전시키기 위한 많은 노력과 방법들 (ex. Factorization Machine)이 있었는데, 결국 큰 틀인 latent feature vector를 단순히 inner product, 내적하는 것에서 벗어나지 못했다. 이는 결국 user와 item 사이의 관계를 linear하게 한정하게된다.

이러한 문제를 해결하기 위해 user, item의 latent feature vector를 inner product가 아닌 Neural Network를 사용해 관계를 나타냄으로써 non-linear한 경우에도 표현할 수 있도록 했다. 이러한 모델을 NCF (Neural network-based Collaborative Filtering) 이라고 한다.

Contribution

NCF의 기본 구조 제시
MF는 결국 NCF의 특별한 케이스임을 보임
NCF가 더 좋음을 실험적으로 증명

2. PRELIMINARIES

2.1 Learning from Implicit data

Implicit data에서는 선호를 알 수 없다. 단순한 상호작용만 기록한다. 식으로 나타내면 아래와 같이 표현할 수 있다.

$M$ : user의 수
$N$ : item의 수
$\bold Y \in \R^{M \times N}$ : user-item 상호작용 (implicit)

y_{ui} = \begin{cases} 1, & \text{if interaction (user $u$, item $i$) is observed} \\ 0, & \text{otherwise} \end{cases}

주의할 점은

1이라고 해서 user가 item을 좋아한다고 확신할 수 없으며
0이라고 해서 user가 item을 싫어한다고 확신할 수 없다.

다만 그러할 확률이 더 높다고는 추측할 수 있다. 따라서 이러한 implicit feedback data를 해석할 때에는 상황에 맞게 분석자의 주관이 개입된다.

어찌되었든, 추천을 하기 위해 $\hat y_{ui}$ 를 구해야 하는데, 수식으로 나타내보면 아래와 같다.

\hat y_{ui} = f(u, i | \Theta) \\

여기서
$\Theta$ 는 model parameters,
$f$ 는 interaction function, 즉 $(u, i, \Theta)$ 를 $\hat y$ 로 mapping 해주는 함수다.

이런 문제는 크게 두가지 방법으로 최적화를 진행할 수 있다.

point-wise
pair-wise

point-wise 방법은 말 그대로 각각 한 점들에 대해서 분석을 진행하는 방법이다. 우리가 가장 익숙한 방법이라고 볼 수 있다.

pair-wise 방법은 두 점을 짝 지어서 두 점 간의 차이를 보는 방법이다. 해당 방법을 모르면 여기를 참고하자. (안읽어도 크게 무리는 없다.)

NCF의 경우, $f$ 가 parameterized 되어 있기 때문에, 두 방법 모두를 지원한다.

2.2 Matrix Factorization

MF에서 model parameter $\Theta$ 는 user latent vector와 item latent vector다. 이를 각각 $\bold p_u, \bold q_i$ 라고 하자. MF에서 $f$ 는 내적이므로 아래와 같이 표현할 수 있다.

\hat y_{ui} = f(u, i | \Theta) = f(u, i | \bold p_u, \bold q_i) = \bold p_u^T \bold q_i = \sum_{k=1}^K p_{uk}q_{ik}

이 내적이 문제다. 아래 그림을 보면서 얘기해보자.

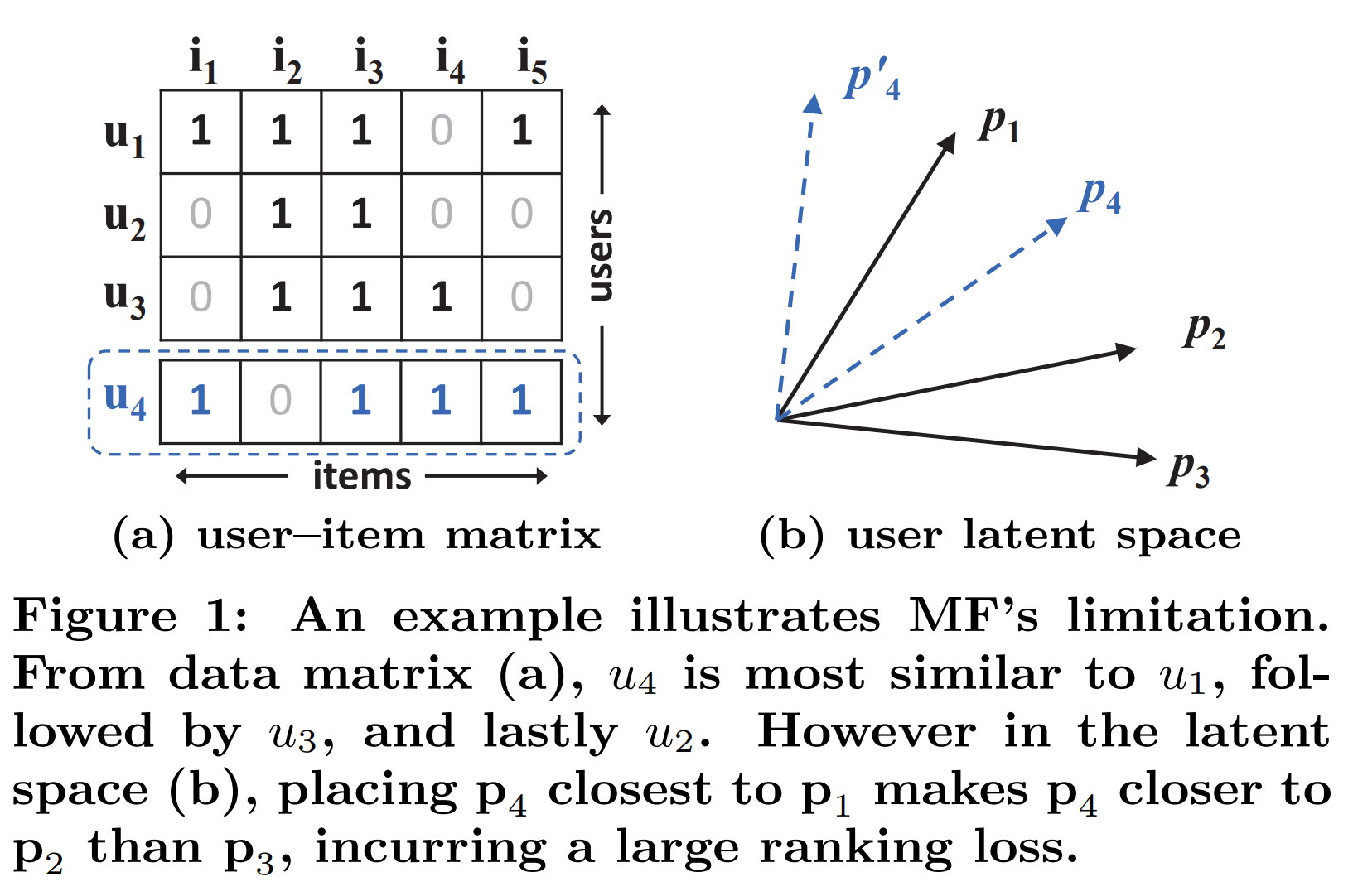
(a)를 보고 user들의 상관관계를 간단한 Jaccard coefficient를 이용해 계산해보자. $(s = \frac{ n(교집합) }{ n(합집합)})$

s_{12} = \frac{2}{4} = 0.5, \qquad s_{23} = \frac{2}{3} = 0.66, \qquad s_{13} = \frac{2}{5} = 0.4

모든 항목에 대해서 계산 해보면 아래 표와 같다.

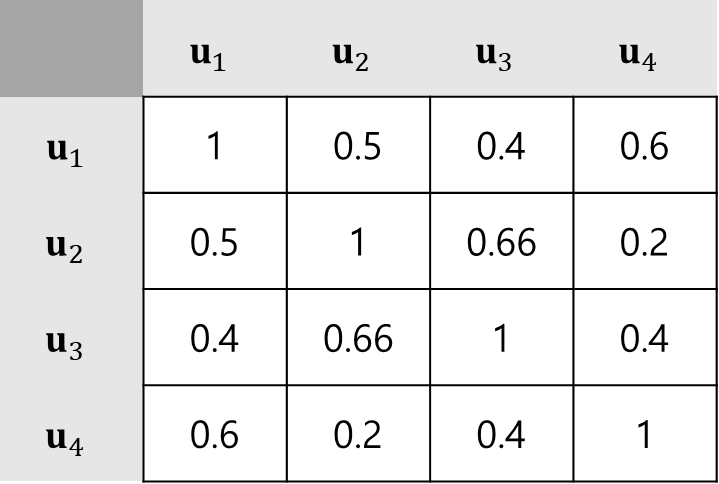
$\bold u_4$ 를 무시하고, 세명의 유저에 대해서 먼저 생각해보자.
$s_{23} > s_{12} > s_{13}$ 이기 때문에, user latent factor를 그려보면 $p_2$ 와 $p_3$ 는 가깝게, $p_1$ 은 $p_3$ 보다는 $p_2$ 에 가깝게 그려야 한다. 이것이 Figure 1의 (b)에 검정색 선으로 잘 그려져 있다.

문제는 $\bold u_4$ 가 등장하면서 나타난다. $\bold u_4$ 는 $s_{41} > s_{43} > s_{42}$ 이기 때문에, $p_4$ 는 $p_1$ 과 가장 가까우며 $p_2$ 와 가장 멀게 그려져야한다. 이는 현재의 차원에서는 그려낼 수가 없다. 물론 latent vector의 차원을 올리면 해결할 수 있는 문제지만, over-fitting등의 문제가 발생하기 쉽다. 따라서 이를 해결하기 위해 Deep Neural Network, DNN의 사용을 제안한다.

3. NEURAL COLLABORATIVE FILTERING

3.1 General Framework

바로 위에서 언급했듯이, 이 MF의 문제를 Neural Network를 사용해서 해결한다. 아래는 이 NCF의 General framework다.

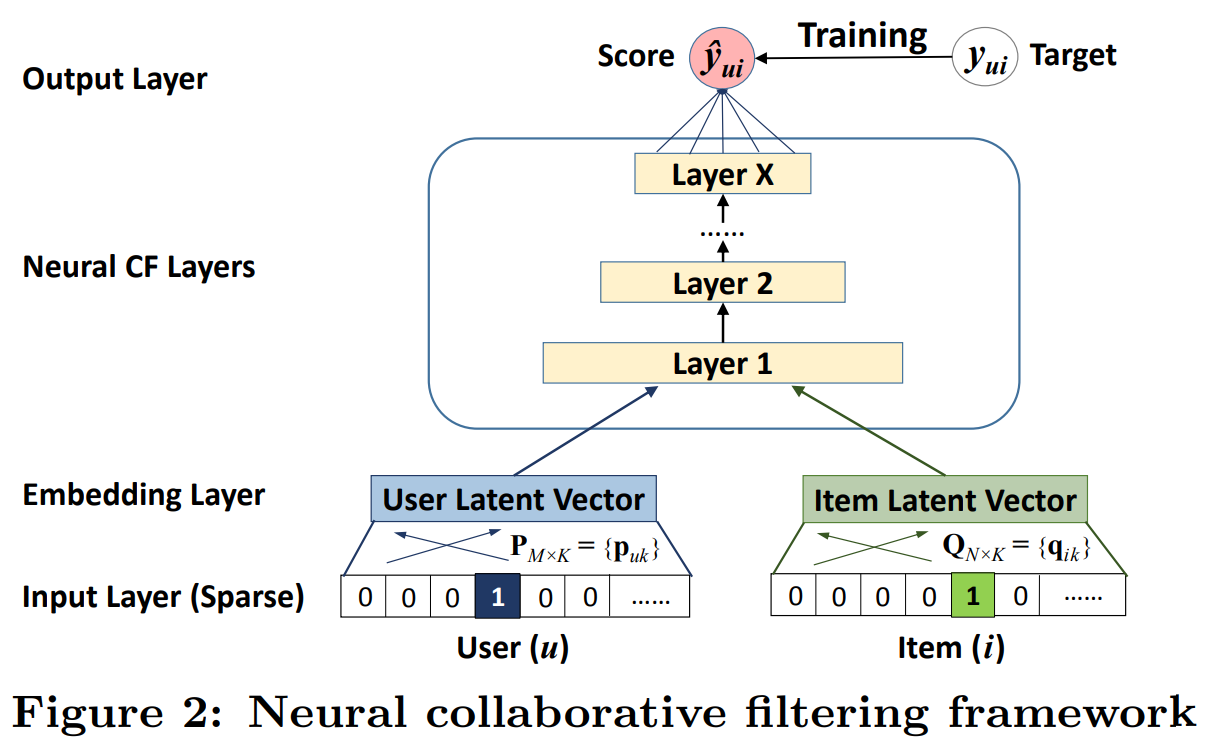
MF와 마찬가지로 user와 item을 특정 차원으로 embedding을 한다. 이후, 단순한 내적이 아니라 Neural CF Layers를 통해 $\hat y_{ui}$ 를 도출해냄을 확인할 수 있다.

위 그림을 수식으로 나타내보면 아래와 같다.

\hat y_{ui} = f(\bold P^T \bold v_u^U, \bold Q^T \bold v_i^I | P, Q, \Theta_f) \tag{3}

여기서

$\bold P \in \R^{M \times K}, \bold Q \in \R ^{N \times K}$ 는 user와 item을 $K$ 차원으로 embedding 해주는 matrix,
$\bold v_u^U, \bold v_i ^I$ 는 user, item의 one-hot vector
$\Theta_f$ 는 함수 $f$ 에 따른 모델의 parameter
$f$ 는 neural network의 layer들

를 의미한다.

$f$ 를 풀어서 써보면 식 (3)은 아래 식(4)로 나타낼 수 있다.

\begin{aligned} \hat y_{ui} &= f(\bold P^T \bold v_u^U, \bold Q^T \bold v_i^I | P, Q, \Theta_f) \\ &= f(\bold P^T \bold v_u^U, \bold Q^T \bold v_i^I ) \\ &= \phi_{out}(\phi_X(...\phi_2(\phi_1(\bold P^T \bold v_u^U, \bold Q^T \bold v_i^I )))) \end{aligned} \tag{4}

여기서 각각의 $\phi_x$ 들은 neural network의 layer들을 의미한다.

3.1.1 Learning NCF

이제 식 (4)를 통해 우리는 NCF의 $\hat y_{ui}$ 를 계산할 수 있게 되었다. 이 값을 $y_{ui}$ 와 비교해 학습을 진행하면 되는데, 간단하게는 MSE, RMSE 등 $y_{ui} - \hat y_{ui}$ 을 이용한 여러가지 방법이 있을 수 있다. 그런데 이런 방법은 앞에서 언급한 특성들로 인해 implicit feedback을 학습하기에는 그리 적당하지 않다. 따라서 본 논문에서는 $\hat y_{ui}$ 를 예측하기 위해 확률적으로 접근하는데, 이는 $\hat y_{ui}$ 가 $0$ ~ $1$ 의 값을 가지므로 확률이라고 분석하는 것이 가능하기 때문이다. $\hat y_{ui}$ 값은 이제 $u, i$ 가 얼마나 상관이 있는지 나타내는 확률값이라고 생각해도 좋다. 논문에서는 해당 likelihood를 아래와 같이 정의한다.

p(\mathcal Y, \mathcal Y^- | \bold P, \bold Q, \Theta_f ) = \prod_{(u, i) \in \mathcal Y} \hat y_{ui} \prod_{(u, j) \in \mathcal Y^-} (1-\hat y_{uj}) \tag{6}

$\mathcal Y$ 는 관측된 값들, $\mathcal Y^-$ 는 관측되지 않은 값들의 집합이다. 위의 식을 해석하자면 $\mathcal Y$ 에 포함된 $u, i$ 에 대한 $\hat y_{ui}$ 는 1에 가까울수록 좋고, $\mathcal Y^-$ 에 대한 $\hat y_{uj}$ 는 0에 가까울수록 좋다는 뜻이다. 위의 식에 로그를 씌워 음수로 처리해주면 우리가 낮춰야 할 loss function을 수치화 할 수 있다.

\begin{aligned} L &= -\sum_{(u, i) \in \mathcal Y} \log \hat y_{ui} - \sum_{(u, j) \in \mathcal Y^-} \log (1- \hat y_{uj}) \\ &= \sum_{(u, i) \in \mathcal Y \cup \mathcal Y^-} y_{ui} \log \hat y_{ui} + (1-y_{ui})\log(1-\hat y_{ui}) \end{aligned} \tag{7}

식 (7)을 보면 결국 cross-entropy와 동일한 형태임을 확인할 수 있다. 이제 이를 SGD와 같은 방법을 이용해서 파라미터들을 최적화하면 모델을 학습할 수 있다.

3.2 Generalized Matrix Factorization (GMF)

NCF라는 것은 결국 MF에서의 내적을 Neural network로 치환한 진화버전이다. 그렇다면 NCF에서 layer가 내적을 계산한다면, 결국 이는 기존의 MF와 다를바 없다. 식 (4)의 $\phi_x$ 가 내적을 계산해준다고 생각하면된다. $\phi_1(\bold p_u, \bold q_i) = \bold p_u \odot \bold q_i$ 처럼 표현할 수 있겠다.

즉, MF는 NCF의 특별한 하나의 케이스라고 생각할 수 있으며, 이를 GMF라고 명명했다. 이를 왜 따로 언급하는지는 뒤에서 설명한다.

3.3 Multi-Layer Perceptron (MLP)

위의 GMF는 layer가 굉장히 특수한 케이스다. 이에 반해 MLP는 우리가 일반적으로 생각하는 Neural network의 구조를 가진다. 여러개의 층이 있고, ReLU, sigmoid등의 non-linear activation function을 활용한다. 본 논문에서는 ReLU를 사용했다.

3.4 Fusion of GMF and MLP

앞서 3.2 Generalized Matrix Factorization (GMF)와 3.3 Multi-Layer Perceptron (MLP)에서 굳이 두가지의 경우를 언급한 이유가 여기있다.

1. INTRODUCTION 에서 언급했듯, MF는 non-linear한 경우 제대로된 예측이 힘들다는 단점을 가지고 있다. 그럼에도 불구하고 오랜시간 추천시스템에 잘 사용되어 왔다는 뜻은, 반대로 생각하면 linear한 경우 예측을 잘 한다고 생각할 수 있다. 이에 본 논문은 linear 예측을 잘하는 GMF, non-linear 예측을 잘 하는 MLP 두가지를 섞어서 모델을 제안한다. 구조는 아래의 Figure 3과 같다.

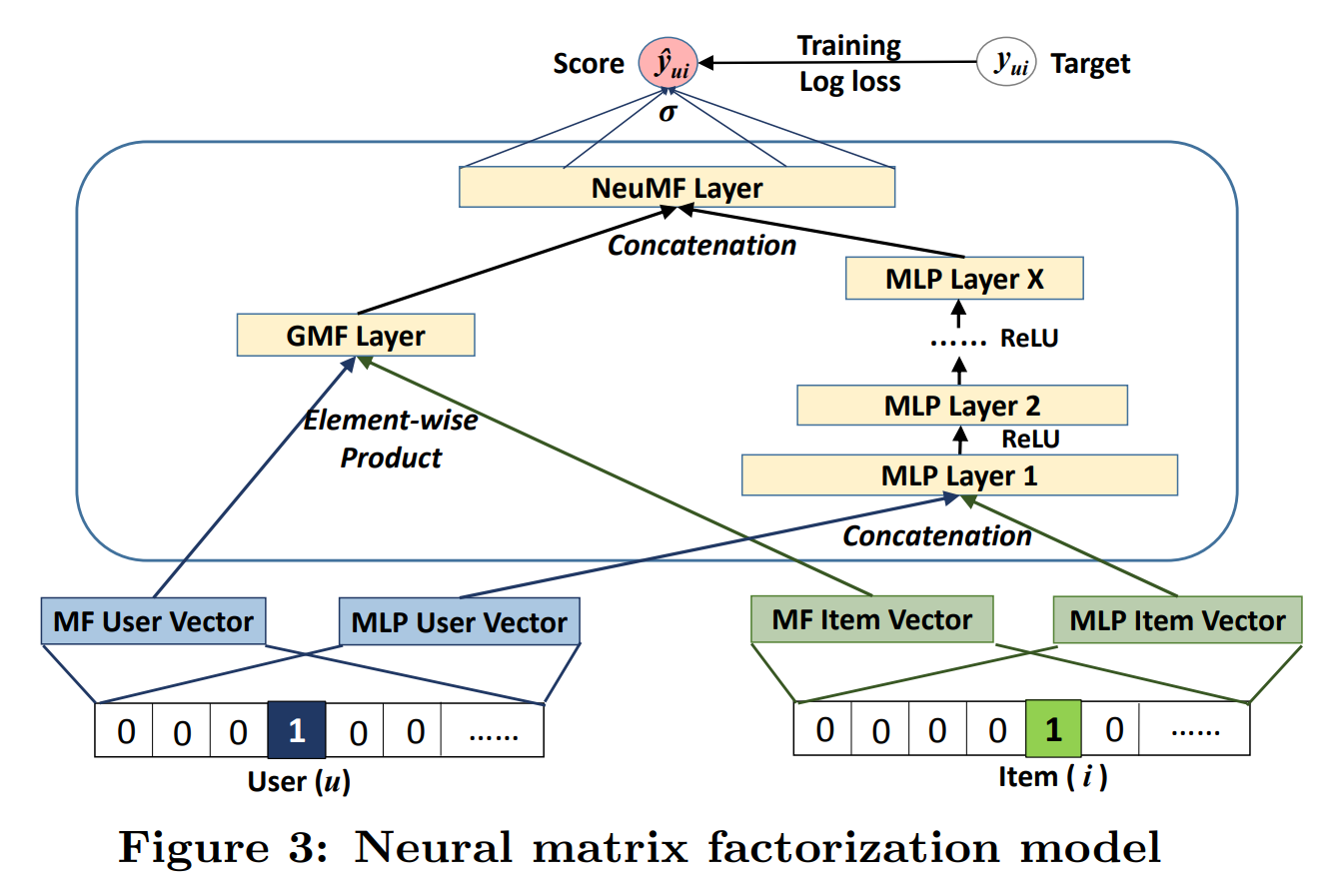
가장 핵심은, GMF와 MLP에 대해서 embedding vector를 따로 생성한다는 점이다. 두가지 다른 구조에 대해서, 다른 차원의 embedding이 가능하다. 또한 논문은 Neural network를 내적 대신 사용하는것에 주안점을 두어 따로 더 진행하지는 않았지만, Figure 3을 보면 Factorization Machine (FM)과 같이 context 정보를 활용할 수 있다는 것을 알 수 있다.

이렇게 두 구조를 합친 최종 모델을 제시했고, 이름은 NeuMF, Neural Matrix Factorization이라 하였다.

3.4.1 Pre-training

Gradient descent method를 사용 할 때, 찾아낸 최솟값이 global minimum임을 보장할 수 없다. 따라서 Gradient descent method를 사용 할 경우, 학습 parameter 초기화가 성능에 영향을 미친다. 본 논문에서는 NeuMF의 parameter를 초기화하는 방법으로 GMF와 MLP에 대해 각각 학습을 진행하고, 학습의 결과를 이용하여 NeuMF의 파라미터를 초기화 할 것을 추천했다.

다만 여기서 주의할 사항이 있다. 바로 흔히 optimizer로 활용되는 Adam을 사용하는 경우이다. GMF와 MLP를 각각 학습할 때에는 문제가 되지 않는다. 다만 이 학습된 GMF와 MLP를 NeuMF에 적용 후, 학습을 시작할 때에는 문제가 된다. 이름에서 알 수 있듯, Adam은 momentum을 활용하는데, 이전의 momentum에 대한 정보가 없기 때문에, 부정확한 결과를 낳을 수 있다. 따라서 본 논문에서는 pre-train(GMF, MLP)을 할 때에만 Adam을 사용하고, 이후에는 vanilla SGD를 사용했다고 언급한다.