[딥러닝] Batch Normalization

zzwon1212·2024년 1월 2일

딥러닝

목록 보기

12/33

1. Normalizing Activations in a Network

개념
Batch Normalization은 한 mini-batch에서 각 층의 각 unit별 Convolution 결과( $z$ )를 평균이 $\mu$ , 표준편차가 $\gamma$ 인 정규분포로 변환한다. (scale과 shift 미적용 시 평균이 0, 표준편차가 1인 표준정규분포)
Batch Norm과 활성화 함수의 순서
활성화 함수 이전 값( $z$ )을 Norm할 것인지, 활성화 함수 이후 값( $a$ )을 Norm할 것인지 둘 사이에 논쟁이 있었다. 현재는 활성화 함수 이전에 Batch Norm을 적용하는 것이 더 효과적이라 여겨진다. 활성화 함수 이후에 Batch Norm을 적용하면 활성화 함수의 비선형 특성이 깨질 우려가 있기 때문이다. 활성화 함수 이후에 Norm을 하는 것은 학습 과정에 불안정성을 초래할 수 있다.

scale( $\gamma$ )과 shift( $\beta$ )
$L: layers, \, m: batch \, size, \, n^{[l]}: hidden \, units \\ \, \\ z^{(i)} = z_j^{[l](i)}, \, (l = 1, \cdots, L), \, (i = 1, \cdots, m), \, (j = 1, \cdots, n^{[l]}) \\ \, \\ \mu = {1 \over m} \sum_i^m z^{(i)} \\ \, \\ \sigma^2 = {1 \over m} \sum_i^m (z^{(i)} - \mu)^2 \\ \, \\ z_{norm}^{(i)} = {z^{(i)} - \mu \over \sqrt{\sigma^2 + \epsilon}} \\ \, \\ \tilde{z}^{(i)} = \gamma z_{norm}^{(i)} + \beta \\$
- $\gamma$ 와 $\beta$ 는 learnable parameters이다.
- 적용하는 이유 [Andrew Ng]
  각 mini-batch의 각 층의 $z$ 값들이 다양한 분포를 가지도록 하여 모델이 데이터의 분포를 자유롭게 학습하도록 하기 위함이다. 각 층의 $z$ 값들을 하나의 표준정규분포를 가지도록 강제하면 모델의 표현력이 제한될 수 있기 때문이다.

2. Fitting Batch Norm into Neural Networks

Update $\gamma$ and $\beta$

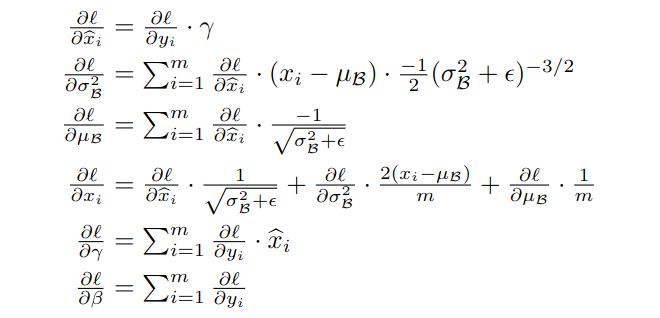
3. Why does Batch Norm Work?

3.1. 학습 속도 향상

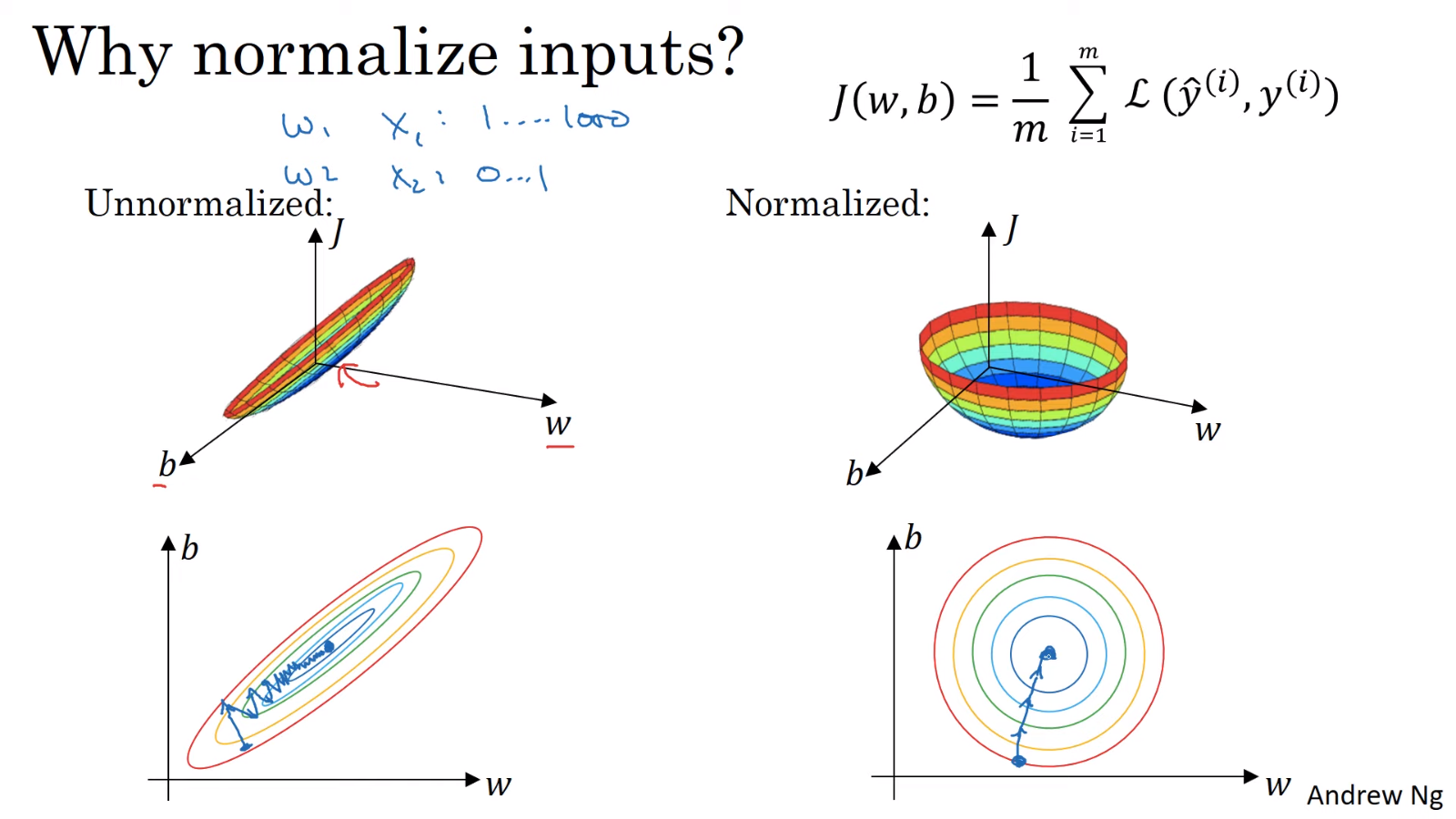
3.2. Reducing Internal Covariance Shift

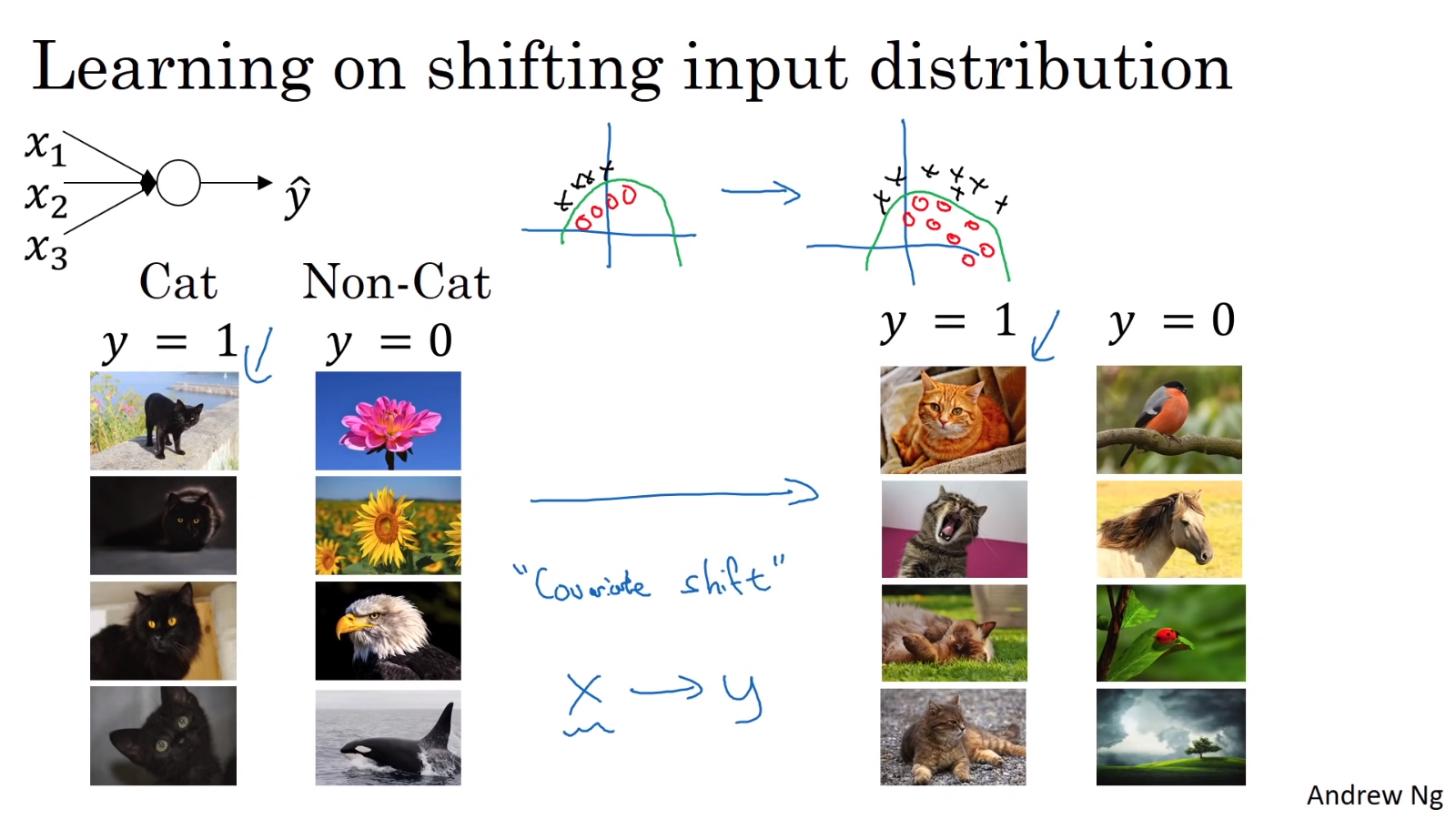
위 사진처럼 X의 분포가 바뀌면(covariance shift가 발생하면) 다시 학습해야 한다.

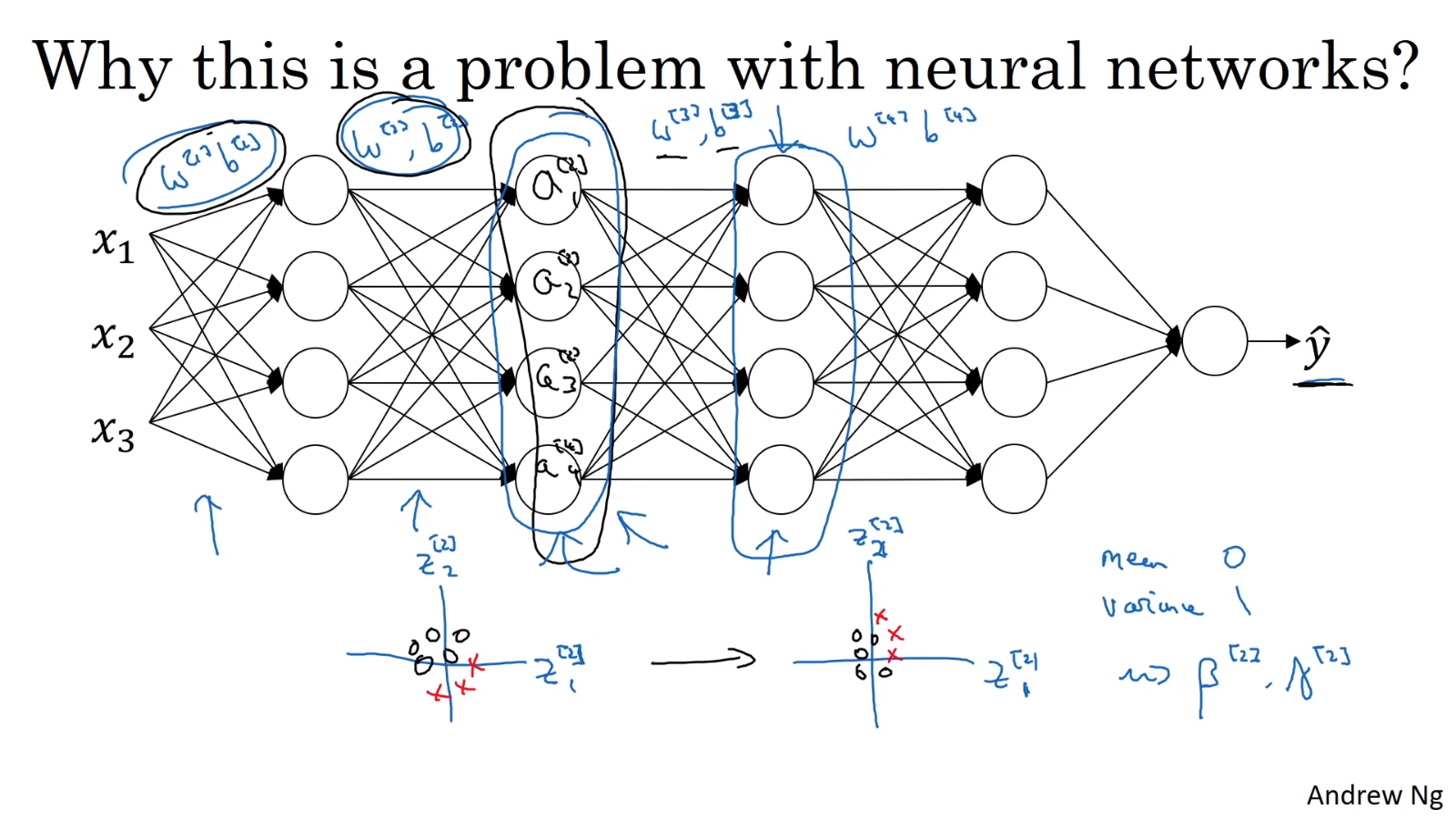
마찬가지로 신경망도 학습을 거듭하며 얕은 층의 가중치가 update되고 activation 값도 변하게 되는데, 이는 깊은 층의 가중치 입장에서 Internal Covariance Shift가 발생하는 것이다. 이때 batch norm을 적용하면 얕은 층의 값들의 변화를 줄여주기 때문에(평균과 분산을 일정하게 유지하기 때문에), 깊은 층의 가중치가 얕은 층의 가중치 변화에 robust하게 되고 학습을 안정화시킬 수 있다.

3.3. as Regularization

각 mini-batch로 평균과 분산을 구하여 normalize하기 때문에 전체 데이터로 normalize하는 것에 비해 각 층의 activation에 일종의 노이즈를 추가하는 것이 된다. 이는 dropout과 유사한 (아주 약간의) regularization 효과이다. mini-batch 크기가 커지면 regularization의 효과가 줄어드는 것은 batch norm의 이상한 특징이다. batch norm은 regularization을 목적으로 만들어진 것은 아니기 때문에 Andrew Ng은 regularization을 목적으로 batch norm을 사용하지는 않는다.

4. Batch Norm at Test Time

test time에는 한 sample만을 이용하기 때문에 batch norm을 적용하기 위한 평균과 분산을 구할 수 없다. 따라서 test time에 사용할 평균과 분산을 train time에 미리 구해두어야 한다. 전체 데이터에 대한 평균과 분산을 한 번에 구하는 것은, 모든 훈련 데이터를 사용해야 하므로 많은 메모리와 계산량이 필요하다. 따라서 mini-batch마다 구했던 $\mu$ 와 $\sigma$ 의 exponential moving average를 전체 데이터에 대한 평균과 분산의 추정치로써 이용한다.