[딥러닝] Backpropagation in CNN

zzwon1212·2023년 12월 22일
딥러닝
0

딥러닝

목록 보기
7/33
post-thumbnail

# 2에서 CNN의 backpropagation을 공부하기 전에 먼저 #1에서 Logistic regression의 backpropagtaion을 살펴보자.

1. Logistic Regression

  • (위 그림과 같은 연산 그래프를 적극 활용하기)

  • Logistic regression의 backpropagation을 살펴보자.

  • Sigmoid function과, Logistic regression의 cost function은 [Sigmoid function, Cost function of Logistic regression]를 참고.

  • 경사 하강법(Gradient Descent)
    cost를 최소화하기 위해 매 단계마다 ∂L∂w{\partial{L} \over \partial{w}}과 ∂L∂b{\partial{L} \over \partial{b}}를 구하여 ww와 bb를 업데이트해야 한다.
    (미니 배치 기반의 확률론적 경사 하강법이 표준으로 여겨지고 있다.)

  • Vanishing gradient를 주의하자.

1.1. Forward propagation

① w,bw, b
↓
② z=wx+bz = wx + b
↓
③ y^=a=σ(z)\hat{y} = a = \sigma(z)
↓
④ L(a,y)=−(ylog⁡a+(1−y)log⁡(1−a))L(a, y) = -(y \log{a} + (1-y) \log{(1-a)})

1.2. Computing gradients

  • gradients

    • ∂L∂w=∂L∂a∂a∂z∂z∂w{\partial{L} \over \partial{w}} = {\partial{L} \over \partial{a}} {\partial{a} \over \partial{z}} {\partial{z} \over \partial{w}}

    • ∂L∂b=∂L∂a∂a∂z∂z∂b{\partial{L} \over \partial{b}} = {\partial{L} \over \partial{a}} {\partial{a} \over \partial{z}} {\partial{z} \over \partial{b}}

  • chain rule을 활용하여 아래 미분식을 천천히 계산해보자.

④ ∂L∂a=−ya+1−y1−a{\partial{L} \over \partial{a}} = -{y \over a} + {1-y \over 1-a}
↓
③ ∂a∂z=a(1−a){\partial{a} \over \partial{z}} = a(1-a)
↓
② ∂z∂w=x{\partial{z} \over \partial{w}} = x
↓
① ∂L∂w=∂L∂a∂a∂z∂z∂w=(−ya+1−y1−a)a(1−a)x=(a−y)XT{\partial{L} \over \partial{w}} = {\partial{L} \over \partial{a}} {\partial{a} \over \partial{z}} {\partial{z} \over \partial{w}} = (-{y \over a} + {1-y \over 1-a}) a(1-a) x = (a-y)X^T

① ∂L∂b=(a−y)⋅1{\partial{L} \over \partial{b}} = (a-y)\cdot1

1.3. updating weights

위에서 구한 gradients를 이용해 매 단계마다 아래와 같이 ww와 bb를 업데이트해준다. 여기서 α\alpha는 hyperparameter 중 하나인 learning rate이다.

  • w=w−α∂L∂w=w−α(a−y)XTw = w - \alpha {\partial{L} \over \partial{w}} = w - \alpha (a-y) X^T
  • b=b−α∂L∂b=b−α(a−y)⋅1b = b - \alpha {\partial{L} \over \partial{b}} = b - \alpha (a-y) \cdot 1

1.4. 도함수의 종류

2. CNN

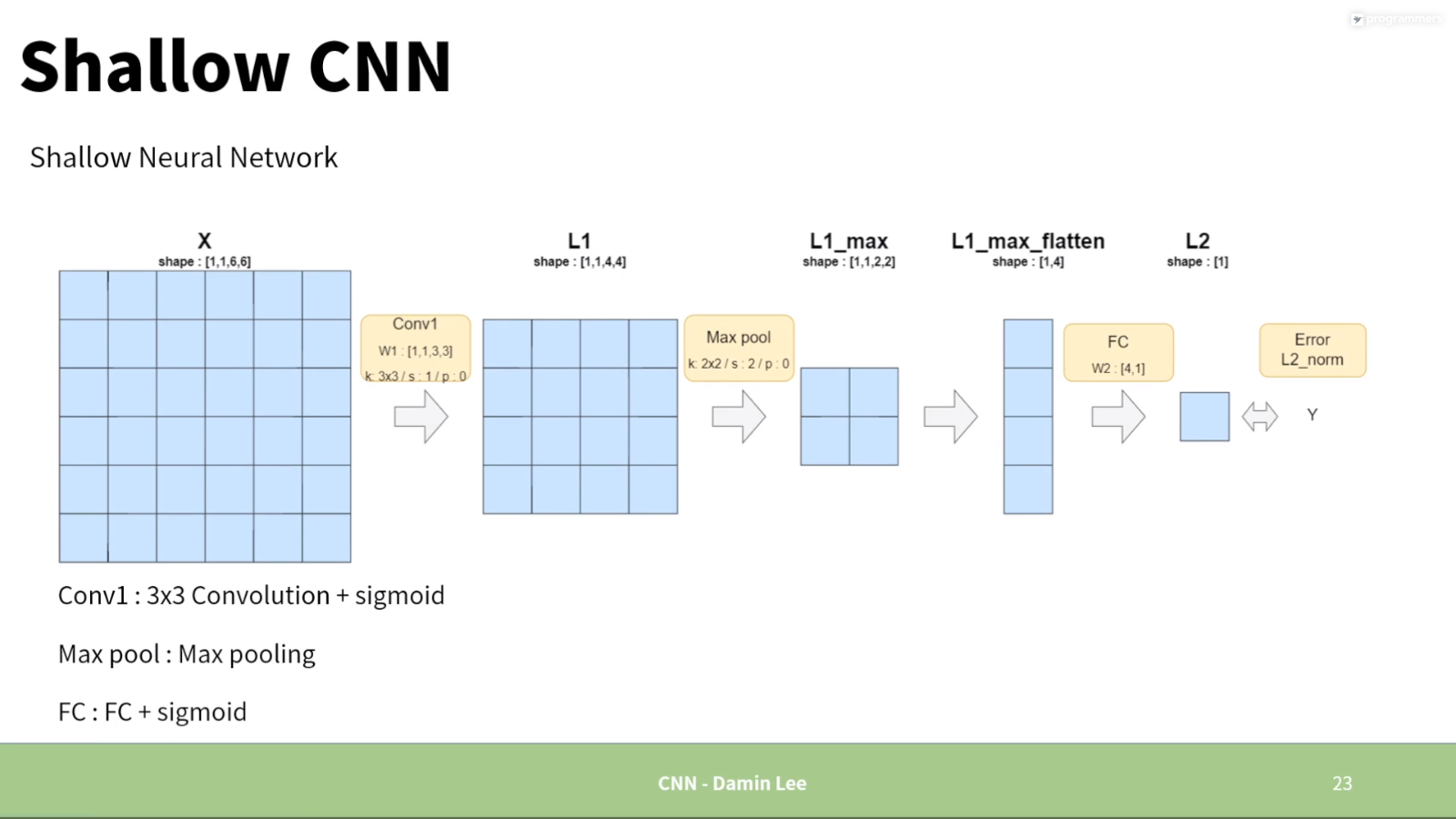
2.1. 그림으로 이해하기

2.1.1. Forward

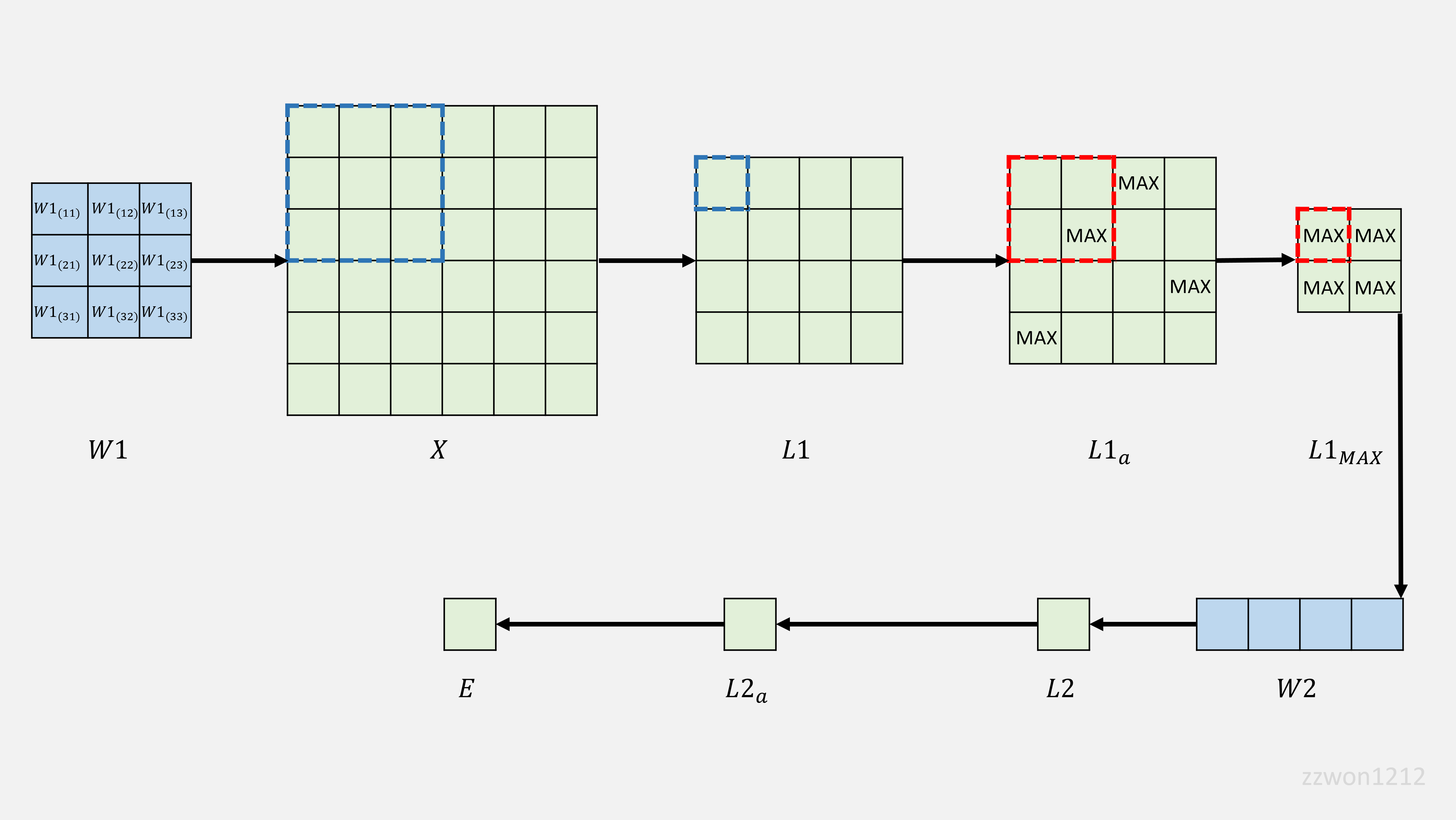
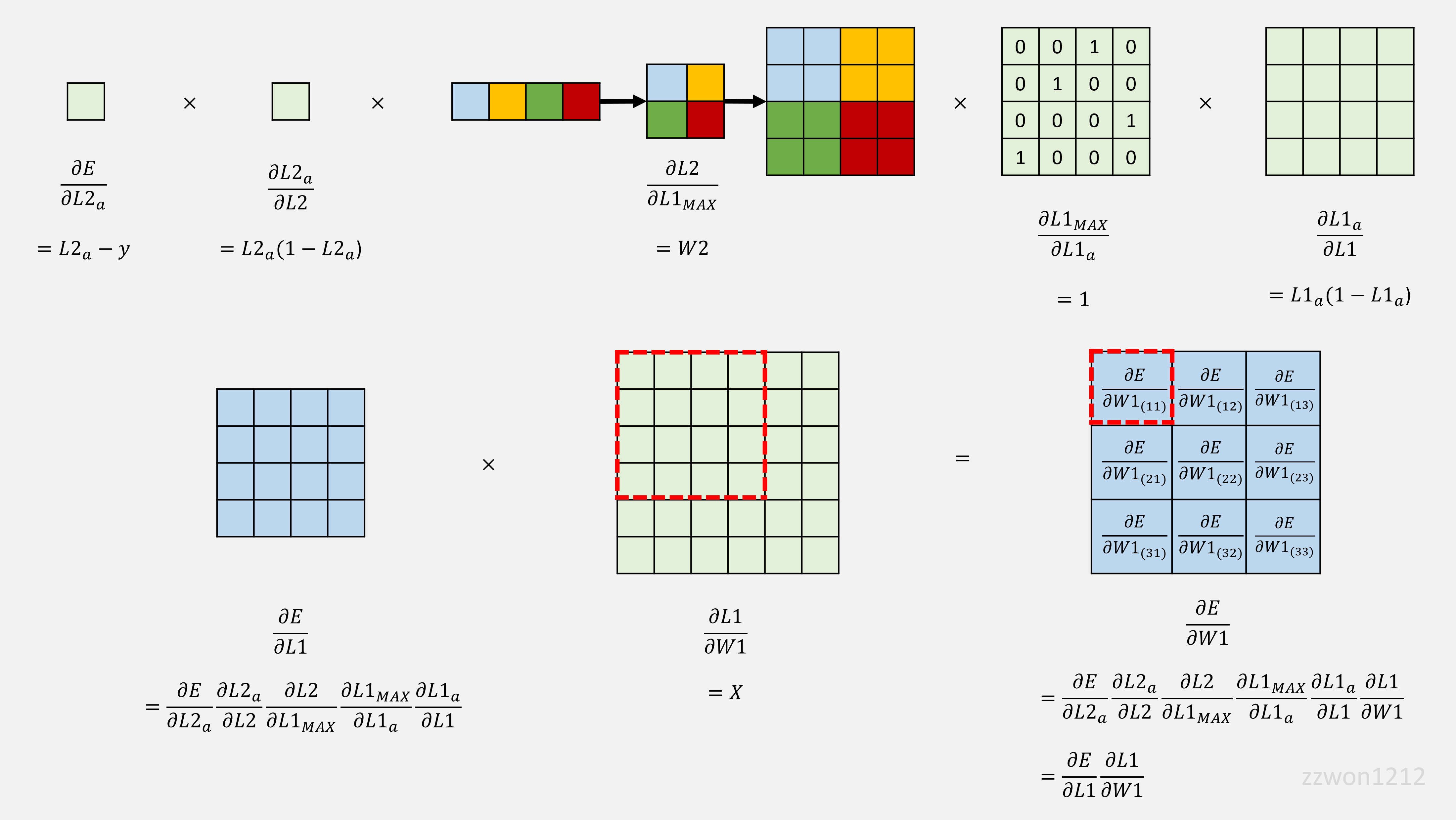
2.1.2. W1의 backpropagation

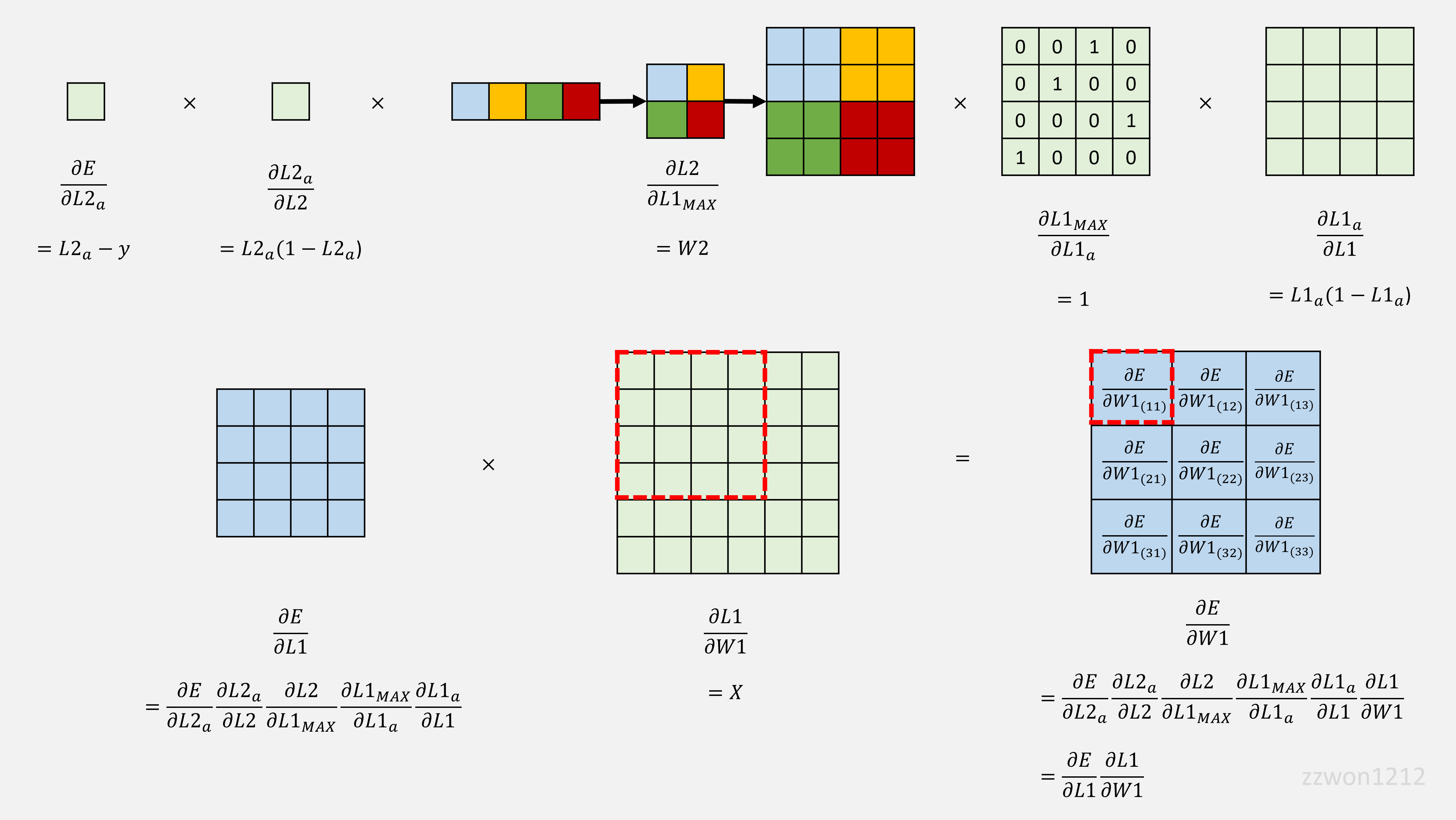
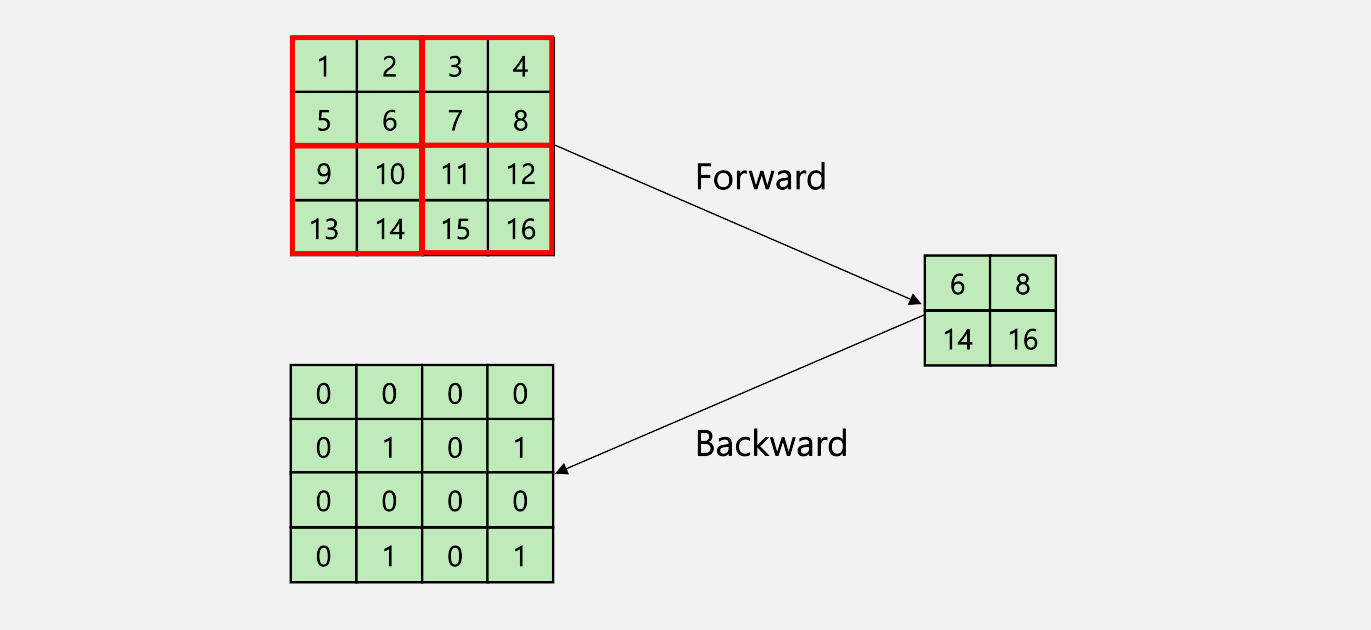
2.1.3. Max Pooling의 backpropagation

2.2. Forward propagation

① w1,w2w_1, w_2
↓
② L1=w1xL1 = w_1 x
↓
③ L1a=σ(L1)L1_a = \sigma(L1)
↓
④ L1max=Poolmax(L1a)L1_{max} = Pool_{max}(L1_a)
↓
⑤ L2=w2L1maxL2 = w_2 L1_{max}
↓
⑥ L2a=σ(L2)L2_a = \sigma(L2)
↓
⑦ E=12(y−L2a)2E = {1 \over 2}(y-L2_a)^2

2.3. Computing gradients

2.3.1. ∂E∂w2=∂E∂L2a∂L2a∂L2∂L2∂w2{\partial{E} \over \partial{w_2}} = {\partial{E} \over \partial{L2_a}} {\partial{L2_a} \over \partial{L2}} {\partial{L2} \over \partial{w_2}}

⑦ ∂E∂L2a=L2a−y{\partial{E} \over \partial{L2_a}} = L2_a - y
↓
⑥ ∂L2a∂L2=L2a(1−L2a){\partial{L2_a} \over \partial{L2}} = L2_a(1 - L2_a)
↓
⑤ ∂L2∂w2=L1max{\partial{L2} \over \partial{w_2}} = L1_{max}
↓
① ∂E∂w2=∂E∂L2a∂L2a∂L2∂L2∂w2=(L2a−y)⋅L2a(1−L2a)⋅L1max{\partial{E} \over \partial{w_2}} = {\partial{E} \over \partial{L2_a}} {\partial{L2_a} \over \partial{L2}} {\partial{L2} \over \partial{w_2}} = (L2_a - y) \cdot L2_a(1 - L2_a) \cdot L1_{max}

2.3.2. ∂E∂w1=∂E∂L2a∂L2a∂L2∂L2∂L1max∂L1max∂L1a∂L1a∂L1∂L1∂w1{\partial{E} \over \partial{w_1}} = {\partial{E} \over \partial{L2_a}} {\partial{L2_a} \over \partial{L2}} {\partial{L2} \over \partial{L1_{max}}} {\partial{L1_{max}} \over \partial{L1_a}} {\partial{L1_a} \over \partial{L1}} {\partial{L1} \over \partial{w_1}}

⑦⑥ ∂E∂L2a∂L2a∂L2=(L2a−y)⋅L2a(1−L2a){\partial{E} \over \partial{L2_a}} {\partial{L2_a} \over \partial{L2}} = (L2_a - y) \cdot L2_a(1 - L2_a)
↓
⑤ ∂L2∂L1max=w2{\partial{L2} \over \partial{L1_{max}}} = w_2
↓
④ ∂L1max∂L1a=1{\partial{L1_{max}} \over \partial{L1_a}} = 1
↓
③ ∂L1a∂L1=L1a(1−L1a){\partial{L1_a} \over \partial{L1}} = L1_a(1 - L1_a)
↓
② ∂L1∂w1=x{\partial{L1} \over \partial{w_1}} = x
↓
① ∂E∂w1=∂E∂L2a∂L2a∂L2∂L2∂L1max∂L1max∂L1a∂L1a∂L1∂L1∂w1=(L2a−y)⋅L2a(1−L2a)⋅w2⋅1⋅L1a(1−L1a)⋅x{\partial{E} \over \partial{w_1}} = {\partial{E} \over \partial{L2_a}} {\partial{L2_a} \over \partial{L2}} {\partial{L2} \over \partial{L1_{max}}} {\partial{L1_{max}} \over \partial{L1_a}} {\partial{L1_a} \over \partial{L1}} {\partial{L1} \over \partial{w_1}} = (L2_a - y) \cdot L2_a(1 - L2_a) \cdot w_2 \cdot 1 \cdot L1_a(1 - L1_a) \cdot x

2.4. updating weights

위에서 구한 gradients를 이용해 매 단계마다 아래와 같이 w1w_1와 w2w_2를 업데이트해준다. α\alpha는 learning rate이다.

  • w2=w2−α∂E∂w2=w2−α⋅(L2a−y)⋅L2a(1−L2a)⋅L1maxw_2 = w_2 - \alpha {\partial{E} \over \partial{w_2}} = w_2 - \alpha \cdot (L2_a - y) \cdot L2_a(1 - L2_a) \cdot L1_{max}
  • w1=w1−α∂E∂w1=w1−α⋅(L2a−y)⋅L2a(1−L2a)⋅w2⋅1⋅L1a(1−L1a)⋅xw_1 = w_1 - \alpha {\partial{E} \over \partial{w_1}} = w_1 - \alpha \cdot (L2_a - y) \cdot L2_a(1 - L2_a) \cdot w_2 \cdot 1 \cdot L1_a(1 - L1_a) \cdot x

2.5. Code

2.5.1. NumPy

2.5.2. PyTorch

w1w1의 backpropagation

  • 코드

    import numpy as np
import torch
import torch.nn.functional as F

X = torch.arange(1, 37, dtype=torch.float32).view(1, 1, 6, 6)
print(f"X\n{X}, {X.shape}")
W1 = torch.tensor([[0.01, 0, 0], [0, 0.01, 0], [0, 0, 0.01]], dtype=torch.float32).view(1, 1, 3, 3)
print(f"W1\n{W1}, {W1.shape}")
W2 = torch.tensor([0, 0.01, 0, 0.01], dtype=torch.float32).view(1, 4)
print(f"W2\n{W2}, {W2.shape}")
Y = torch.tensor([1], dtype=torch.float32).view(1, 1)
print(f"Y\n{Y}, {Y.shape}")

# Forward
print("\n@@@@@@@@@@@@@@ Forward @@@@@@@@@@@@@@\n")
L1 = F.conv2d(input=X, weight=W1)
print(f"L1\n{L1}, {L1.shape}")

L1_a = F.sigmoid(L1)
print(f"L1_a\n{L1_a}, {L1_a.shape}")

L1_MAX = F.max_pool2d(input=L1_a, kernel_size=2, stride=2, padding=0)
print(f"L1_MAX\n{L1_MAX}, {L1_MAX.shape}")
L1_MAX_flatten = L1_MAX.view(1, -1)
print(f"L1_MAX_flatten\n{L1_MAX_flatten}, {L1_MAX_flatten.shape}")

L2 = F.linear(input=L1_MAX_flatten, weight=W2)
print(f"L2\n{L2}, {L2.shape}")

L2_a = F.sigmoid(L2)
print(f"L2_a\n{L2_a}, {L2_a.shape}")

E = np.square(Y - L2_a) * 0.5
print(f"E\n{E}, {E.shape}")

# Backward
print("\n@@@@@@@@@@@@@@ Backward @@@@@@@@@@@@@@\n")
dE = L2_a - Y
print(f"dE\n{dE}, {dE.shape}")

dL2_a = L2_a * (1 - L2_a)
print(f"dL2_a\n{dL2_a}, {dL2_a.shape}")

dL2 = W2.view(2, 2).repeat_interleave(2, dim=0).repeat_interleave(2, dim=1)
print(f"dL2\n{dL2}, {dL2.shape}")

dL1_MAX = L1_MAX.repeat_interleave(2, dim=2).repeat_interleave(2, dim=3)
dL1_MAX = torch.eq(dL1_MAX, L1_a)
print(L1_a)
print(f"dL1_MAX\n{dL1_MAX}, {dL1_MAX.shape}")

dL1_a = L1_a * (1 - L1_a)
print(f"dL1_a\n{dL1_a}, {dL1_a.shape}")

dL1 = X
print(f"dL1\n{dL1}, {dL1.shape}")

dE__dL1 = dE * dL2_a * dL2 * dL1_MAX * dL1_a
print(f"dE__dL1\n{dE__dL1}, {dE__dL1.shape}")

diff = F.conv2d(input=X, weight=dE__dL1)
print(f"diff\n{diff}, {diff.shape}")

# Update weights
print("\n@@@@@@@@@@@@@@ Update weights @@@@@@@@@@@@@@\n")
print(f"W1\n{W1}")
W1 = W1 - 1 * diff
print(f"Updated W1\n{W1}")

  • 결과

    X
tensor([[[[ 1.,  2.,  3.,  4.,  5.,  6.],
          [ 7.,  8.,  9., 10., 11., 12.],
          [13., 14., 15., 16., 17., 18.],
          [19., 20., 21., 22., 23., 24.],
          [25., 26., 27., 28., 29., 30.],
          [31., 32., 33., 34., 35., 36.]]]]), torch.Size([1, 1, 6, 6])
W1
tensor([[[[0.0100, 0.0000, 0.0000],
          [0.0000, 0.0100, 0.0000],
          [0.0000, 0.0000, 0.0100]]]]), torch.Size([1, 1, 3, 3])
W2
tensor([[0.0000, 0.0100, 0.0000, 0.0100]]), torch.Size([1, 4])
Y
tensor([[1.]]), torch.Size([1, 1])

@@@@@@@@@@@@@@ Forward @@@@@@@@@@@@@@

L1
tensor([[[[0.2400, 0.2700, 0.3000, 0.3300],
          [0.4200, 0.4500, 0.4800, 0.5100],
          [0.6000, 0.6300, 0.6600, 0.6900],
          [0.7800, 0.8100, 0.8400, 0.8700]]]]), torch.Size([1, 1, 4, 4])
L1_a
tensor([[[[0.5597, 0.5671, 0.5744, 0.5818],
          [0.6035, 0.6106, 0.6177, 0.6248],
          [0.6457, 0.6525, 0.6593, 0.6660],
          [0.6857, 0.6921, 0.6985, 0.7047]]]]), torch.Size([1, 1, 4, 4])
L1_MAX
tensor([[[[0.6106, 0.6248],
          [0.6921, 0.7047]]]]), torch.Size([1, 1, 2, 2])
L1_MAX_flatten
tensor([[0.6106, 0.6248, 0.6921, 0.7047]]), torch.Size([1, 4])
L2
tensor([[0.0133]]), torch.Size([1, 1])
L2_a
tensor([[0.5033]]), torch.Size([1, 1])
E
tensor([[0.1233]]), torch.Size([1, 1])

@@@@@@@@@@@@@@ Backward @@@@@@@@@@@@@@

dE
tensor([[-0.4967]]), torch.Size([1, 1])
dL2_a
tensor([[0.2500]]), torch.Size([1, 1])
dL2
tensor([[0.0000, 0.0000, 0.0100, 0.0100],
        [0.0000, 0.0000, 0.0100, 0.0100],
        [0.0000, 0.0000, 0.0100, 0.0100],
        [0.0000, 0.0000, 0.0100, 0.0100]]), torch.Size([4, 4])
tensor([[[[0.5597, 0.5671, 0.5744, 0.5818],
          [0.6035, 0.6106, 0.6177, 0.6248],
          [0.6457, 0.6525, 0.6593, 0.6660],
          [0.6857, 0.6921, 0.6985, 0.7047]]]])
dL1_MAX
tensor([[[[False, False, False, False],
          [False,  True, False,  True],
          [False, False, False, False],
          [False,  True, False,  True]]]]), torch.Size([1, 1, 4, 4])
dL1_a
tensor([[[[0.2464, 0.2455, 0.2445, 0.2433],
          [0.2393, 0.2378, 0.2361, 0.2344],
          [0.2288, 0.2267, 0.2246, 0.2225],
          [0.2155, 0.2131, 0.2106, 0.2081]]]]), torch.Size([1, 1, 4, 4])
dL1
tensor([[[[ 1.,  2.,  3.,  4.,  5.,  6.],
          [ 7.,  8.,  9., 10., 11., 12.],
          [13., 14., 15., 16., 17., 18.],
          [19., 20., 21., 22., 23., 24.],
          [25., 26., 27., 28., 29., 30.],
          [31., 32., 33., 34., 35., 36.]]]]), torch.Size([1, 1, 6, 6])
dE__dL1
tensor([[[[-0.0000, -0.0000, -0.0000, -0.0000],
          [-0.0000, -0.0000, -0.0000, -0.0003],
          [-0.0000, -0.0000, -0.0000, -0.0000],
          [-0.0000, -0.0000, -0.0000, -0.0003]]]]), torch.Size([1, 1, 4, 4])
diff
tensor([[[[-0.0086, -0.0091, -0.0097],
          [-0.0119, -0.0124, -0.0130],
          [-0.0152, -0.0157, -0.0163]]]]), torch.Size([1, 1, 3, 3])

@@@@@@@@@@@@@@ Update weights @@@@@@@@@@@@@@

W1
tensor([[[[0.0100, 0.0000, 0.0000],
          [0.0000, 0.0100, 0.0000],
          [0.0000, 0.0000, 0.0100]]]])
Updated W1
tensor([[[[0.0186, 0.0091, 0.0097],
          [0.0119, 0.0224, 0.0130],
          [0.0152, 0.0157, 0.0263]]]])

  • Error 비교
    update 후 Error가 줄었다.

    • 최초 Error
      E
tensor([[0.1233]]), torch.Size([1, 1])
    • w1w1을 한 번 update한 후 Error (learning rate=1)
      E
tensor([[0.1226]]), torch.Size([1, 1])

📙 참고

profile
zzwon1212
JUST DO IT.
이전 포스트

[딥러닝] Activation, Pooling, Fully Connected layers 구현

다음 포스트

[딥러닝] Optimizer

0개의 댓글

관련 채용 정보