1. Sigmoid function
- 아래 항목들을 따라가며 sigomid function을 유도해보자.
1.1. 정의
-
binary 사건 Y의 발생 확률
-
오즈(odds): 성공 확률과 실패 확률의 비율
-
로짓(logit): odds의 로그 변환
- 0에서 1까지의 확률을 실수 전체의 범위로 변환하는 역할
1.2. Logistic regression
-
위의 logit에 선형 회귀 모형을 적용한 것을 Logistic regression이라고 한다.
-
여기서는 독립변수 가 1개인 simple logistic regression으로 식을 전개해보자.
1.3. Sigmoid function과 그래프
위의 수식 전개를 통해 구한 p에서 로 치환하면 sigmoid function을 아래와 같이 나타낼 수 있다.
- Sigmoid function
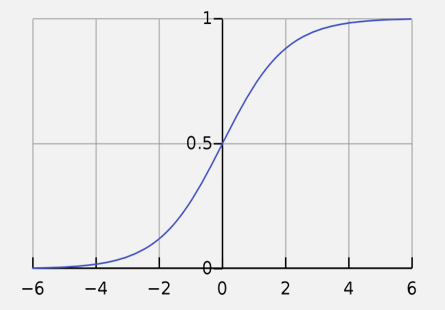
- If is large,
- If is large negative,
2. Logistic regression의 Cost function
- Logistic regression
- , where
2.1. Loss function
-
-
If ,
이 0에 가까우면 loss값이 커지고, 이 1에 가까우면 loss값이 0으로 수렴한다. -
If ,
이 0에 가까우면 loss값이 0으로 수렴하고, 이 1에 가까우면 loss값이 커진다.
즉, 예측값 들이 실제값 들을 잘 맞힌다면 아래 정의한 cost가 작아지고, 많이 틀린다면 cost가 커진다.
-