Geometric Processing

hunnypooh·2022년 10월 21일

opencv

디지털 영상 처리(OpenCV)

목록 보기

5/7

Forward Mapping VS Backward Mapping

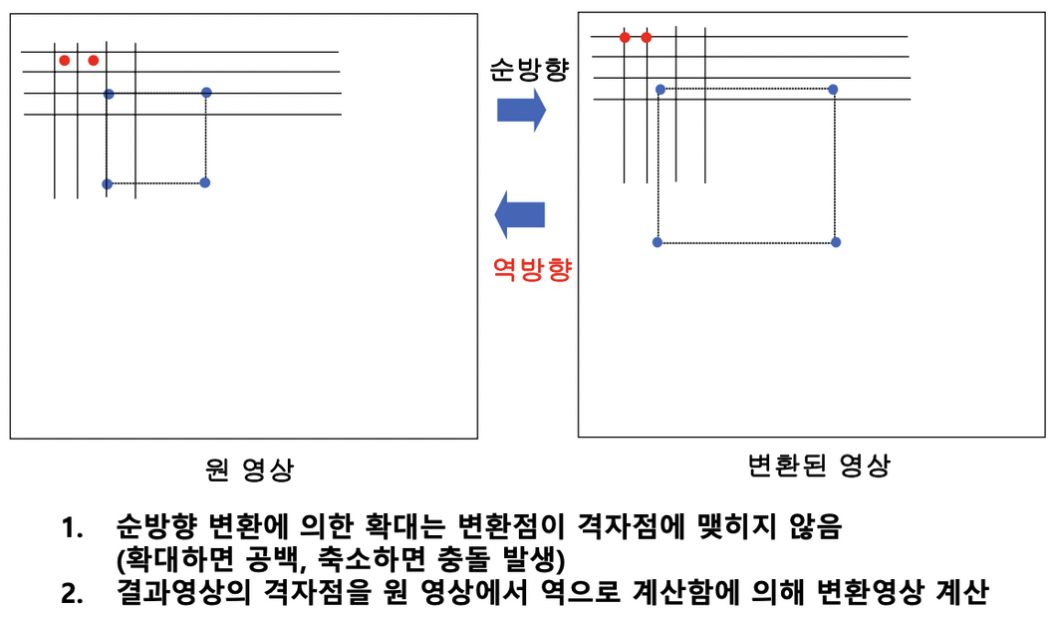
순방향 매핑 (forward mapping) (원본 → 목적)
- 원본 이미지의 픽셀을 하나씩 목적 이미지으로 이동시킴
- 이미지상에서 공백이나 충돌이 발생
- $I_{output} = f (I_{input})$
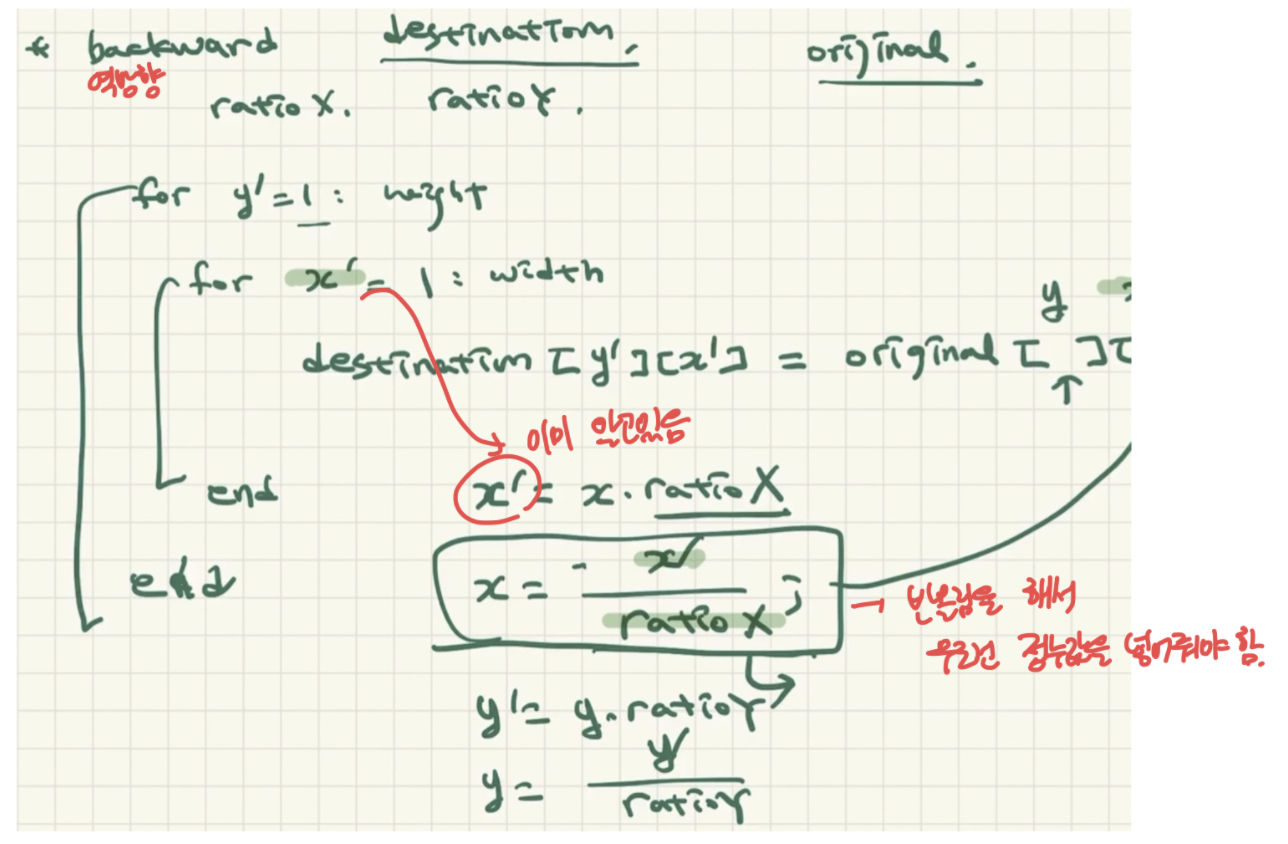
역방향 매핑 (backward mapping) (목적 ← 원본)
- 목적이미지에서 채울 값을 원본 이미지에서 가져옴.
- $f^{-1}(I_{output}) = I _{input}$ 시
- 실제 구현에서 역방향 매핑을 많이 사용!

영상의 확대 축소

역방향 매핑 사용
실수 배의 영상 확대도 가능
확대 - 목적 이미지의 크기를 배율에 의해 계산 후 그 지점에서 밝기 값 가져옴.
축소 - 목적 이미지에서 밝기 값을 선택할 때 간단하게 원 이미지상의 한 점에서 밝기 값 이용해서 대표 밝기를 구함

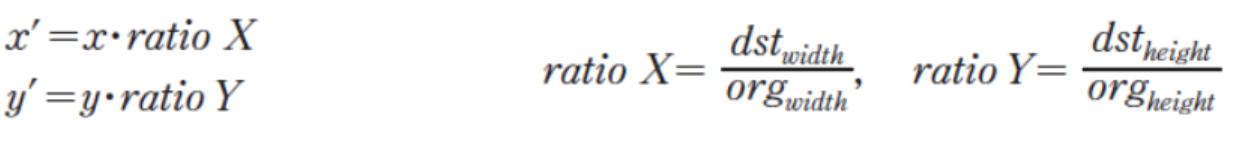
x’ : 목적 x좌표
x : 원래 x좌표
ratio는 독립적이라서 각각 다른 비율로 할 수 있음
- ex) ratioX = 2, ratioY = 0.5

영상의 보간 (Interpolation)

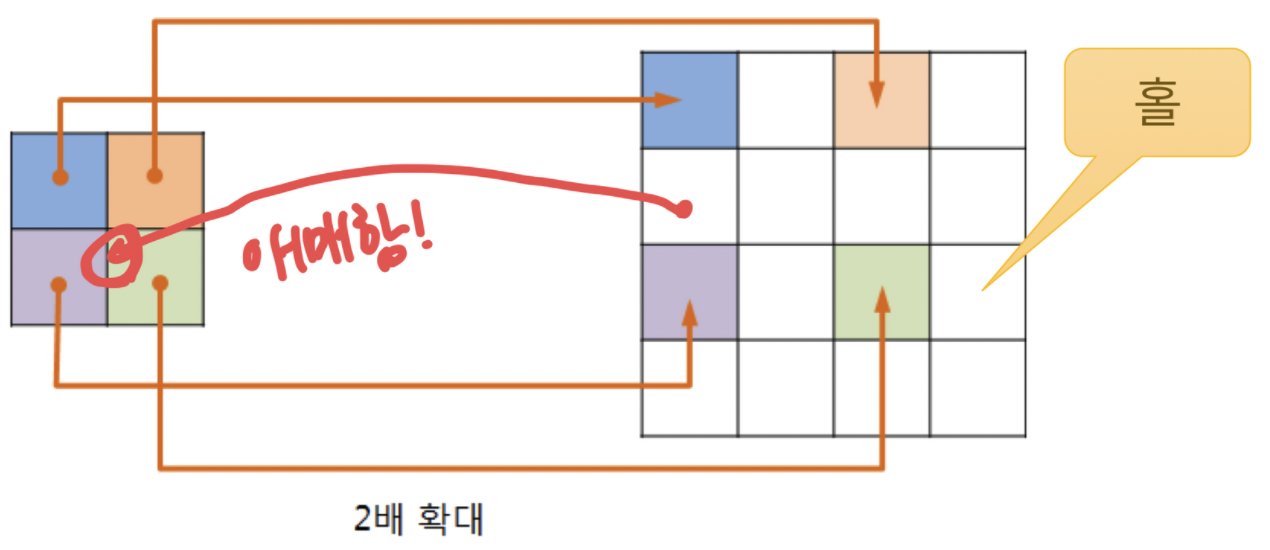
역방향 사상을 통해서 홀의 화소들을 입력 영상에서 찾음
목적영상에서 홀의 화소들을 채우고(확대), 오버랩 되지 않게(축소) 화소들을 배치해서 목적영상을 만드는 기법

최근접 이웃 보간법 (NN)

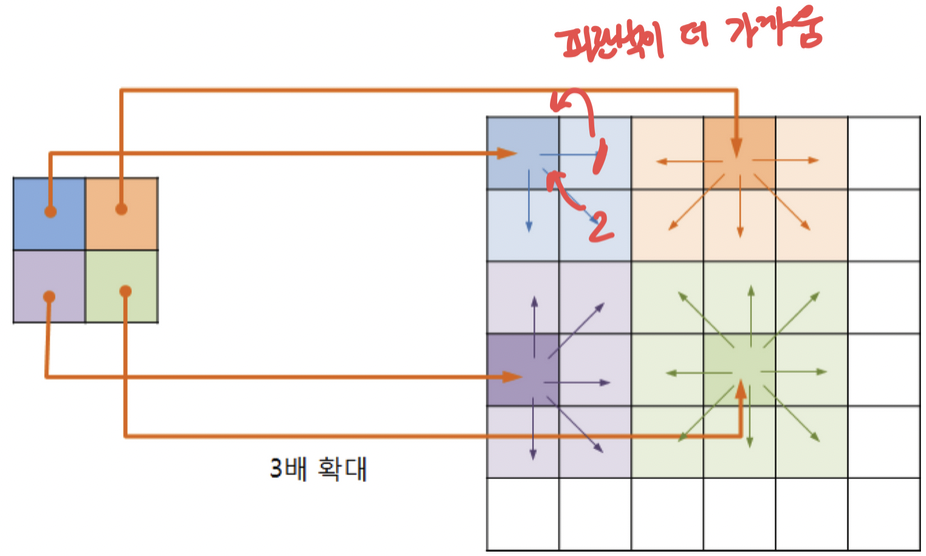
목적영상의 화소에 가장 가깝게 이웃한 입력영상의 화소값을 가져오는 방법
단점 : 확대 비율이 커지면, 모자이크 현상 또는 경계부분에서 계단현상 발생 (화질 나쁨)

양선형 보간법

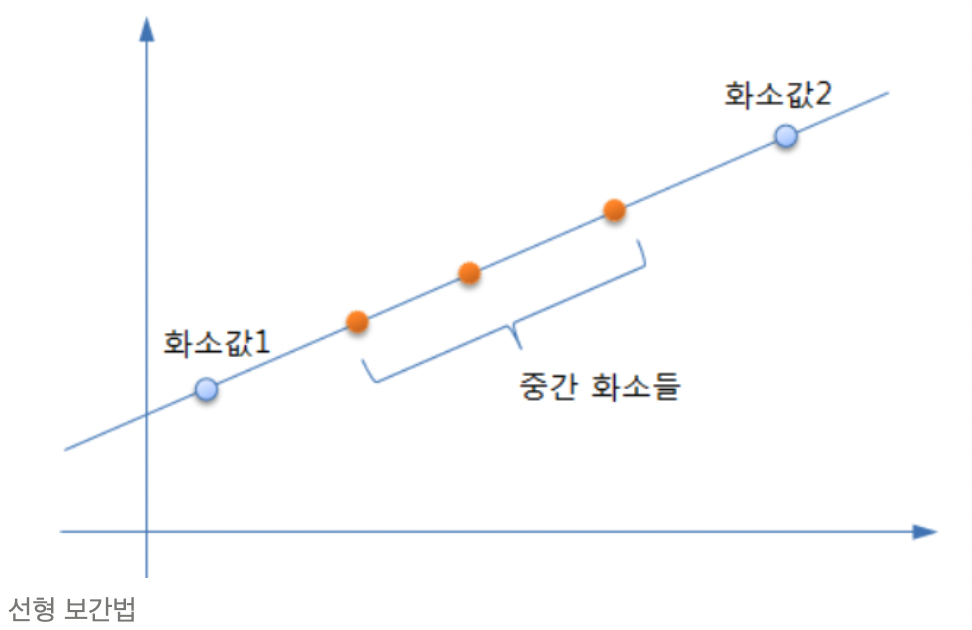
선형 보간법 : 직선의 선상에 위치한 중간 화소들의 값은 직선의 수식을 이용해서 쉽게 계산
양선형 보간법 : 선형 보간을 두번에 걸쳐서 수행.
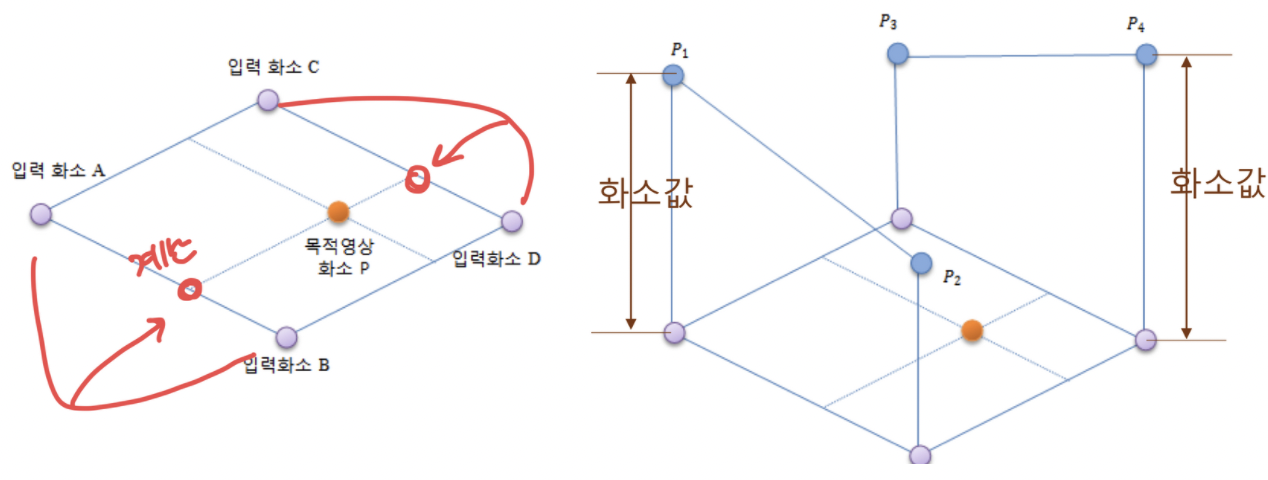
목적영상화소를 역변환으로 계산하여 가장 가까운 위치에 있는 입력 영상의 4개 화소 (A,B,C,D) 값 가져옴
- 4개 화소를 두개씩 (AB) (CD) 묶어서 두 화소의 최소값 (P1, P2, P3, P4)으로 잇는 직선 구성

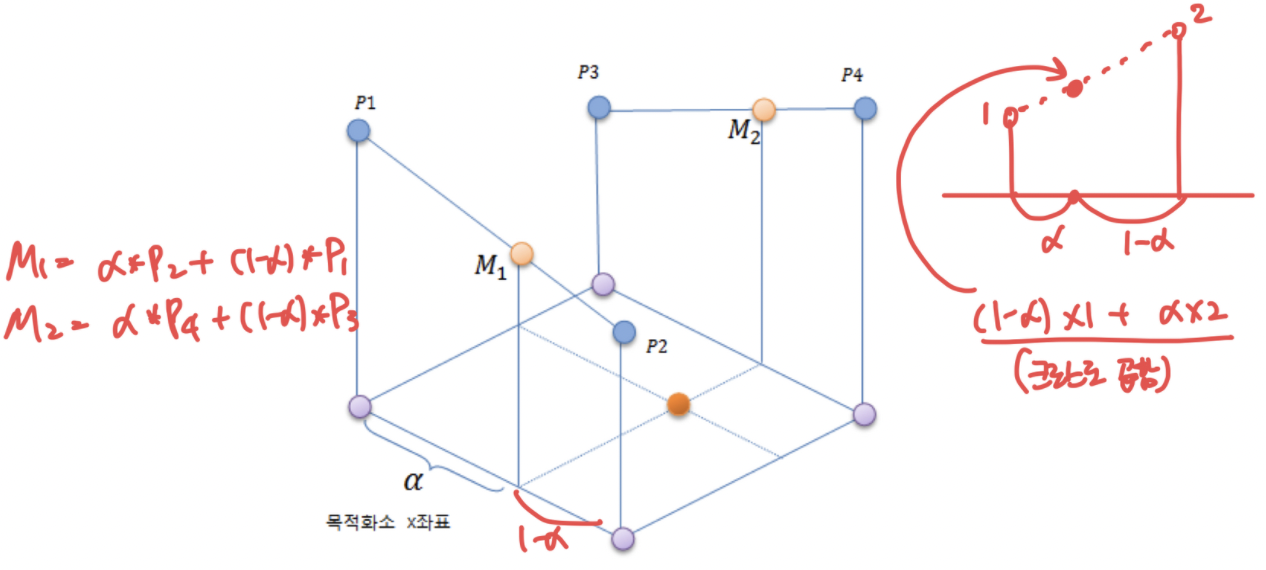
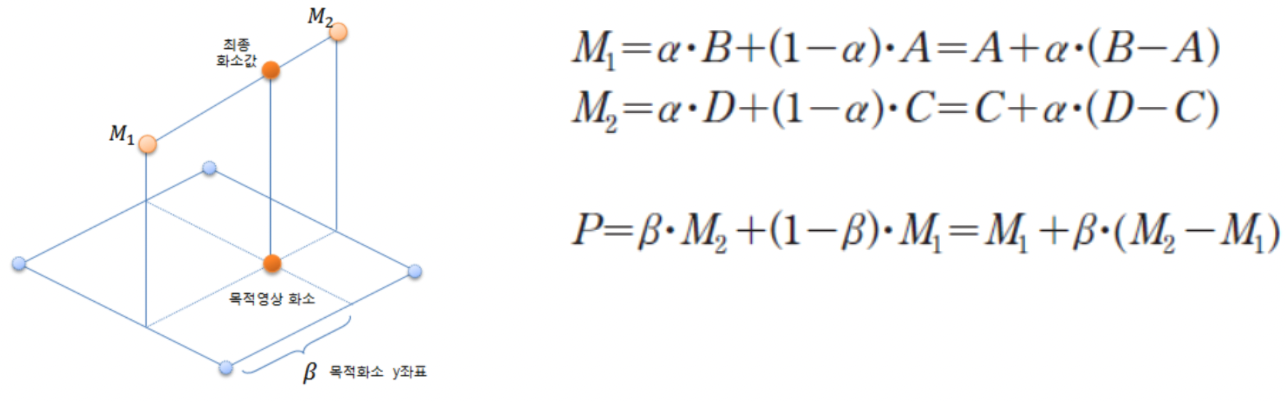
양선형 보간법을 사용해서 영상 확대 구현

import cv2 as cv
import numpy as np

src = cv.imread("Mandrill.bmp", cv.IMREAD_COLOR)
H,W,C = src.shape[:]

ratioX = 2 #row
ratioY = 3 #col

output = np.zeros((H * ratioX, W * ratioY, C), src.dtype)


for xd in range(H*ratioX):
   for yd in range(W*ratioY):
        for L in range(3):
            x = xd / ratioX
            y = yd / ratioY

            X = int(x)
            Y = int(y)

            beta = x - X
            alpha = y - Y

            #양선형 보간
            if (-1 < X < H and -1 < Y < W and -1 < X + 1 < H and -1 < Y + 1 < W):
                # 가로방향 보간
                mid1 = (1 - alpha) * src[X][Y][L] + alpha * src[X][Y + 1][L]
                mid2 = (1 - alpha) * src[X + 1][Y][L] + alpha * src[X + 1][Y + 1][L]
                # 세로방향 보간 (최종값)
                output[xd][yd][L] = beta * mid2 + (1 - beta) * mid1

cv.imshow("input", src)
cv.imshow("output", output)
cv.imwrite('/Users/jiwonheo/bin/python3/Users/jiwonheo/Development/학교 강의/영상정보처리/lab3/Lowpass_filtering_3.bmp', output)
cv.waitKey(0)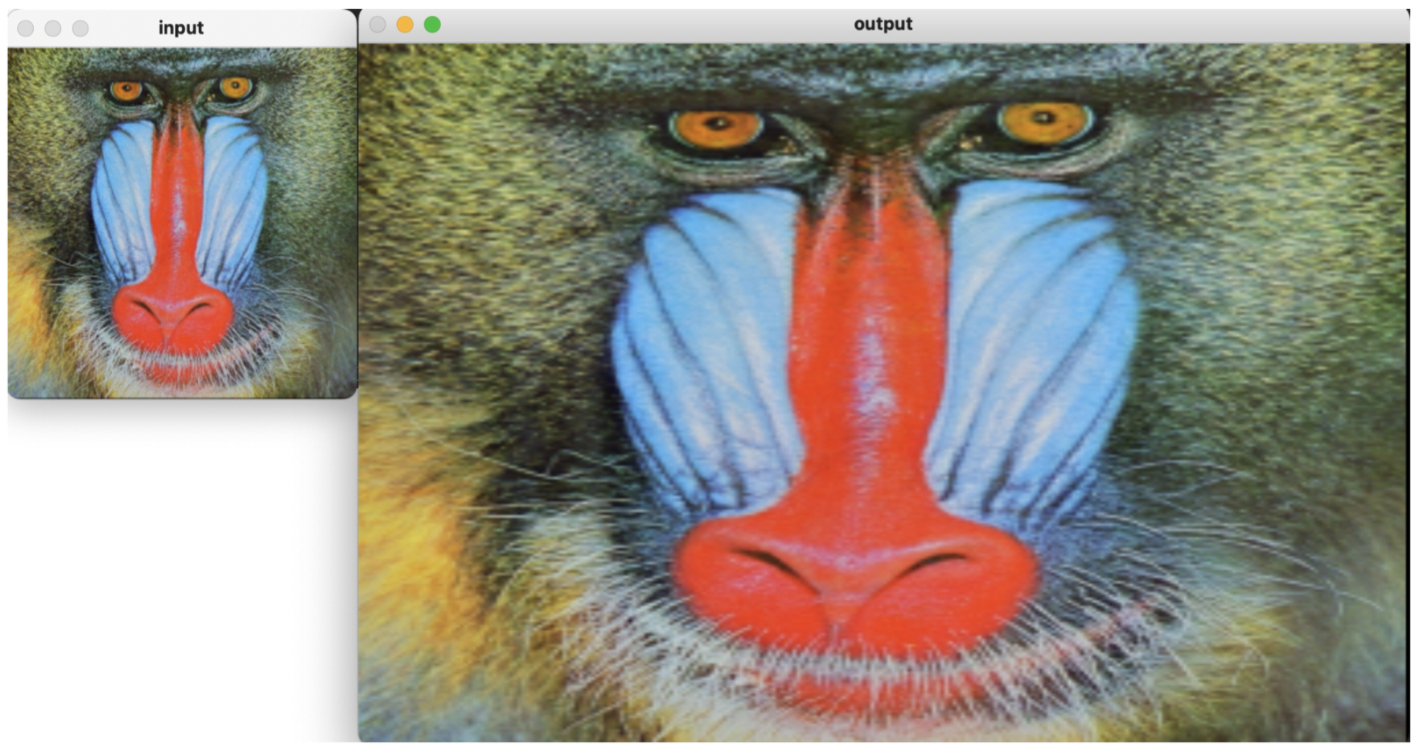

평행이동

영상의 원점을 기준으로 모든 화소를 동일하게 가로방향과 세로 방향으로 옮기는 것
가로 방향으로 dx만큼, 세로 방향으로 dy만큼 전체 영상의 모든 화소 이동한 예

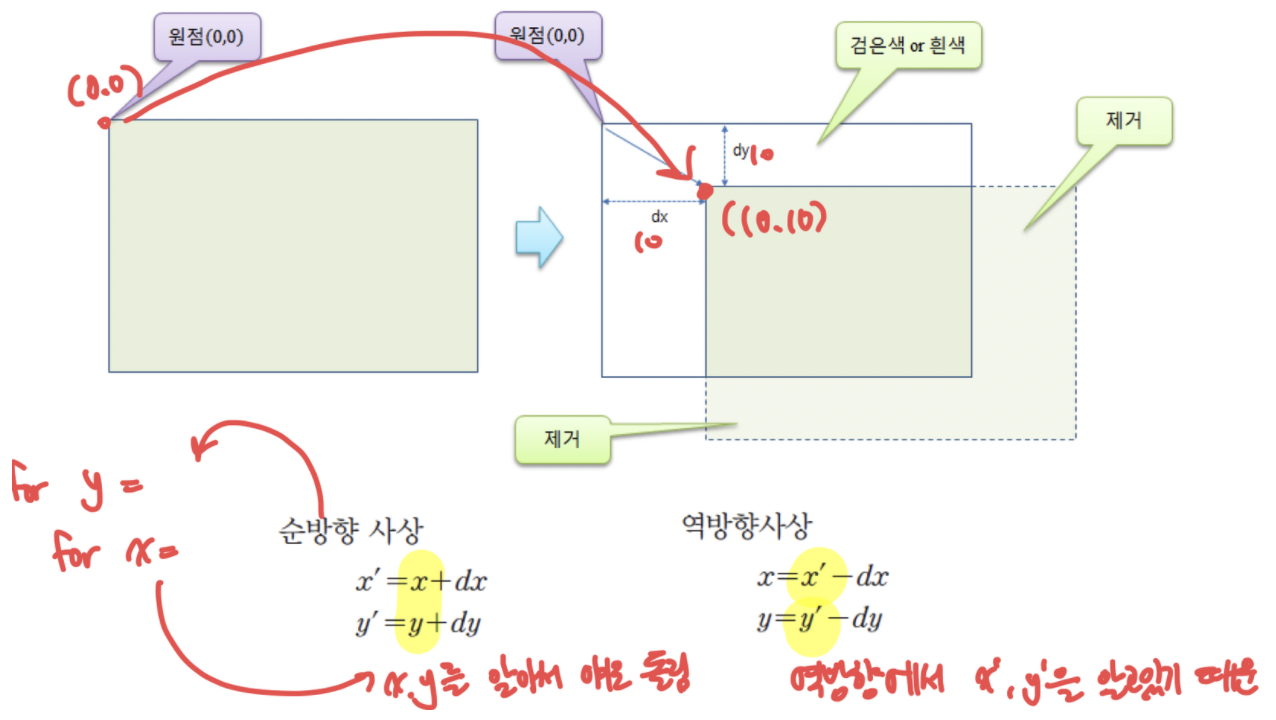
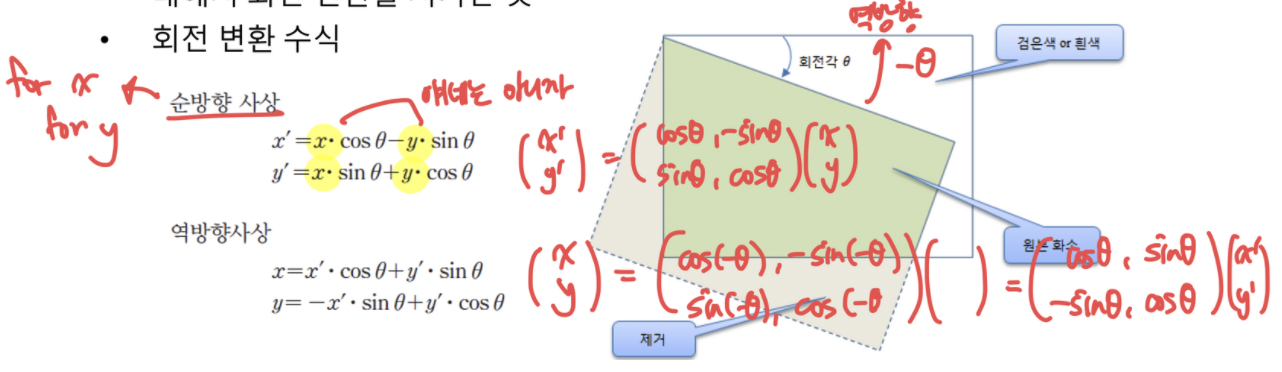
영상의 회전

입력영상의 모든 화소를 영상의 원점을 기준으로 원하는 각도만큼 모든 화소에 대해서 회전 변환을 시키는 것.
회전 방향
- 원점으로부터 시계 방향으로 정해진 각도만큼 회전된 영상 생성
- 직교 좌표계 - 반시계 방향
- 영상 좌표계 - 시계방향 (y 좌표가 하단으로 내려갈수록 증가하기 때문)

특정 좌표에서 회전하는 경우
- 원점으로 이동 → 회전 수행 → 특정 좌표로 이동

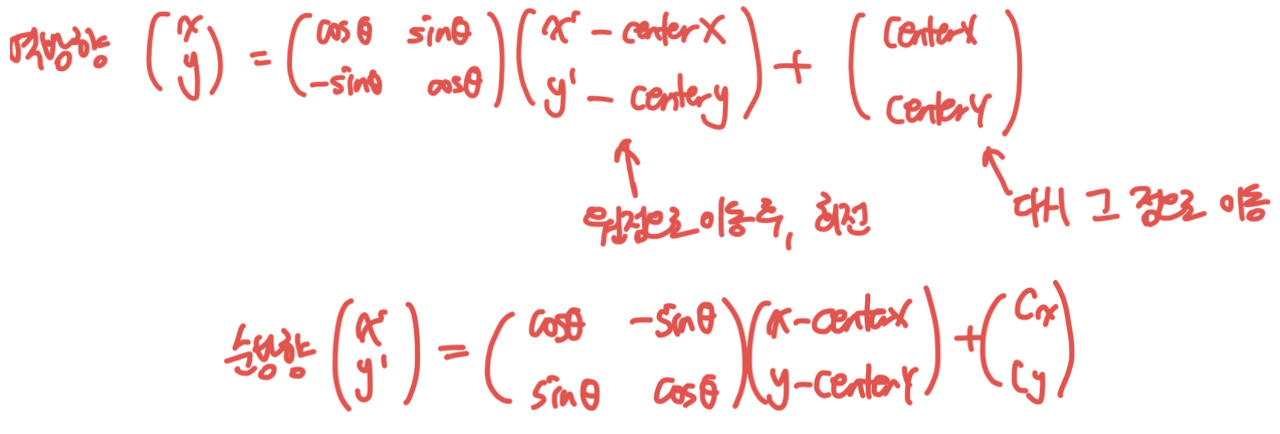
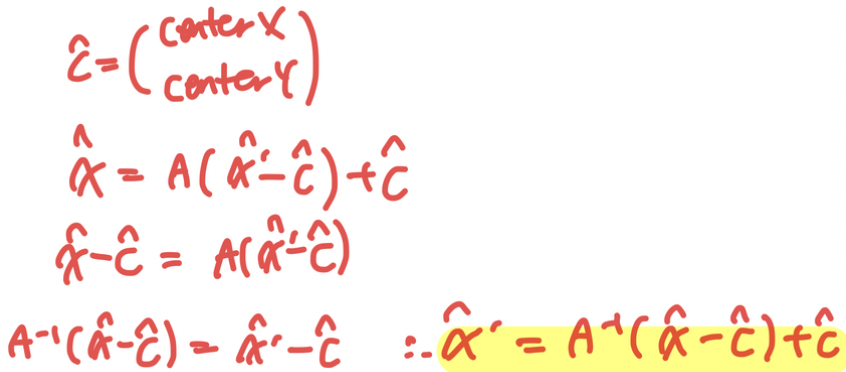
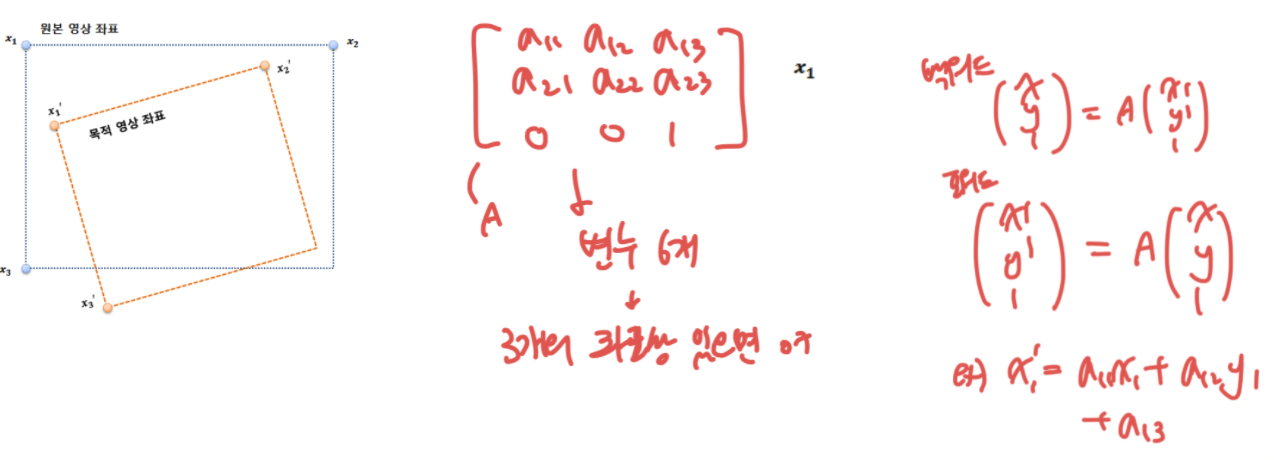
행렬 연산을 통한 기하학 변환 - Affine Transform

입력영상의 좌표 3개( x1 , x2 , x3)와 변환이 완료된 목적영상에서 상응하는 좌표 3개( x1, x2, x3)를 알면 → 어파인 행렬 구성 가능

원근 투시 변환 – Perspective Transform (투영변환)

동차 좌표계(homogeneous coordinates)
- ← 계산을 편하게 하려고 차원 확장
- 모든 항의 차수가 동일하기 때문에 붙여진 이름으로서 n차원의 투영 공간을 n+1개의 좌표로 나타내는 좌표계
  - 직교 좌표인 ( x, y )를 ( x, y, 1 )로 표현하는 것
  - 일반화해서 0이 아닌 상수 w에 대해 ( x, y )를 (wx, wy, w)로 표현
  - 상수 w가 무한히 많기 때문에 ( x, y )에 대한 동차 좌표 표현은 무한히 많이 존재
동차 좌표계에서 한 점(wx, wy, w)을 직교 좌로 나타내면
- 각 원소를 w로 나누어준 (x/w, y/w)가 됨
- 예, 동차 좌표계에서 한 점(5, 7, 5) → 직교 좌표에서(5/5, 7/5) 즉, (1, 1.4)
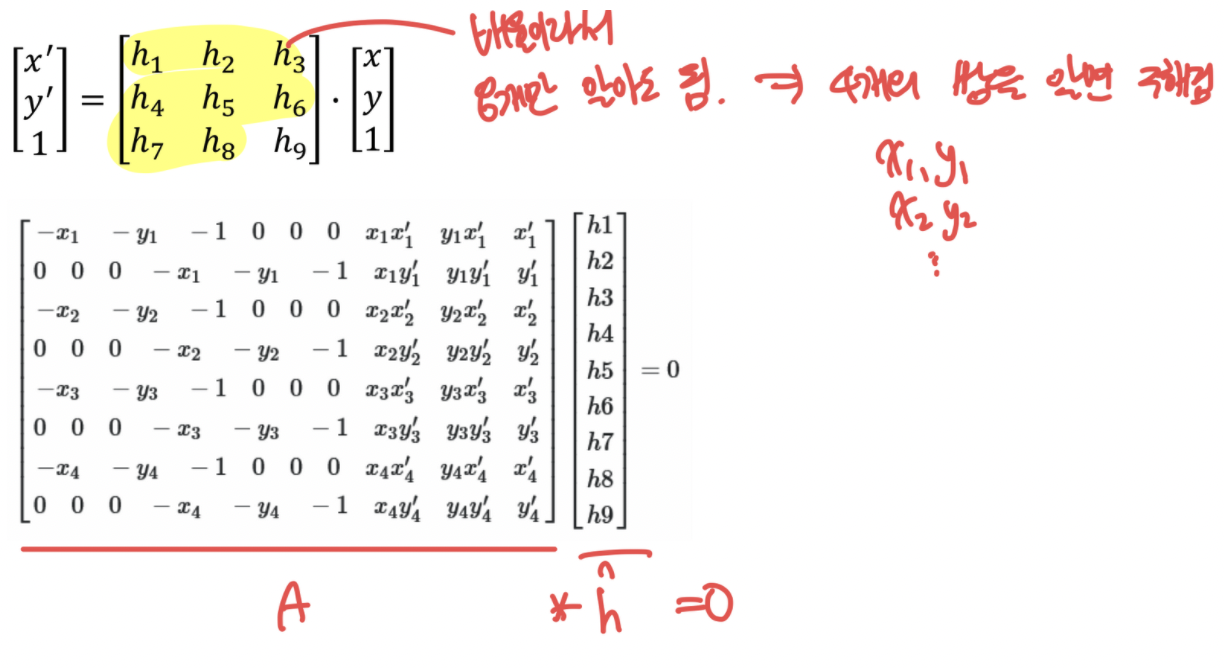
원근 변환을 수행하는 행렬 (Homography)