경희대학교 황효석 교수님의 2021-2 로봇 프로그래밍 수업을 듣고 공부한 것입니다.
Kalman Filter
칼만 필터는 노이즈, 센서의 정확도 등 확률 분포를 가우시안으로 표현한 것이다. 가우시안은 mean 과 distribution 값만 있으면 확률 분포를 알 수 있기 때문에, 매우 편리한 도구이다.
하지만 가우시안은 모든 연산이 선형적이어야 계속 적용 및 유지 가능하다는 단점을 갖고 있다.
만약 가우시안 분포를 갖는 데이터에 어떤 transform 을 적용 했을 때, 결과값도 가우시안 분포이려면 이 transformation 이 linear 해야 한다는 뜻이다.
하지만 현실 세계의 여러가지 문제들은 linear 하지 않은 것이 대부분이다. (sin, cos, e^x 등등)
따라서 칼만 필터를 적용할 때 이런 문제점에 맞닥뜨리게 된다.
칼만 필터는 모든 확률분포가 linear 하다는 것을 가정하는데, 우리가 현실세계에서 다루는 확률분포는 non-linear 한 것이 대부분이다.
해결책 1
-> 그러면 비선형적인 시스템에 대해서는 칼만 필터를 쓰지 말자. (Partical Filter 의 아이디어)
해결책 2
-> 전체적인 시스템은 내비 두고, 어떠한 국소 부위와 그 주변만 선형적으로 만들고 적용하면 되지 않을까?
-> Local Linearization!
Linearization
A Taylor Series is a series expansion of a function about a point.
EKF (Extended Kalman Filter) uses first-order series expansion.
f(x) = f(a) + f'(x-a)
Jacobian Matrix
야코비안은 다음과 같이
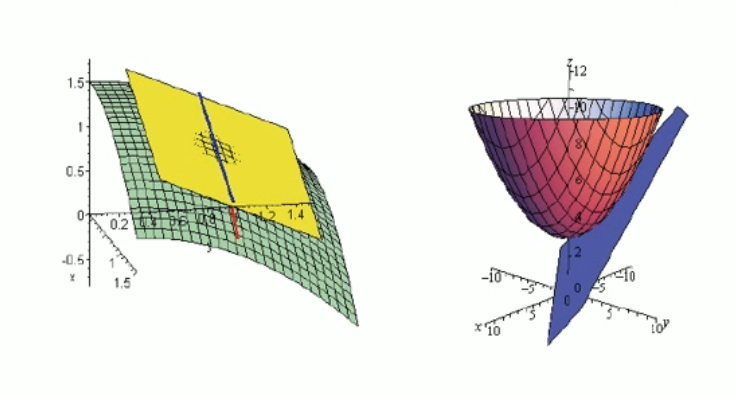
야코비안 행렬이 말하고자 하는 것은 미소 영역에서 비선형 변환을 선형 변환으로 근사시킨다는 것이다.
Taylor series
어떤 점을 기준으로, 무한히 미분할 수 있는 함수가 있을 때 특정 파라미터로 표현하기 어려운 함수도 근사화한 급수로 표현할 수 있다.
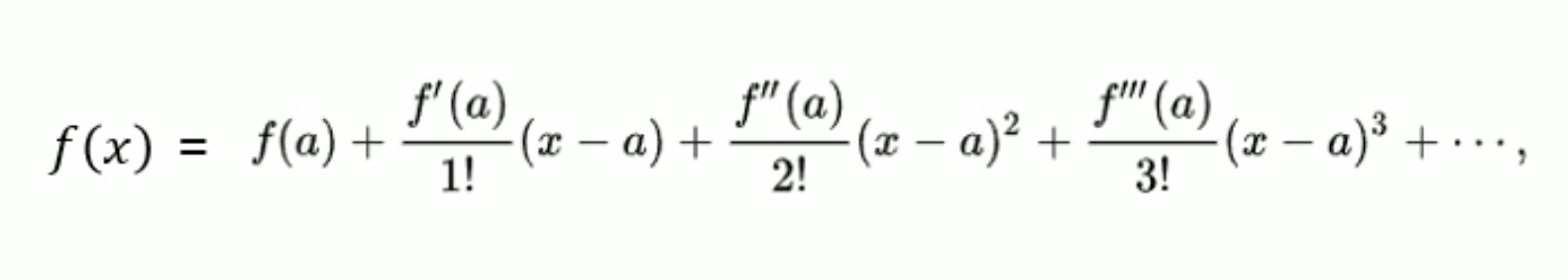
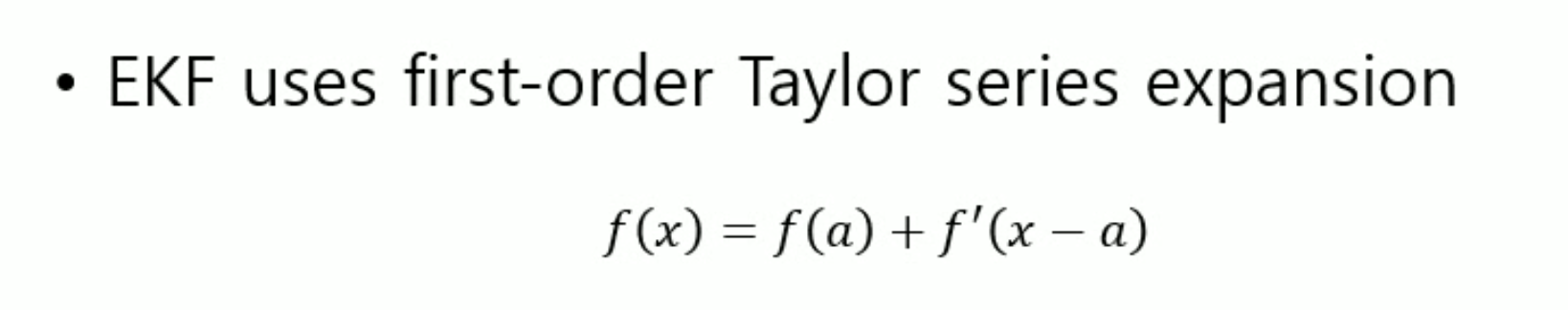
Jacobian Matrix
non-linear function 이 있을 때 first-order Taylor series expansion 을 사용하려면
- 1차 도함수 (Jacobian Matrix) 를 계산해야 한다.

자코비안 행렬은 모든 연산에 대해서 각각의 항으로 편미분을 한 것이다.
이를 물리적으로 해석하면 어떤 지점에서의 법면을 의미한다.
- EKF 에서의 Prediction 과 Correction
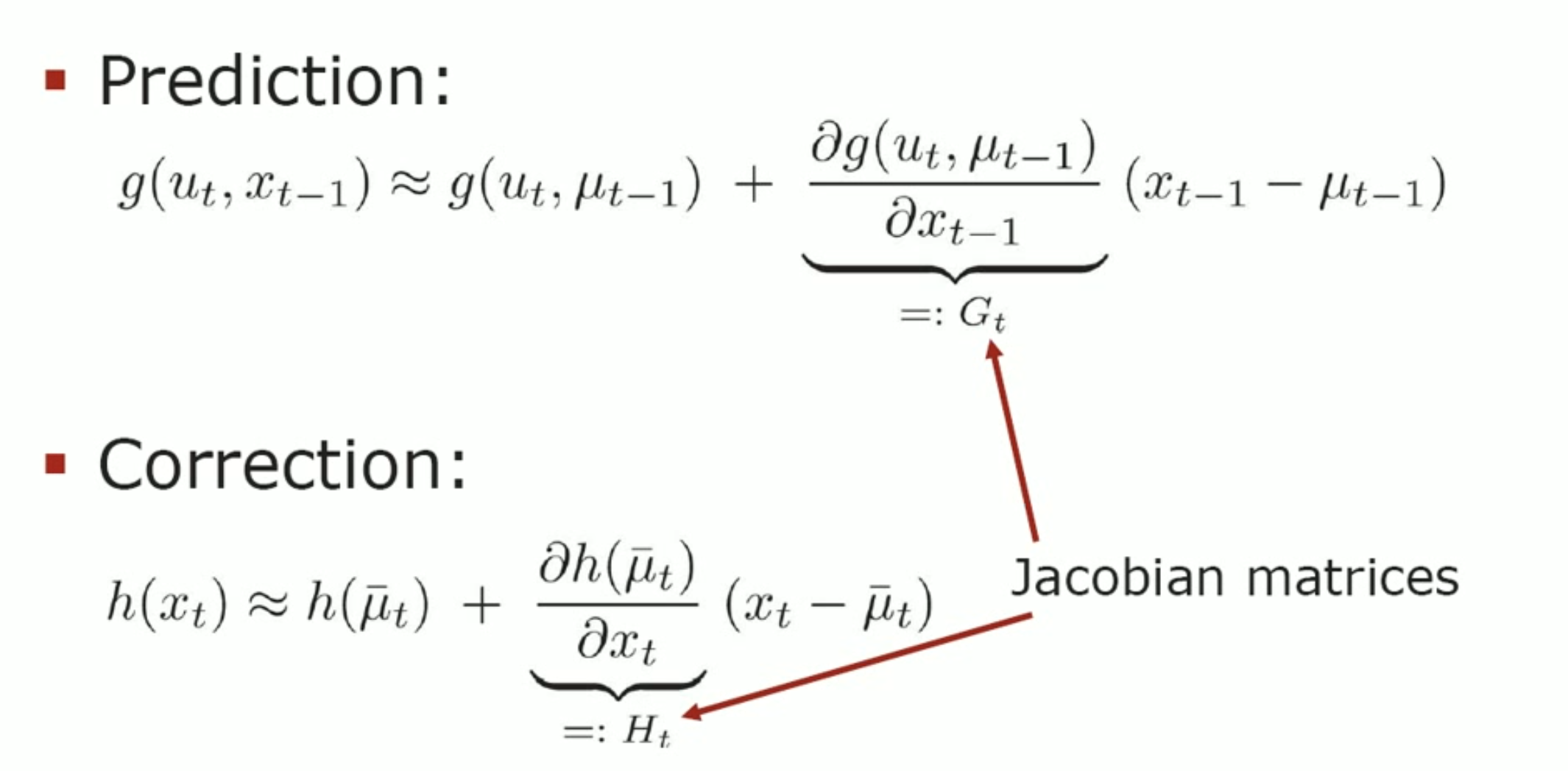
u (t-1) 은 이전 distribution 의 mean 값이다. 이전 mean 을 기준으로 이 주변에 있는 값들은 선형변환을 통해서 옮길 것이다.
Correction 도 마찬가지로, 평균값을 중심으로 해서 H (non-linear function) 의 Jacobian Matrix 를 구하고, 거기에 (xt-ut) 를 곱함으로써 기존 입력의 distribution 을 선형으로 변환하는 효과를 가지게 된다.

