본 게시글은 데이터 과학 기초 수업을 듣고 정리한 글로, 참고 용도 정도로만 이용하시면 좋을 것 같습니다.
오늘은 탐색적 데이터 분석 Exploratory Data Analysis에 대해 살펴보자
탐색적 데이터 분석이란?
탐색적 데이터 분석(Exploratory Data Analysis)은 데이터에 대한 기본적인 이해를 하기 위한 탐색과 분석과정을 말한다. 이러한 EDA는 데이터의 기본적인 유형,구조,분포,관계 등을 파악하기 위해서 사용된다.
여기서 분포에는 예를 들어 정규분포,가우시안 분포 등등이 있겠고, 관계는 상관관계 등등에 대해 말하는 것이다. 이에 대해서도 이후 포스팅에서 다룰 것이다.
기술통계란?(Descriptive Statistics)
데이터의 정리,요약,해석,표현을 통해 자료의 특성을 규명한다.
도수분포표,평균,분산 표준편차,상관계수 등이 있다.
데이터 시각화란?(Data Visualization)
시각적 도구를 이용한 데이터의 이해 방법이다.
데이터 시각화 도구에는 산점도(Scatter plot), 히스토그램, 선/막대 그래프, 상자 플롯, 파이 차트 등등이 있다.
데이터의 유형: Data Types
숫자형(연속형, 양적 자료):Numeric(Continuous, Quantitative)
-수치로 나타낼 수 있는 변수. 산술/논리 연산을 적용할 수 있다.
평균,분산,표준편차,분포 등이 주요 분석 대상이다.
범주형(명목형, 질적 자료):Categorical(Nominal, Qualitative)
-기호나이름으로 구분할 수 있는 변수. 산술/논리 연산을 적용할 수 없다.
빈도,히스토그램(histogram) 등이 주요 분석 대상이다.
변수란? Variables
통게학에서 말하는 변수는 연구,조사,관찰하고 싶은 대상의 특징을 말한다.
키,몸무게,혈액형,매출액,온도,습도,미세먼지 노도 등을 말한다.
단일 변수 데이터: Univariate Data
-일변량 자료를 말하고 일변량 자료는 하나의 변수로만 구성된 데이터를 말한다.(벡터)
다중변수 데이터: Multivariate Data
-다변량 자료를 말하고 다변량 자료는 두 개 이상의 변수로 구성된 자료를 말한다.(행렬, 데이터 프레임)
변수의 종류:(문제에서 바꿔내기 좋기 때문에 중요!)
목적 변수(종속 변수=설명변수):Target(Dependent) Variable
-어떤 분석을 통해 추정하거나 예측하고자 하는 목적이 되는 데이터
-독립 변수의 값이 변화에 따라 영향을 받는 종속 변수
특징 변수(독립 변수):Feature(Independent) Variable
-목적 변수의 추정이나 예측을 위해 사용하는 데이터의 특성
-종속 변수의 값에 독립적으로 영향을 주는 변수
결국 구하고자 하는 값은 목적 변수인 것이다!
저번 포스팅에서 언급했던 고흐의 붓꽃 문제 다들 기억나시나요?
그 IRIS dataset에 대해 자료를 살펴봅시다!
IRIS dataset: 우선 두개 이상의 변수로 구성된 자료이기 때문에 다변량 자료입니다.
Features:4개의 numeric 독립변수
sepal length, sepal width, petal length, petal width
Targets:범주형 종속변수(이 값을 예측해서 찾아내겠죠?)
-iris:붓꽃의 품종(3종)
연속형 자료의 탐색과 분석:
평균:전체 변량의 총합을 변량의 개수로 나눈 값
-(평균)=(변량)의 총합/(변량)의 개수
중앙값:자료의 변량을 순서대로 나열할 때, 중앙에 위치하는 값
-매우 크거나 작은 값이 있을 경우에는 평소보다 더 자료의 특성을 더 잘 반영.
분산:편차를 제곱한 값의 평균, 표준편차: 분산의 양의 제곱근
-(분산)=(편차)^2의 총합/(변량)의 개수, (표준편차)= 루트(분산)
-분산(표준편차)의 값이 클수록, 평균을 중심으로 흩어져 있는 정도가 크다.
-분산(표준편차)의 값이 작을수록, 평균을 중심으로 흩어져 있는 정도가 크다.
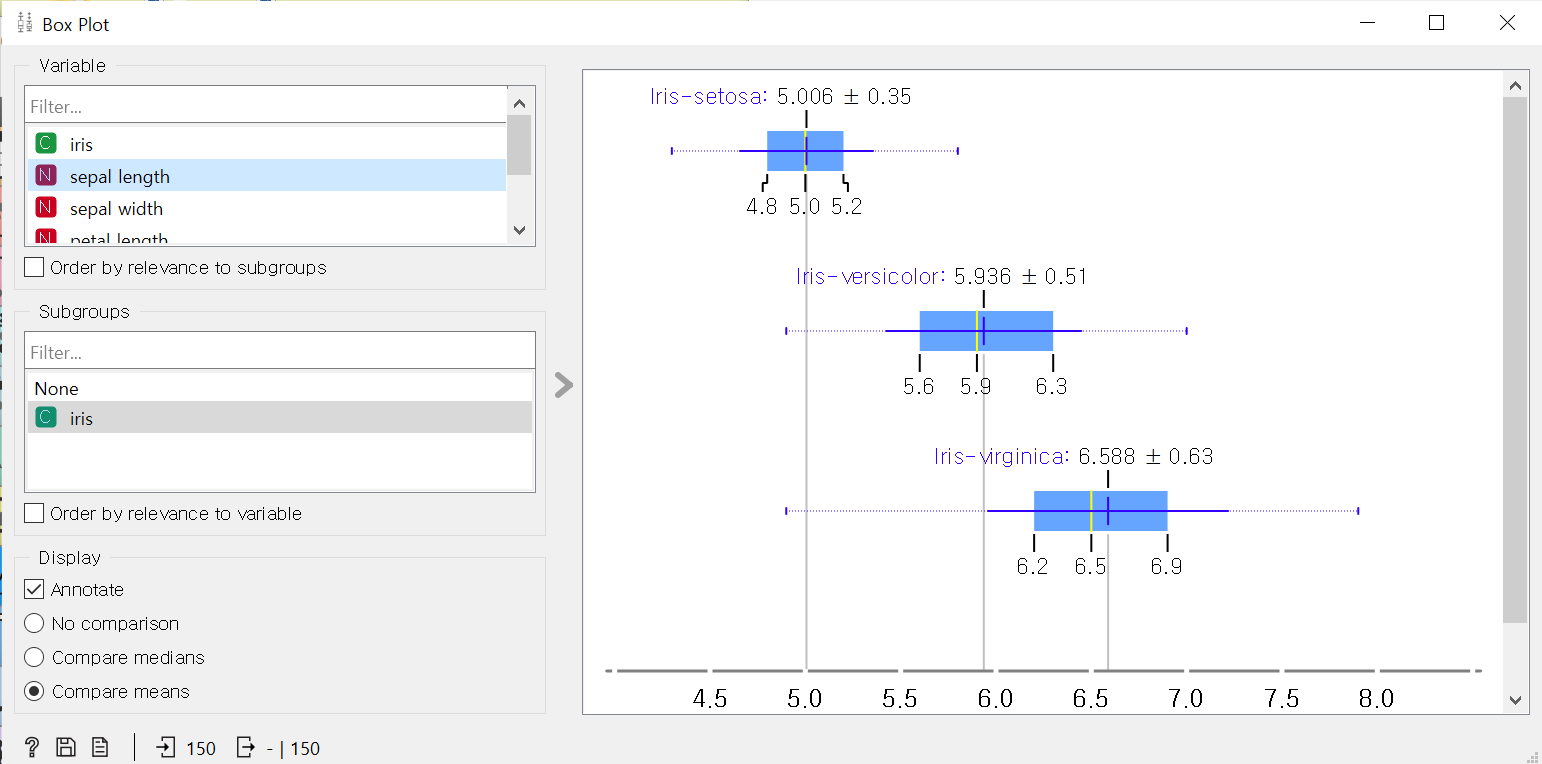
이러한 연속형 자료를 살펴보기 위해서는 orange에서 box plot을 사용하면 된다.
다음과 같은 box plot의 iris-setosa의 경우 5.006이 평균이고 5.0이 중앙값 4.8이 최소값 5.2가 최댓값이다.
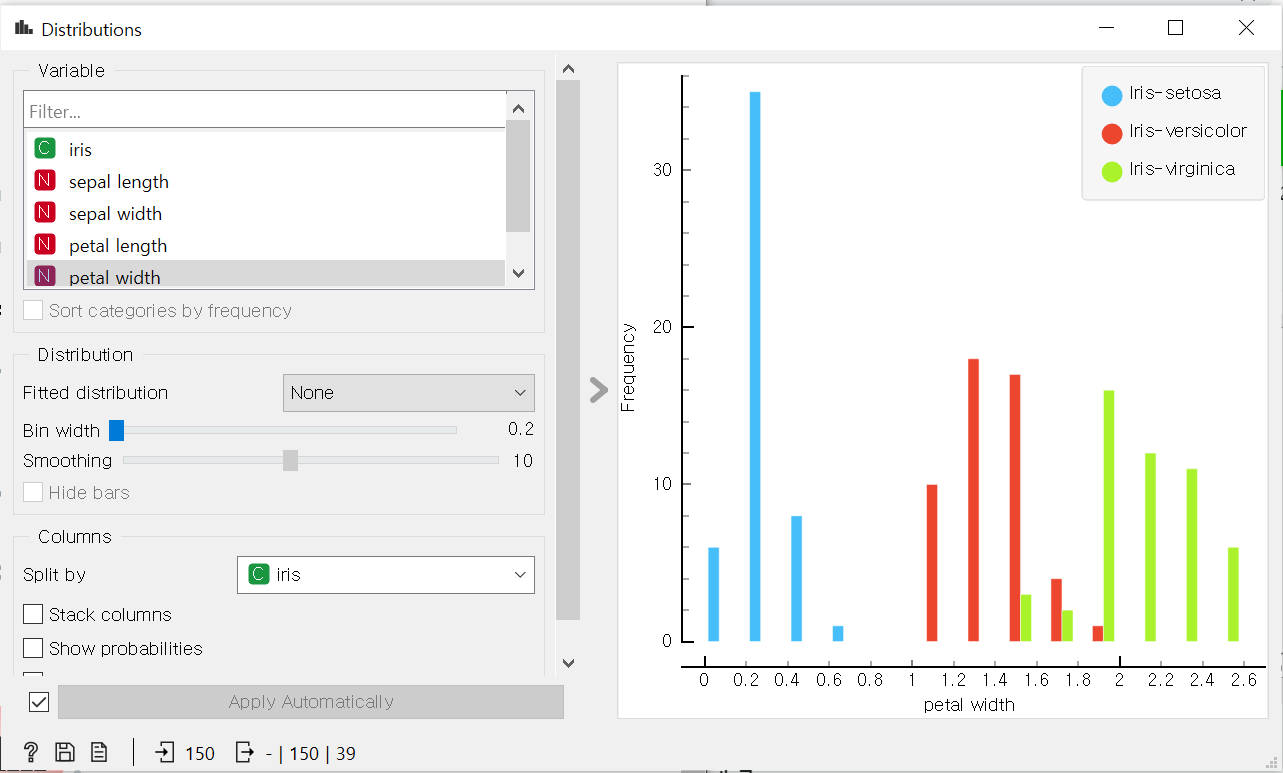
범주형 자료의 탐색과 분석:frequency
범주형 자료는 평균,분산,표준편차 등의 통계적 특성을 가지지 않는다.
-각 변수의 빈도(frequency)를 막대 그래프 등으로 파악한다.
도수분포표:데이터를 정리하여 도수의 분포를 표로 나타낸 것이다
-도수: 각 구간에 속하는 자료의 수이다.
히스토그램(histogram): 도수분포표를 그래프로 나타낸 것이다.
orange를 통해 범주형 자료에 대해 다음과 같이 살펴볼 수 있다.
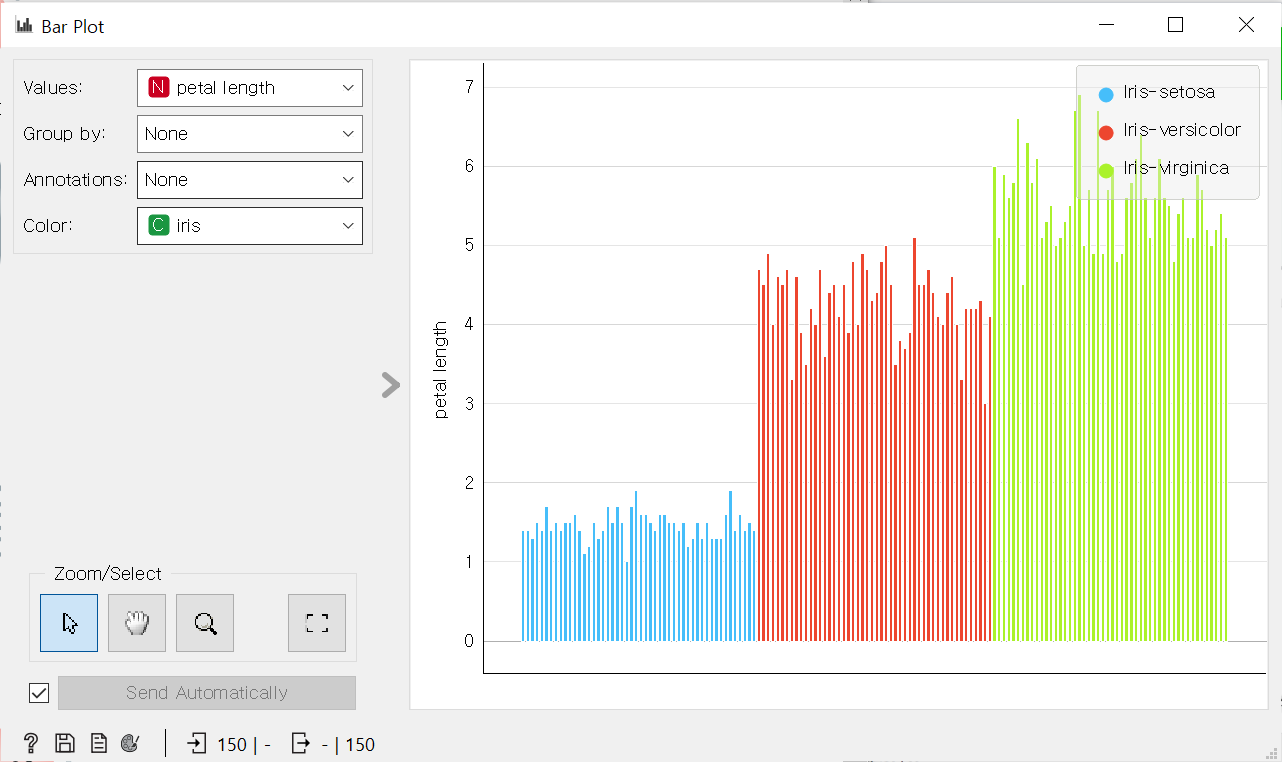
데이터시각화:Data Visualization
숫자형/범주형 데이터를 그래프나 그림등의 시각적 형태로 표현하는 것
탐색적 데이터 분석과정에서 데이터를 파악하는 중요한 기술 중의 하나이다.
주요 시각화 방법:선그래프,막대그래프, 히스토그램, 박스플롯, 산점도,모자이크플롯,히트맵 등등
산점도: Scatter Plot
두개의 변수로 구성된 자료의 분포를 알아보는 그래프
관측값들의 분포를 통해 두 변수 사이의 관계를 파악할 수 있다.
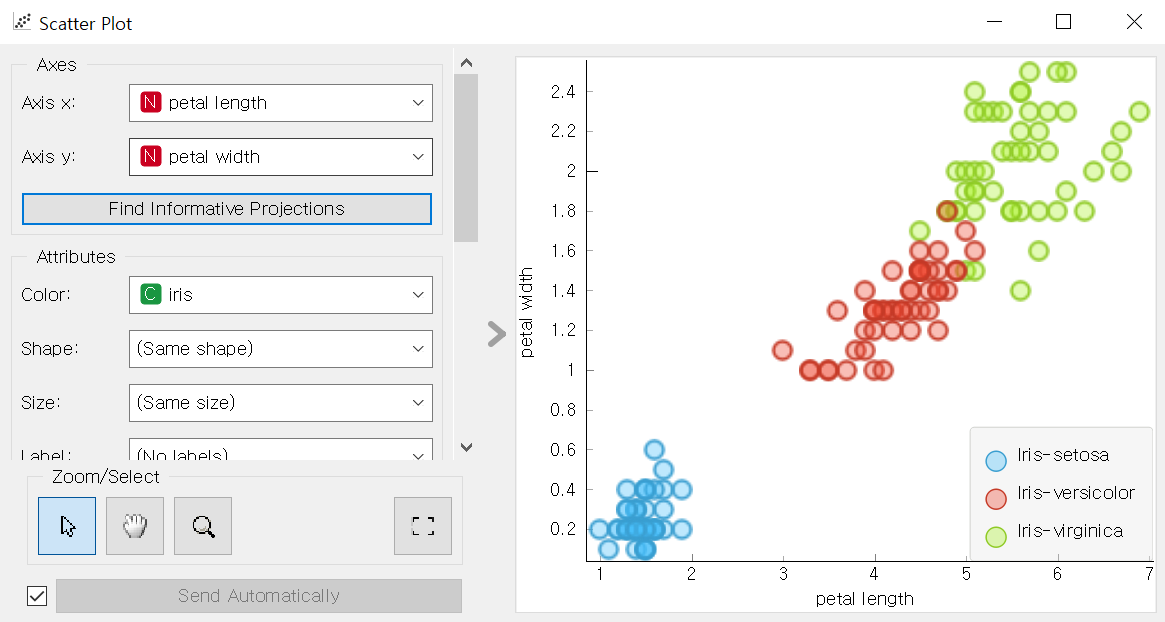
상관 분석:Correlation Analysis
두 변수 간에 어느 정도의 선형적 관계가 있는지를 파악하는 방법.
상관계수:Correltaion Coefficient
-상관 관계의 정도를 나타내는 지수
피어슨 상관 계수:Pearson's Correlation Coefficient
-두개의 데이터 X,Y에 대해서, (x1,y2)(x2,y2),...,,(xn,yn)
-X와y가 함께 변하는 정도/ x와 y가 각각 변하는 정도
-수식: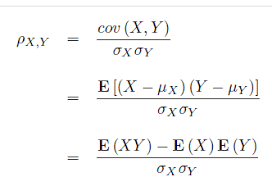 
피어슨 상관계수에 대한 해석을 알아보자
0<r<=1:양의 상관 관계가 있다. x가 증가하면 y도 증가한다.
-1<=r<0:음의 상관 관계가 있다. x가 증가하면 y는 감소한다.
r의 절대값이 클수록 두 변수 x,y의 선형적인 상관성이 높다.
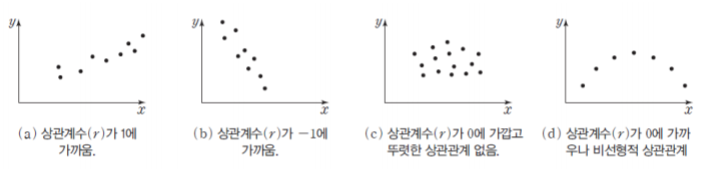
여기서 주의해야할 부분은 상관관계는 인과관계를 의미하지 않는다는 것이다.
상관관계!=인과관계
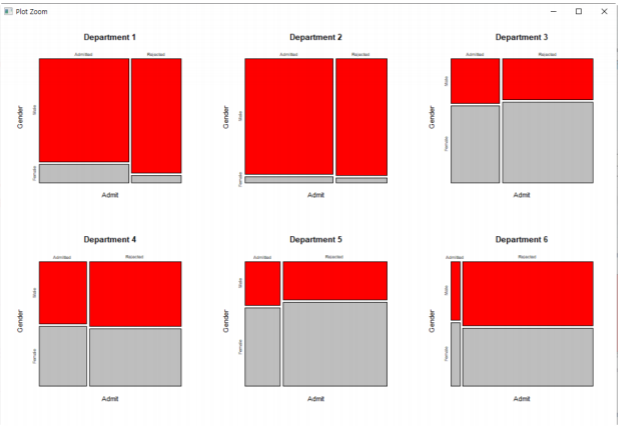
모자이크 플롯:Mosaic Plot
다중 변수 범주형 데이터에 대해 각 변수의 그룹별 비율을 면적으로 표시한 것
UCBAdmissions:1973년 UC버클리 대학의 대학원 입학자료에서 성별,합격 여부,지원학과 등 3개의 변수로 구성된 자료에 대해 모자이크 플롯을 적용하여 자료를 분석하였더니 성차별이 존재하는 것 처럼 나왔다.
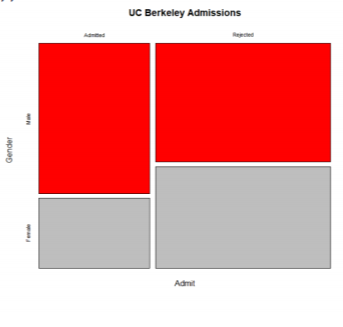과연 UC버클리 대학에서 실제로 합격 여부에 성차별적 요인이 존재한 것일까? 이는 심슨의 역설로 해결할 수 있다.
우선 심슨의 역설(Simpson's Paradox)는 어떤 상관관계의 방향이 혼동요인에 의해 완전히 뒤집어지는 현상을 말한다.
위의 자료를 각 학과별로 나눠서 자료를 다시 분석해보면 어떻게 될까?
다음과 같이 심슨의 역설에 의해 자료에 대한 성차별적 요인은 없다는 것이 밝혀졌다. 오히려 여성의 합격률이 더 높은 학과도 있기에,,!
