4번째 포스팅이다,, 앞으로 개념이 점점 어려워지는 것같지만 이해만 하고 수식 계산은 다루지않기 때문에,,ㅎㅎ 어렵다고 징징대는 것도 좀 ㅎ~열심히하자!
본 게시글은 데이터 과학 기초 수업을 듣고 정리한 글로, 참고 용도 정도로만 이용하시면 좋을 것 같습니다.
데이터 전처리란 무엇일까? Data Preprocessing
데이터 수집을 통해 확보한 데이터를 정제하고 가공하는 과정
데이터의 정제와 가공: 데이터의 선택,분리,병합,샘플링
결측치와 이상치:Missing values and Outliers
-제거하거나, 대체한다
정규화:Normalization
차원축소:Dimension Reduction
-주성분 분석: PCA,Principal Component Analysis
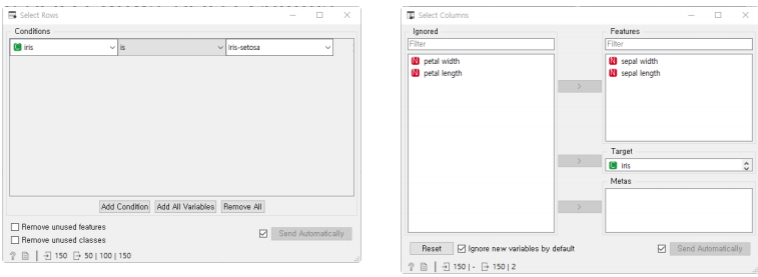
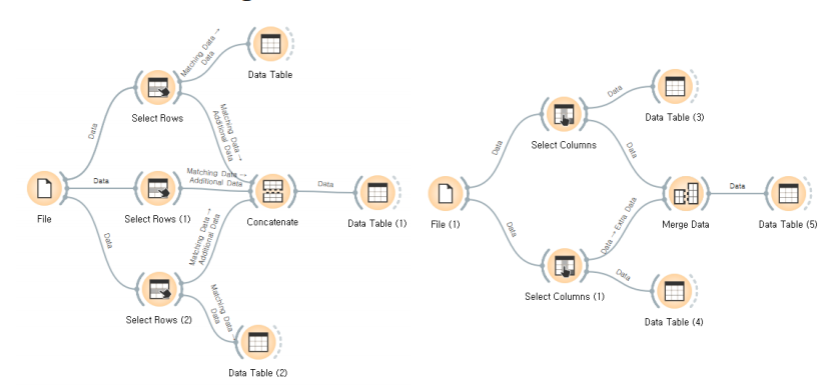
orange에서, select rows 와 select columns로 데이터를 분리하고 Merge,Concatenate로 데이터를 결합한다.
(select rows->concatenate,select columns -> merge data)
데이터 샘플링?: Data Sampling
샘플링: 주어진 데이터에서 임의의 값들을 추출하는 작업
-복원 추출: 추출한 데이터를 다시 포함하여 새로운 데이터를 추출
-비복원 추출: 한번 추출한 데이터는 다시 포함하지 않고 새 데이터를 추출(중복이 없다)
확률에 대해 살펴보자
확률변수:Random Variable
확률 P:어떤 사건이 우연히 발생할 가능성
-P= 어떤 사건이 발생할 수 있는 경우의 수/ 모든 경우의 수
확률변수 X:
-어떤 시행에서 특정 확률로 발생하는 결과를 표현하는 변수
-ex)주사위를 던졌을 때 나올 숫자를 확률 변수 X라고 했을 때, P(X=1)=1/6,P(X=짝수)=1/2
확률분포:Probability Distribution
확률변수의 값에 따라 달라지는 확률의 분포
확률변수 X의 확률분포:
-확률변수 X가 갖는 값과 X가 이 값을 가질 확률 P(X)의 대응 관계
확률밀도함수:PDF,Probability Density Function
-주어진 확률변수의 분포를 나타내는 함수
누적분포함수:CDF, Cumulative Distribution Function
-주어진 확률변수가 특정값보다 같은 확률을 나타내는 함수
확률분포의 유형
연속 확률변수:
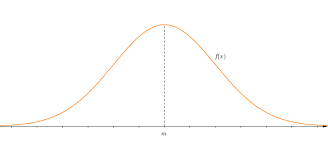
-균일 분포:Uniform Distribution//모든 x에 대해 확률이 똑같다.
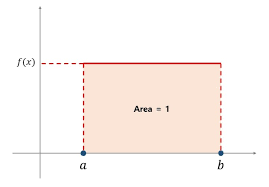
-정규 분포:Normal Distribution (다들 잘 알고 있을 거라 생각한다,, 밑의 그래프만 있는 건 아니고 누적 정규 분포의 형태도 있닷)
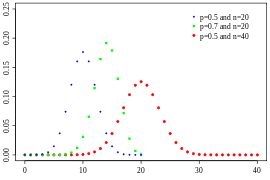
이산 확률변수:
-이항 분포:Binomial Distribution(다음과 같이 연속적이지 않고 이산적인 것을 확인 가능하다.)
멱함수 분포와 롱테일 전략
멱함수 분포:Power-Law Distribution
-P(X)=aX^-k (Zipf의 법칙, Pareto 분포)
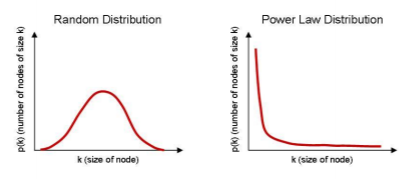
롱테일 전략:Long Tail Strategy
-80:20법칙: 전체 부(매출)의 80%를 상위 20%가 차지한다.
-구글,아마존: 상위 20%보다 하위 80%가 더 많다.
밑의 사진을 보면 조금더 이해하기 쉬울 것 같다.

이상치와 결측치 처리
이상치: Outliers =(특이값)
정상적인 데이터의 분포 범위 밖에 위치하는 값.
실제로 특이한 값일 수도 있고, 오류에 의해 발생한 값일 수도 있다.
몸무게 데이터에서 150kg이 넘는 값이 있다면? 씨름 선수일 수도!
학점 데이터에서 O,X가 있다면->오류!
때로는, 이상치의 발견 자체가 데이터 분석의 목적인 경우도 있다.
제조 공정에서 불량 제품을 선별하려고 하는 경우, 신용카드 회사에서 사기 거래를 탐지하려고 하는 경우(Fraud Detection)
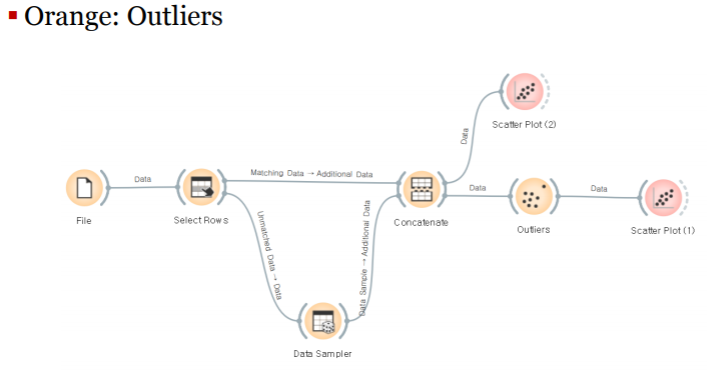
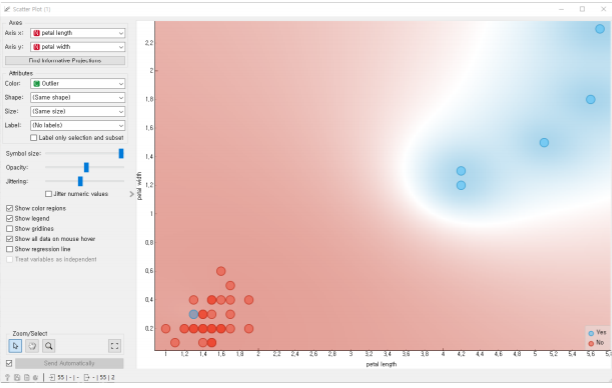
결측치:Missing Values
데이터를 수집하고 저장하는 과정에서 확보하지 못한 값
결측치를 처리하는 두 가지 방법:
-결측치를 포함한 관측값을 모두 제거한다.
-결측치를 추정하여 적당한 값으로 대체한다.
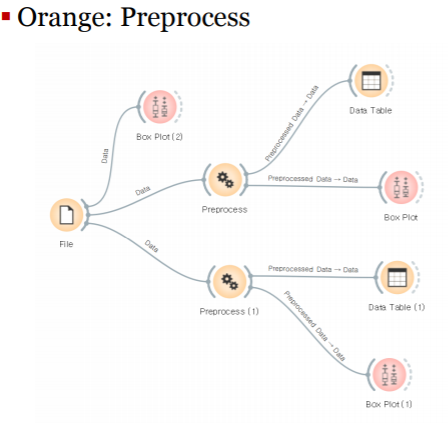
결측치 처리는 orange에서 다음과 같은 workflow를 통해 처리 할 수 있다(impute)
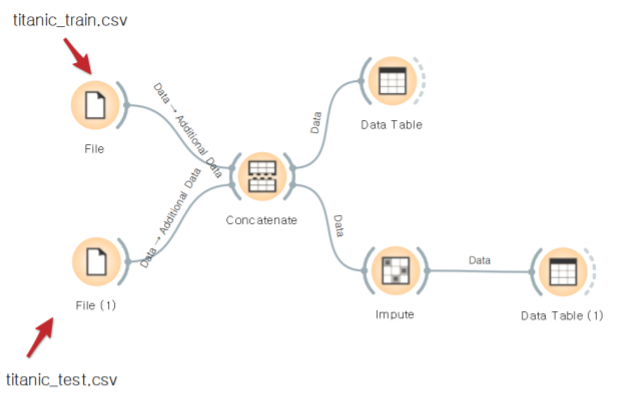
정규화와 차원 축소
데이터 정규화:Normalization
데이터의 특성들이 비슷한 영향력을 행사할 수 있도록 변환해 준다.
단위의 차이, 값의 범위 차이 등으로 인한 차이 발생을 완화한다.
Min-Max정규화:값의 범위를 [0,1]구간에 있도록 변환한다.
- X=(X-MIN)/(MAX-MIN)
Z-Score정규화:값의 분포가 정규 분포를 따르도록 변환한다. - X=X-평균/표준편차
밑의 워크플로우에서의, Preprocess에서 normalize features에서 Standardize to 평=0, 표본^2=1을 선택하면 z-score정규화이고 Normalize to interval [0,1]을 선택하면 min-max정규화이다.
차원 축소: Dimension Reduction
고차원의 데이터를 2차원(또는 3차원)데이터로 축소하는 기법
차원축소가 필요한 이유?:
-시각화:2,3차원의 데이터는 산점도 등으로 시각화 할 수 있다.
-노이즈 제거: feature의 수가 줄어들기 때문에 노이즈도 같이 제거된다.
-성능의 향상:차원의 수가 작으면 처리 속도도 줄어든다.
차원축소의 단점?:
-정보의 손실:차원의 축소 과정에서 정보의 왜곡 손실 현상이 발생한다.
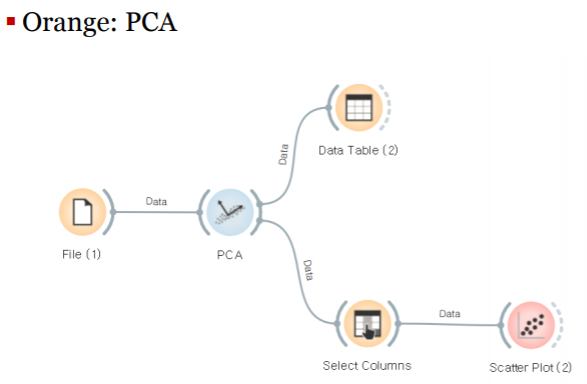
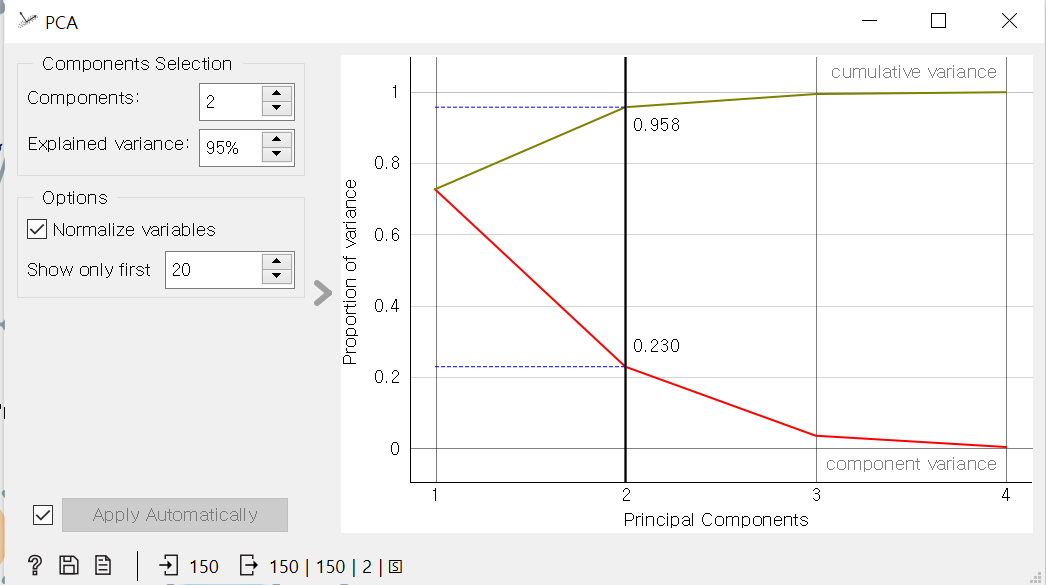
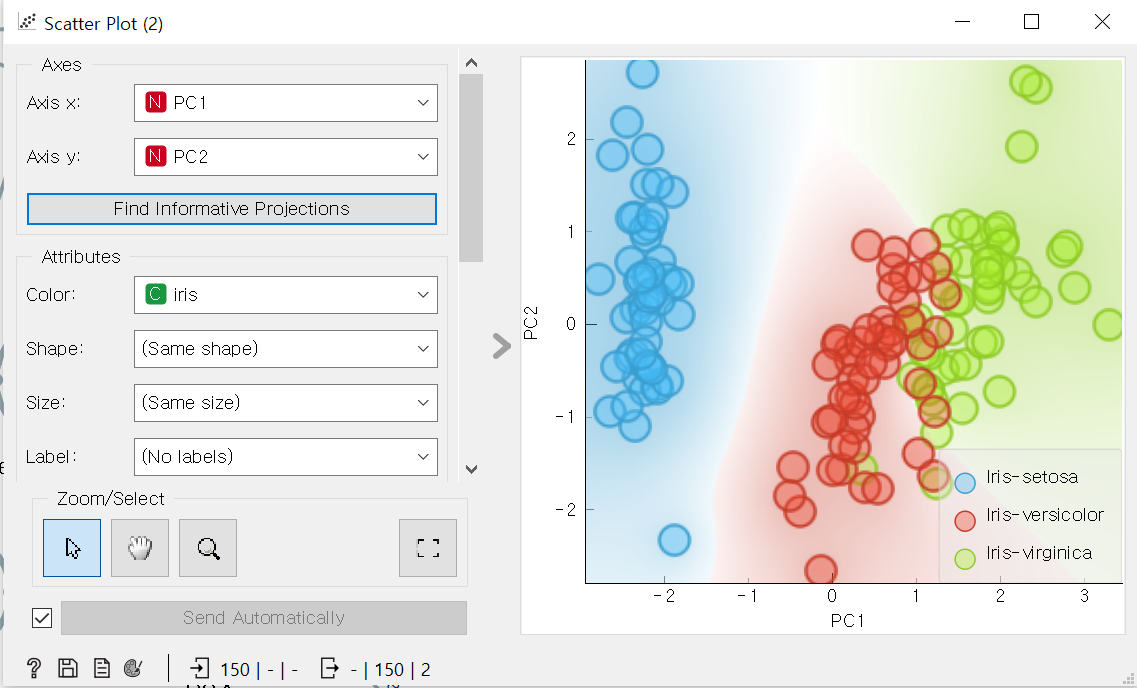
주성분 분석:PCA,Principal Component Analysis
어떤 데이터 분포를 분산이 가장 큰 방향으로 정사영하여 주성분을 구한다.(=주요성분 분석) 고차원->2차원으로
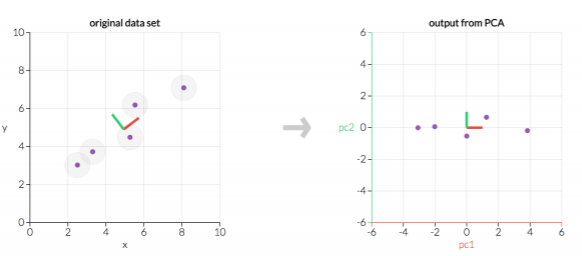
주성분 분석을 orange를 통해 살펴보자