회귀분석과 선형회귀
회귀: Regression
'회귀'의 사전적 의미: 되돌아 가다.
회귀라는 용어의 유래: 프래시스 골턴의 연구에서 처음으로 사용
골턴의 연구 주제: 부모의 키와 자녀의 키는 유전적으로 상관 관계가 있는가?
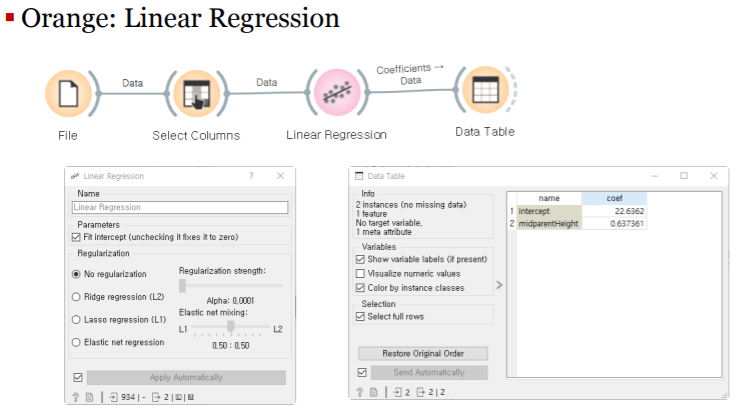
galton데이터 셋을 이용해서 값을 살펴보자:Galton.csv
childHeight: 종속 변수, 자녀의 키
midparentHeight: 독립 변수, 부모의 키
골턴의 업적: 상관과 회귀
회귀의 법칙: law of regression
-부모의 키와 자녀의 키는 선형적인 상관 관계가 성립해야 한다.
평범(평균)으로의 회귀:regression to the mediocrity
-부모와 자녀의 키가 가진 선형 관계의 기울기는 1을 넘지 않아야 한다.
-평균보다 크거나 작은 키는 다음 세대의 평균으로 되돌아 간다.
선형회귀:Linear Regression
두 변량 x,y가 서로 선형적 상관 관계가 있다면?
직선의 방정식으로 이 데이터의 상관 관계를 설명할 수 있을 것이다.
-y=αx+β:α는 기울기(slope), β는 절편(intercept)
회귀 분석:regression analysis
-두 변량 x,y의 관계를 설명하는 회귀식의 기울기와 절편을 찾는 일.
일단, 회귀식을 찾고 나면?
-x의 값이 주어지면 y의 값을 알 수 있다: 예측(prediction)
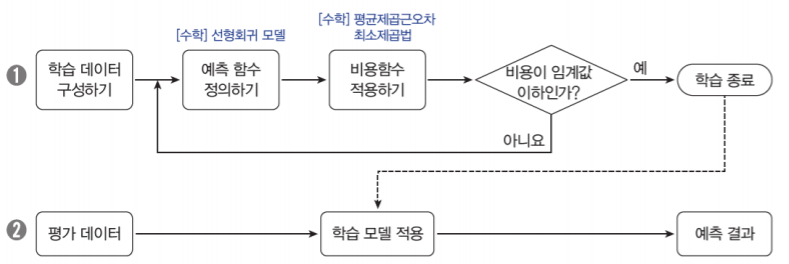
linear regression의 orange 워크플로우는 다음과 같다.
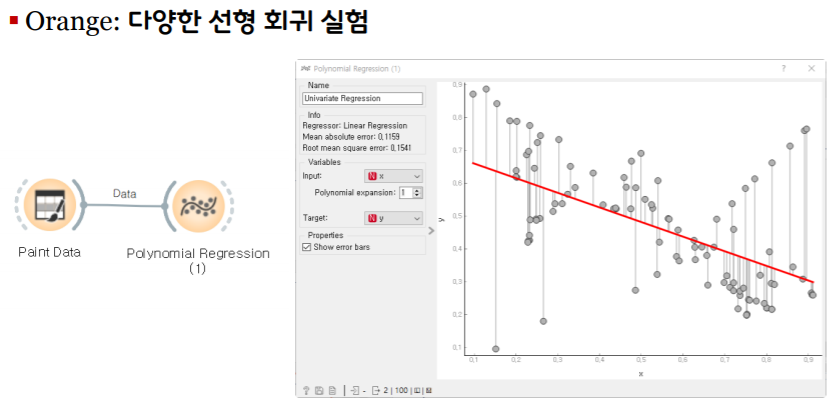
선형회귀식의 학습 방법
회귀식의 기울기와 절편을 찾는 방법은?
-실제값과 예측값의 차이를 최소화하는 기울기와 절편 찾기
비용함수:Cost Function
실제값과 예측값의 차이를 측정하는 함수
-손실 함수:Loss Function
-목적 함수:Objedtive Function
회귀식의 비용 함수를 최소화하는 기울기와 절편을 찾자.
-회귀식의 비용 함수:RSS,MAE,MSE,RMSE
선형 회귀식을 학습하기 위한 과정:
최소 제곱 추정법:LSM, Least Square Method
선형 회귀식의 기울기와 절편을 찾는 가장 일반적인 방법
잔차:residuals
-y의 실제값과 추정값 사이의 수직 거리의 차이:r=y-^y(y hat이다,,)
잔차 제곱합:RSS, Residual Sum of Squres
-잔차는 양수나 음수 모두 가능하므로 잔차의 제곱합을 구함
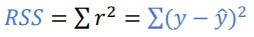
선형 회귀 분석의 목표:
-잔차 제곱합의 값이 최소가 되는 회귀식 찾기!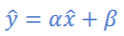
경사하강법: Gradient Descent
비용 함수(예:RSS)가 최소가 되는 기울기와 절편을 구하는 방법은?
- 반족적인 계산을 통해 점진적으로 하강하면서 파라미터를 추정함
어떻게 오류가 작아지는 방향으로 파라미터를 보정할 수 있을까?
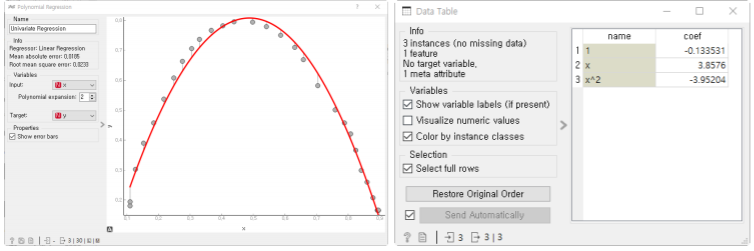
다항 회귀: Polynomial Regrssion
독립변수와 종속변수의 관계가 선형적일 때: y=αx+β
만약, 두 변수의 관계가 2차 방정식, 3차 방정식의 관계라면?
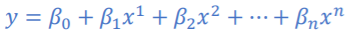
단순 선형회귀와 다중 선형회귀:
단순 선형회귀:Simple(Univariate) Linear Regression
-독립 변수가 하나만 있는 경우: y=αx+β
다중 선형회귀:Multivariate Linear Regression
-독립 변수가 여러 개 있는 경우:
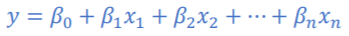
다항 회귀!= 다중 선형회귀
선형 회귀식을 평가하기 위한 지표:
평균 절대 오차: MAE, Mean Absolute Error
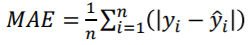
평균 제곱 오차: MSE, Mean Square Error
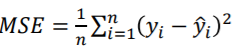
평균 제곱근 오차:RMSE,Root Mean Square Error
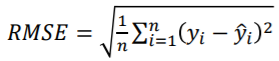
결정계수:R^2,R-Squared, Coefficient of Determination
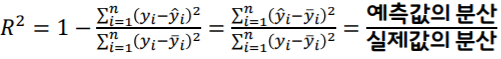
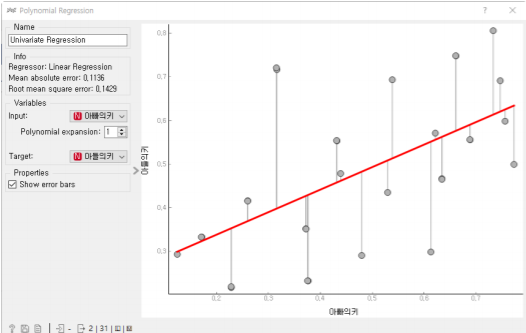
선형회귀식 값들을 살펴보기 위한 orange workflow이닷
더 나은 성능을 가진 학습 모델을 만들려면?
종속변수를 설명하는데 도움이 되는 독립변수가 여러 개일 때
-모든 독립변수가 종속변수를 설명하는데 동일하게 기여하는가?
-기여도가 높은 독립변수와 기여도가 낮은 독립변수를 구분
-기여도가 낮거나 거의 없는 변수들은 학습 모형에서 제외시킴
설명변수의 숫자가 많은수록 좋은 학습 모델이라 할 수 있는가?
-설명변수의 숫자가 적을수록 좋은 학습 모델이라 할 수 있음
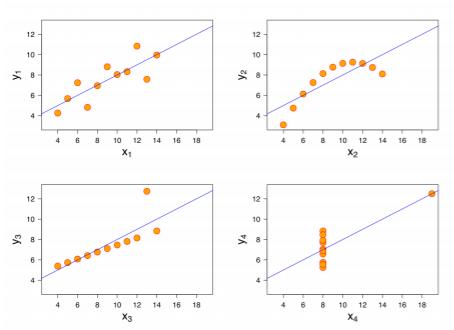
앤스컴의 4중주:Anscombe's Quartet
기술통계량은 그래프보다 데이터를 더 잘 설명할 수 있는가?