다익스트라 알고리즘(Dijkstra's Algorithm)

📌 다익스트라 알고리즘(Dijkstra's Algorithm)

그래프의 한 정점에서 모든 정점까지의 최단거리를 각각 구하는 알고리즘(최단 경로 문제, Shortest Path Problem)이다.

다익스트라 최단 경로 알고리즘의 줄임말
가장 유명하고 널리 사용되는 알고리즘 중 하나이다.

• 그래프에 대해 작동한다.
• 코딩을 할 때 우선순위 큐를 사용한다.
• 우선순위 큐 대신 이진 힙을 사용하면 더 빠르다.

활용

• GPS : 최단 경로 찾을 때 사용
• 네트워크 라우팅
• 생물학 : 전염병 퍼지는 것을 예측할 때 사용

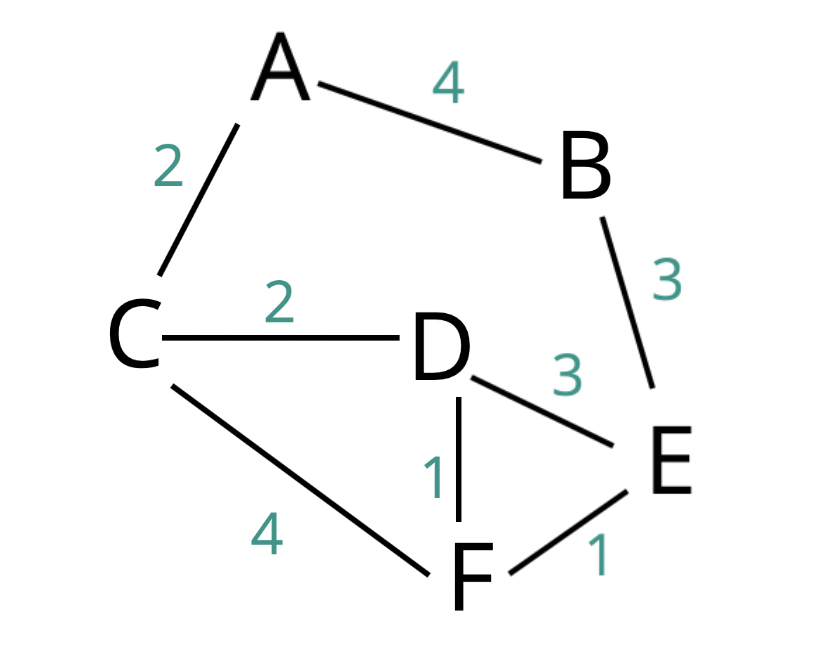
가중 그래프 만들기

다익스트라 알고리즘을 적용할 가중 그래프를 만들어보자.
일반 그래프에서는 연결되는 노드만 작성해주었지만, 가중 그래프에서는 다음과 같이 가중치도 적어준다.

{
	A : [{ node : B, weight : 4}, { node : C, weight : 2}]
    B : [{ node : A, weight : 4}, { node : E, weight : 3}]
}

class WeightedGraph {
    constructor() {
        this.adjacencyList = {};
    }
    addVertex(vertex){
        if(!this.adjacencyList[vertex]) this.adjacencyList[vertex] = [];
    }
    addEdge(vertex1,vertex2, weight){
        this.adjacencyList[vertex1].push({node:vertex2,weight});
        this.adjacencyList[vertex2].push({node:vertex1, weight});
    }
}

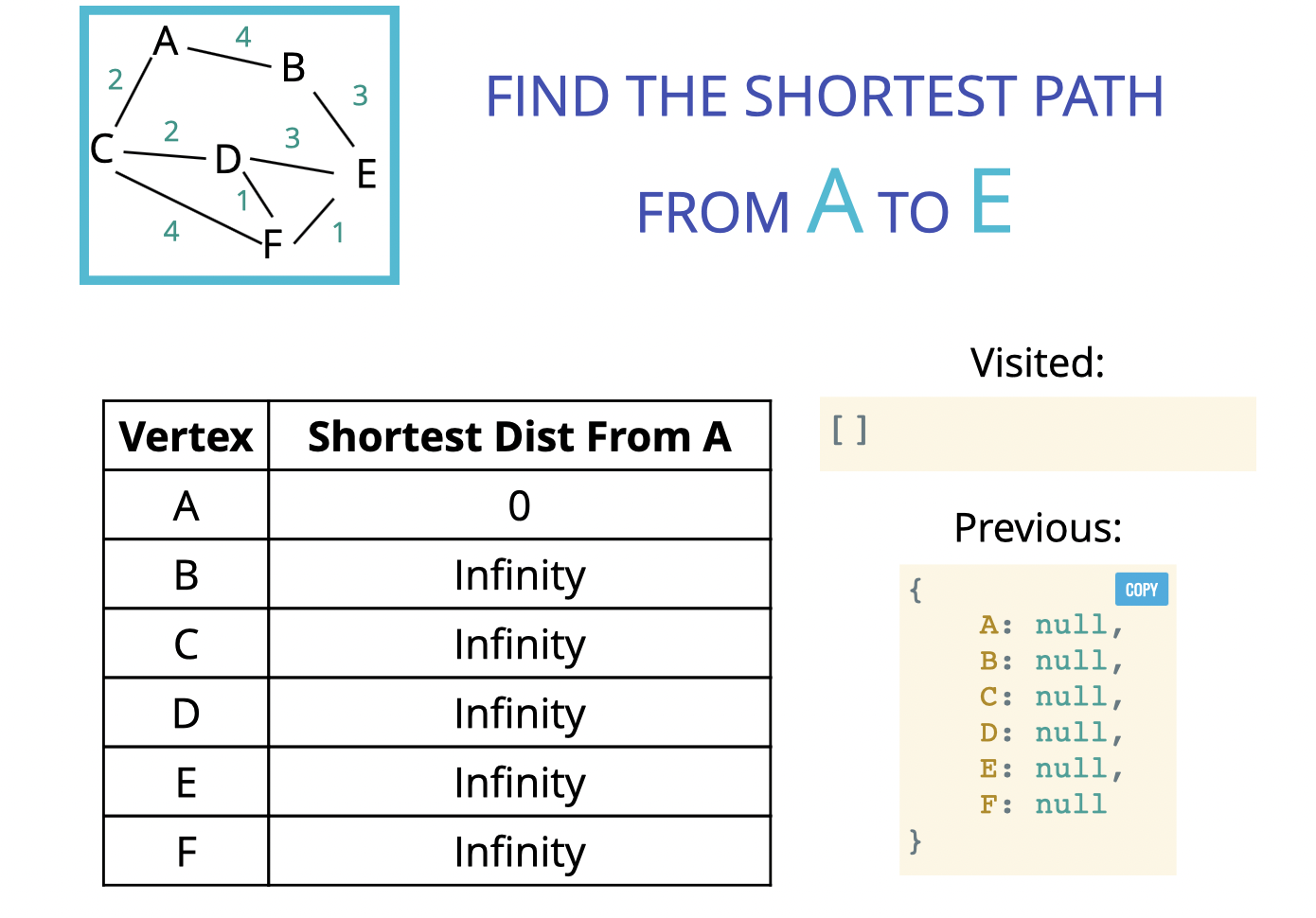
각 노드에서 최단 거리 구하기

1. 초기값 세팅(0 혹은 Infinity)
   출발점은 본인에 대한 거리가 0이므로 0으로 초기화, 나머지는 거리가 어떻게 되는지 모르므로 Infinity로 초기화한다.
   
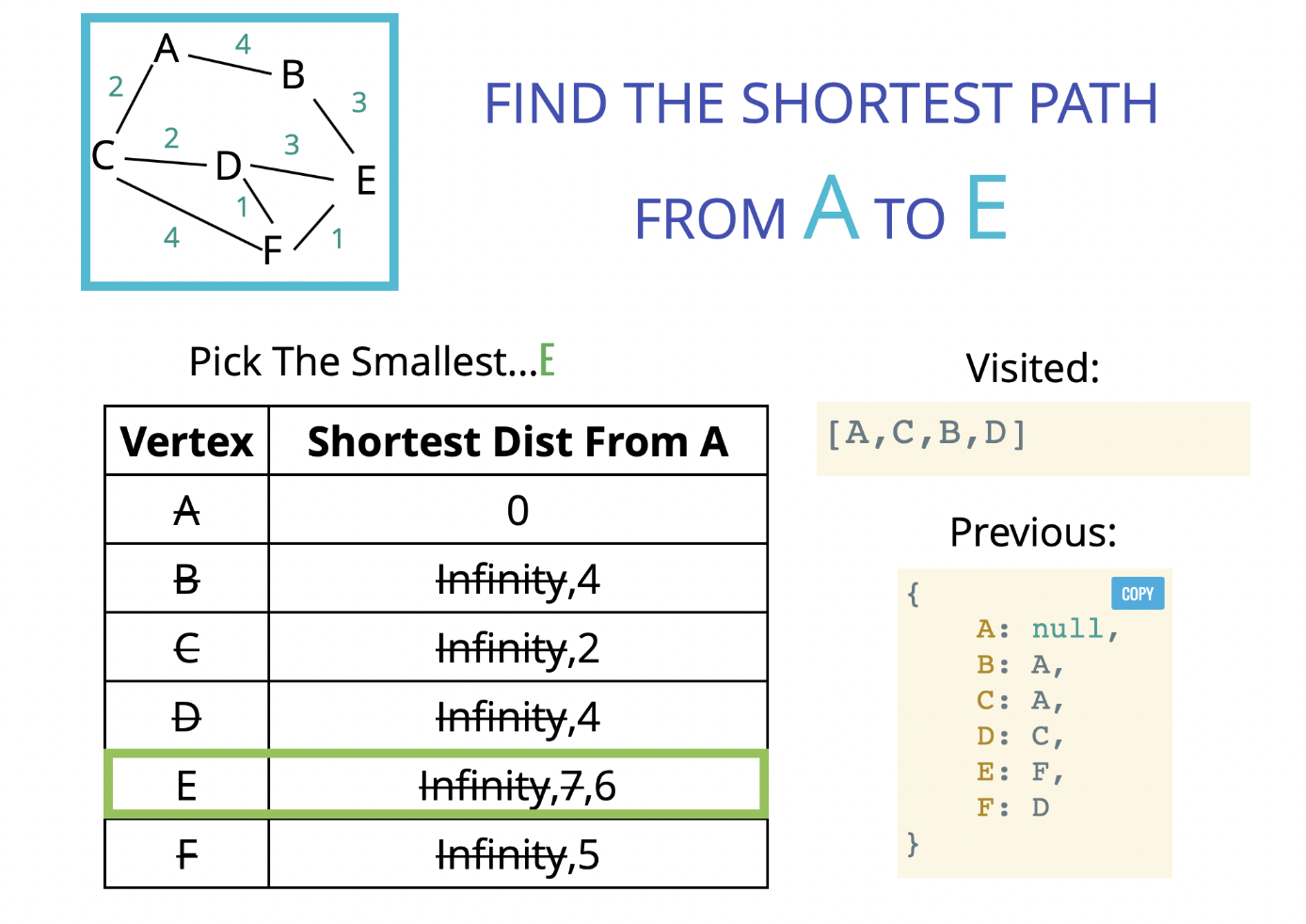
2. 출발점과 인접한 노드와의 거리를 구한다.

• B에서 A의 거리 : 4, C에서 A의 거리 : 2
• D에서 A의 거리 : 4 (D-C-A), F에서 A의 거리 : 5(F-D-C-A)
• 더 짧은 거리가 있으면 업데이트

3. 어디에서 왔는지 기록한다.(previous)
   D는 C에서 왔고, C는 A에서 왔다. (A-C-D)
   

우선순위 큐

값과 우선순위를 입력하면 우선순위가 높은 것이 먼저 실행되도록 정렬해준다.

class PriorityQueue {
  constructor(){
    this.values = [];
  }
  enqueue(val, priority) {
    this.values.push({val, priority});
    this.sort();
  };
  dequeue() {
    return this.values.shift();
  };
  sort() {
    this.values.sort((a, b) => a.priority - b.priority);
  };
}

다익스트라 알고리즘 구현

class WeightedGraph {
    constructor() {
        this.adjacencyList = {};
    }
    addVertex(vertex){
        if(!this.adjacencyList[vertex]) this.adjacencyList[vertex] = [];
    }
    addEdge(vertex1,vertex2, weight){
        this.adjacencyList[vertex1].push({node:vertex2,weight});
        this.adjacencyList[vertex2].push({node:vertex1, weight});
    }
    Dijkstra(start, finish){
        const nodes = new PriorityQueue();
        const distances = {};
        const previous = {};
        let path = [] //to return at end
        let smallest;
        //build up initial state
        for(let vertex in this.adjacencyList){
            if(vertex === start){
                distances[vertex] = 0;
                nodes.enqueue(vertex, 0);
            } else {
                distances[vertex] = Infinity;
                nodes.enqueue(vertex, Infinity);
            }
            previous[vertex] = null;
        }
        // as long as there is something to visit
        while(nodes.values.length){
            smallest = nodes.dequeue().val;
            if(smallest === finish){
                //WE ARE DONE
                //BUILD UP PATH TO RETURN AT END
                while(previous[smallest]){
                    path.push(smallest);
                    smallest = previous[smallest];
                }
                break;
            } 
            if(smallest || distances[smallest] !== Infinity){
                for(let neighbor in this.adjacencyList[smallest]){
                    //find neighboring node
                    let nextNode = this.adjacencyList[smallest][neighbor];
                    //calculate new distance to neighboring node
                    let candidate = distances[smallest] + nextNode.weight;
                    let nextNeighbor = nextNode.node;
                    if(candidate < distances[nextNeighbor]){
                        //updating new smallest distance to neighbor
                        distances[nextNeighbor] = candidate;
                        //updating previous - How we got to neighbor
                        previous[nextNeighbor] = smallest;
                        //enqueue in priority queue with new priority
                        nodes.enqueue(nextNeighbor, candidate);
                    }
                }
            }
        }
        return path.concat(smallest).reverse();     
    }
}

class PriorityQueue {
    constructor(){
        this.values = [];
    }
    enqueue(val, priority){
        let newNode = new Node(val, priority);
        this.values.push(newNode);
        this.bubbleUp();
    }
    bubbleUp(){
        let idx = this.values.length - 1;
        const element = this.values[idx];
        while(idx > 0){
            let parentIdx = Math.floor((idx - 1)/2);
            let parent = this.values[parentIdx];
            if(element.priority >= parent.priority) break;
            this.values[parentIdx] = element;
            this.values[idx] = parent;
            idx = parentIdx;
        }
    }
    dequeue(){
        const min = this.values[0];
        const end = this.values.pop();
        if(this.values.length > 0){
            this.values[0] = end;
            this.sinkDown();
        }
        return min;
    }
    sinkDown(){
        let idx = 0;
        const length = this.values.length;
        const element = this.values[0];
        while(true){
            let leftChildIdx = 2 * idx + 1;
            let rightChildIdx = 2 * idx + 2;
            let leftChild,rightChild;
            let swap = null;

            if(leftChildIdx < length){
                leftChild = this.values[leftChildIdx];
                if(leftChild.priority < element.priority) {
                    swap = leftChildIdx;
                }
            }
            if(rightChildIdx < length){
                rightChild = this.values[rightChildIdx];
                if(
                    (swap === null && rightChild.priority < element.priority) || 
                    (swap !== null && rightChild.priority < leftChild.priority)
                ) {
                   swap = rightChildIdx;
                }
            }
            if(swap === null) break;
            this.values[idx] = this.values[swap];
            this.values[swap] = element;
            idx = swap;
        }
    }
}

class Node {
    constructor(val, priority){
        this.val = val;
        this.priority = priority;
    }
}

var graph = new WeightedGraph()
graph.addVertex("A");
graph.addVertex("B");
graph.addVertex("C");
graph.addVertex("D");
graph.addVertex("E");
graph.addVertex("F");

graph.addEdge("A","B", 4);
graph.addEdge("A","C", 2);
graph.addEdge("B","E", 3);
graph.addEdge("C","D", 2);
graph.addEdge("C","F", 4);
graph.addEdge("D","E", 3);
graph.addEdge("D","F", 1);
graph.addEdge("E","F", 1);


graph.Dijkstra("A", "E");