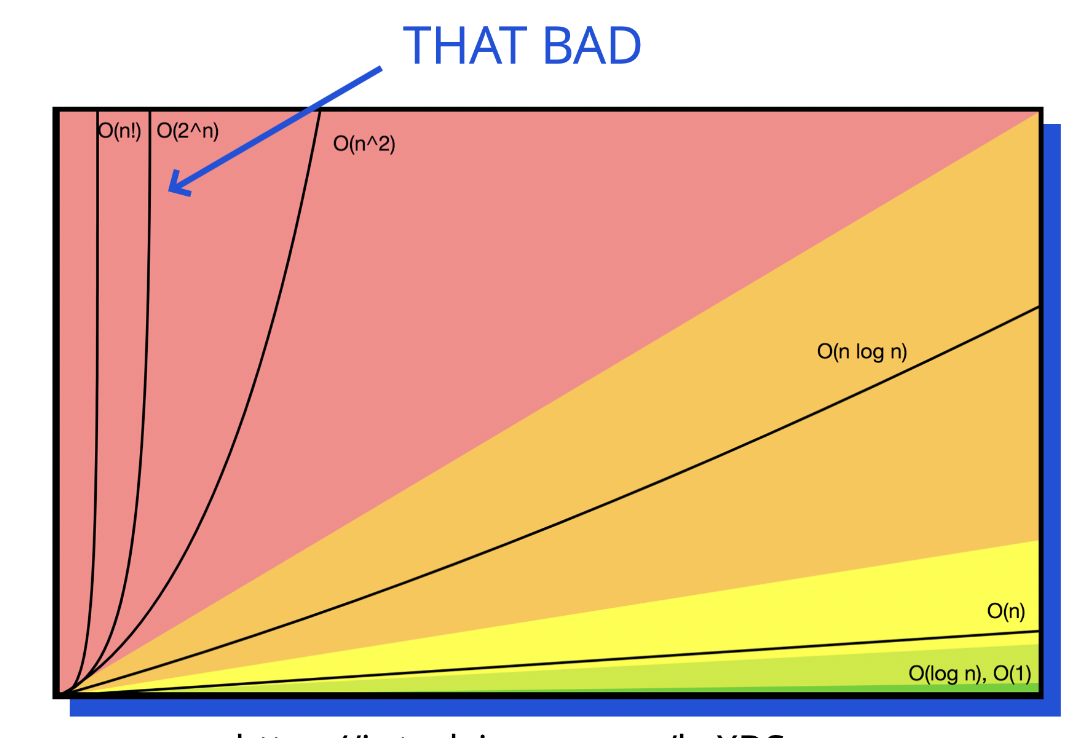
📌 동적 프로그래밍(Dynamic Programming, DP)
복잡한 문제를 더 간단한 하위 문제의 모음으로 쪼개서 푸는 프로그래밍 방식을 뜻한다.
DP 종류
Memoization: 하향식 접근Tabulation: 상향식 접근
동적 프로그래밍을 효율적으로 사용할 수 있는 문제 조건
1. 반복되는 하위 문제
: 동적 프로그래밍을 쓰기 위해서는 그 문제에 중첩되는 하위 문제가 있어야 한다.
(문제를 더 작은 문제로 쪼개고 그 문제가 재활용될 수 있는 형태.)
ex. 피보나치 수열
2. 최적 부분 구조
: 하위 문제의 최적 해답을 통해서 더 큰 범주의 문제의 최적 해답을 구할 수 있는 경우
ex. 피보나치 수열, 최단경로
예시 ) 피보나치 수열

기본적인 재귀를 이용한 풀이
function fib(n){
if(n <= 2) return 1;
return fib(n-1) + fib(n-2);
}시간 복잡도 : O(2^n) 으로, 매우 안좋다.
- 입력값이 100 정도만 넘어가도 stack overflow 발생.
DP 방식 1 ) Memoization
반복적으로 계산되는 것들의 계산 횟수를 줄이기 위해 이전에 계산했던 값을 저장해두었다가 나중에 재사용하는 방법. (하향식 접근)
- 값을 담을 배열을 추가한다.
- 배열에 값이 이미 있으면 새로 계산하지 않고 있는 값을 꺼내쓴다.
- 배열에 값이 없으면 이전 값을 이용해 계산해서 배열에 추가하고 반환한다.
function fib(n, memo = [undefined,1,1]){
if(memo[n] !== undefined) return memo[n];
var res = fib(n-1, memo) + fib(n-2, memo);
memo[n] = res;
return res;
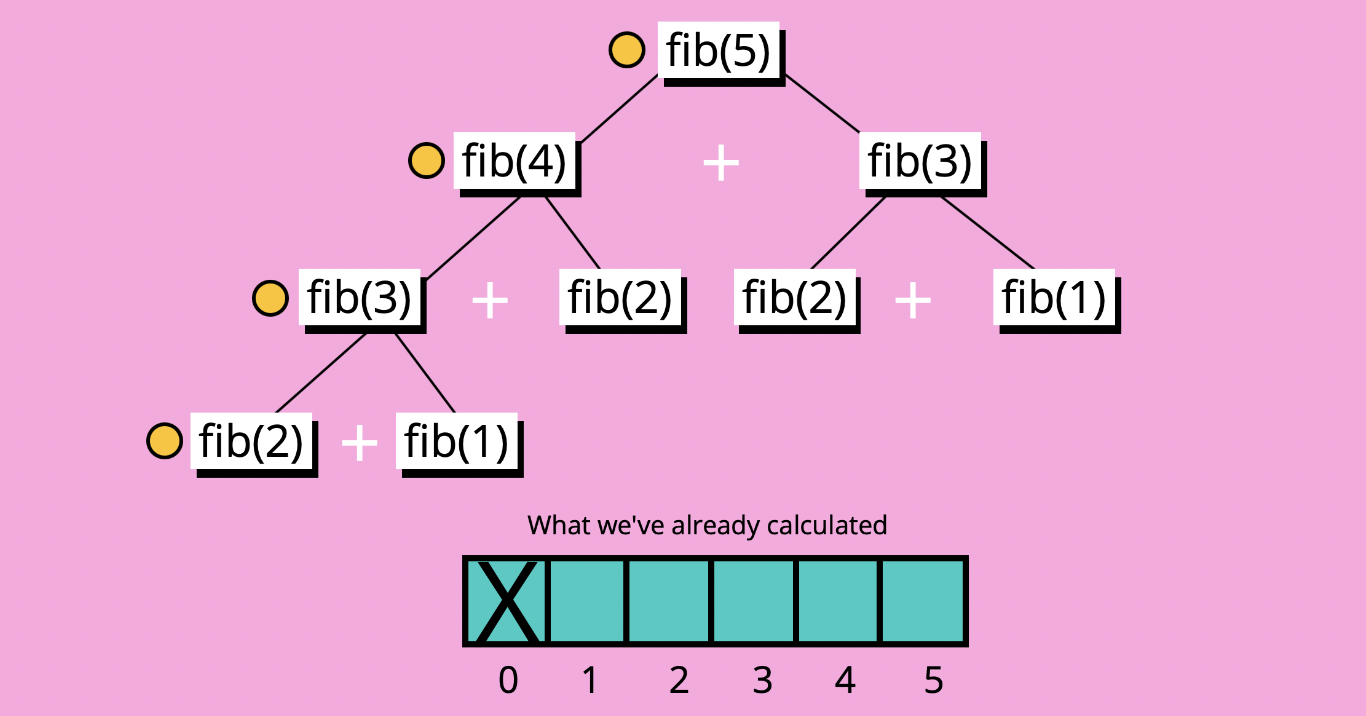
}ex. fib(5)
fib(3),fib(4),fib(5)를 순서대로 구해서 배열에 담는다.
(fib(1),fib(2)는 배열에 초기값으로 미리 넣어두었으므로 패스한다.)
- 오른쪽에 있는
fib(3)를 구할 때에는fib(1) + fib(2)를 다시 계산하지 않고, 기존에 있는fib(3)를 배열에서 가져와 쓴다. - 이런 방식으로 반복되는 연산을 줄이다 보면 입력값이 커져도 시간을 많이 단축시킬 수 있다.
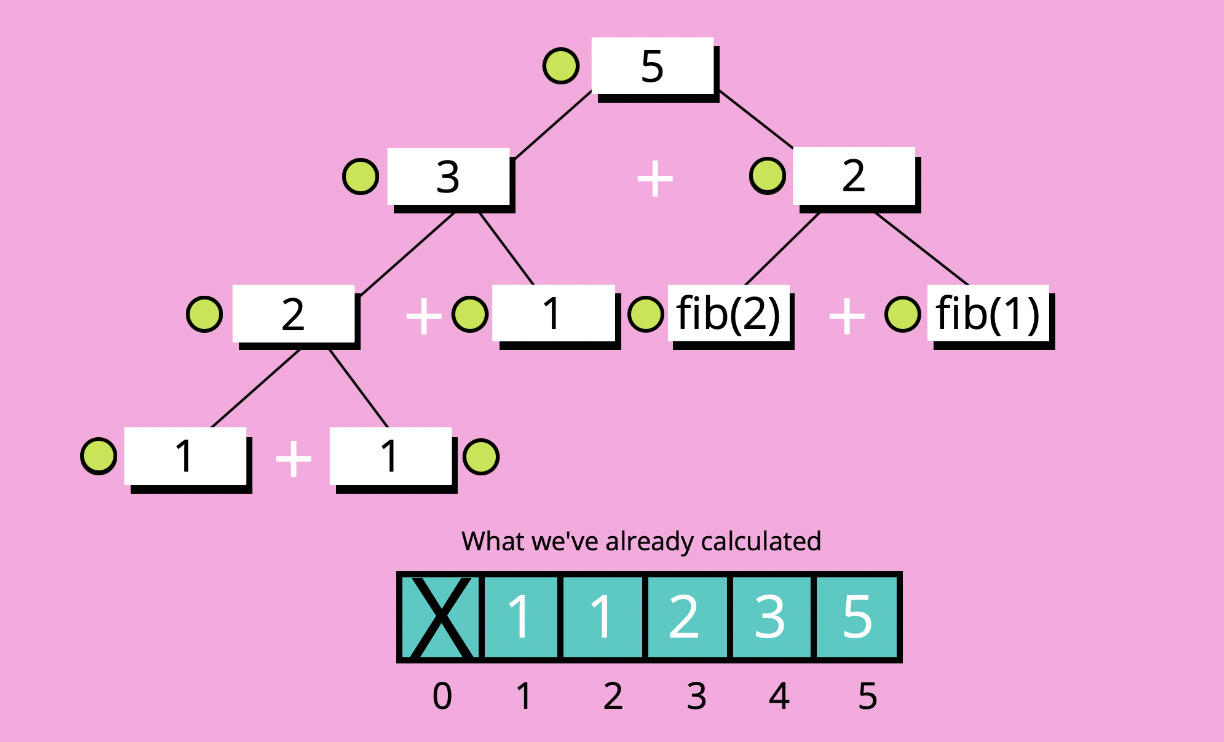
시간 복잡도 : O(n)으로 개선
DP 방식 2 ) Tabulation
가장 작은 하위 문제를 풀어 테이블(배열, 객체 등)에 저장하고, 루프를 사용해 값을 상향식으로 구해나간다. (상향식 접근)
- 초기값을 배열에 담아둔다.
- 이전 값을 이용해 n까지의 피보나치 수열을 완성한다.
function fib(n){
if(n <= 2) return 1;
var fibNums = [undefined, 1, 1];
for(let i=3; i<=n; i++){
fibNums[i] = fibNums[i-1] + fibNums[i-2];
}
return fibNums[n];
}ex. fib(6)
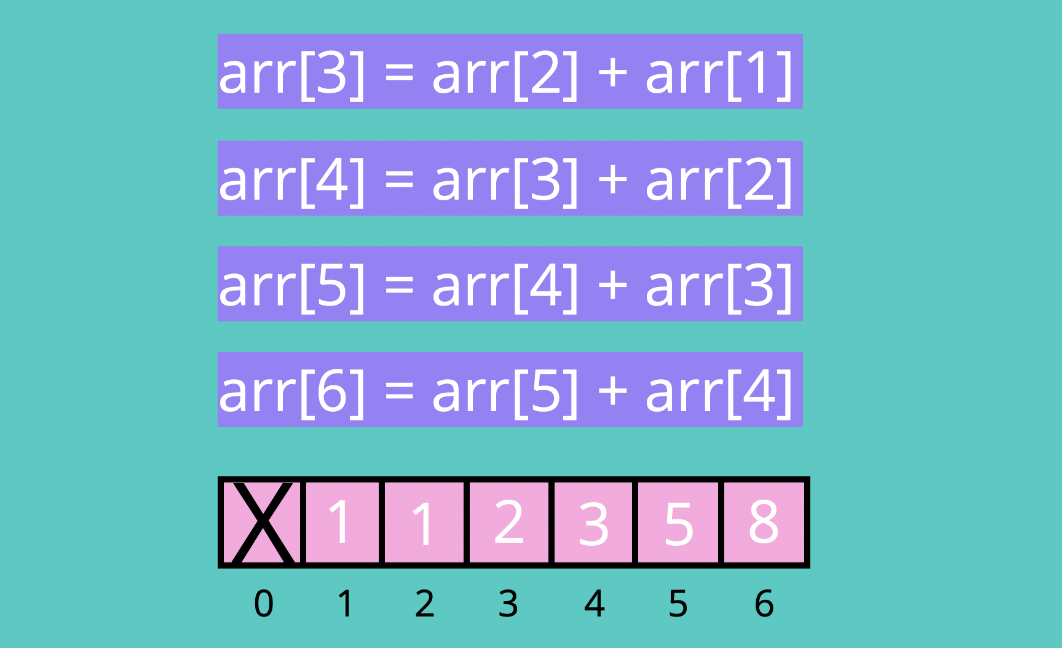
시간 복잡도는 두 방식 모두 O(n)이지만, 공간 복잡도는
Tabulation방식이 더 좋다.
- 입력값을 매우 크게 넣으면
Memoization방식에서는stack overflow가 발생하지만,Tabulation방식에서는stack overflow가 발생하지 않는다.
(다만, 자바스크립트 정수 범위를 넘어가면Infinity로 표현된다.)Memoization에서는 재귀를 사용했기 때문에 스택에서 대기하고 있는 해결되지 않은 재귀 호출들이 많다. 그러나,Tabulation에서는 재귀를 사용하지 않아 공간 복잡도가 더 낮다.
참고 https://www.zerocho.com/category/Algorithm/post/584b979a580277001862f182