머신러닝이란?
머신러닝의 목표

머신러닝은 input (X)로부터 ouput (Y)를 추출하도록 하는 f(x)를 찾는 과정이다. 정확한 함수를 찾는다기보다는 충분히 근사치를 도출하는 함수를 찾는 것이 머신러닝의 목표이다.
학습의 종류
학습의 종류에는 크게 네 가지가 있다. 적절한 f(x)를 찾기 위해 다음과 같은 방법 중에 택하여 학습할 수 있다. 머신러닝에서는 다음의 학습 방법 중에 상황에 맞는 학습 방법을 택하여 학습을 한다.
1. Supervised Learning (지도학습)
지도학습이란 Training Dataset에 x와 함께 Label 즉, y가 주어지는 경우이다. 학습 데이터 안에 정답을 함께 제공하는 것이다.
2. Unsupervised Learning (비지도학습)
비지도학습에서는 지도학습과는 반대로 y 없이 x만 주어진다.
3. Weekly / Semi-supervised Learning (반지도학습)
반지도학습에서는 일부 Training Dataset에는 x와 함께 y가 주어지고, 일부 Training Dataset에는 y 없이 x만 주어진다.
4. Reinforcement Learning (강화학습)
강화학습이란 action에 따른 reward(보상)을 주면서 계속 훈련시키는 것을 말한다.
Linear Regression (선형회귀)
Linear Method
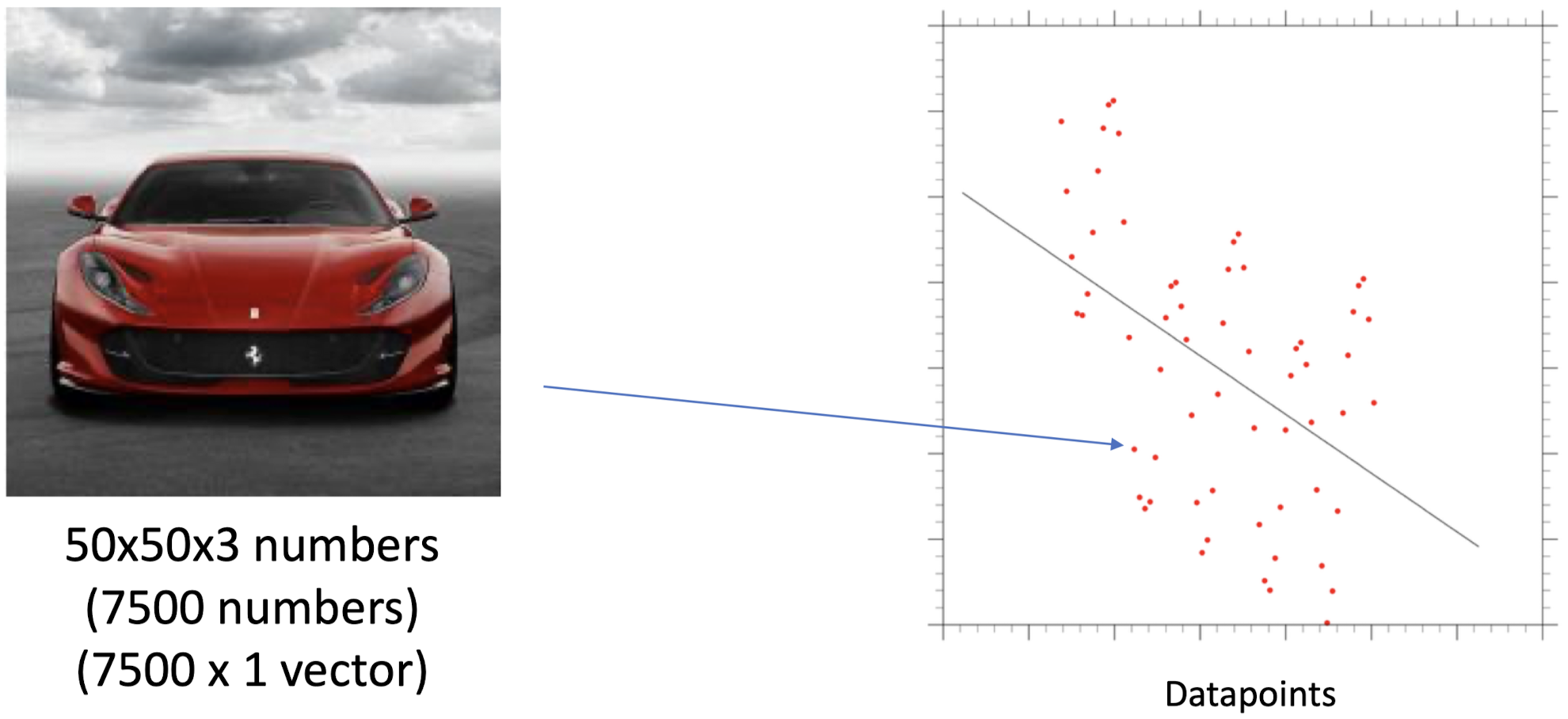
위의 그림처럼 데이터를 2차원 평면 위의 점들의 집합으로 옮긴 뒤, 그 점들을 가장 잘 대표할 수 있는 적절한 f(x)를 구하기 위해서는 어떻게 해야 할까? 그 방법 중 하나로 Linear Method가 있다. f(x) = wx + b 의 형태로 설정하고 가장 적절한 w값과 b값을 찾는 방법이다. 이때 w는 slope(경사), b는 bias(편향)으로 부른다.
Regression vs Classification
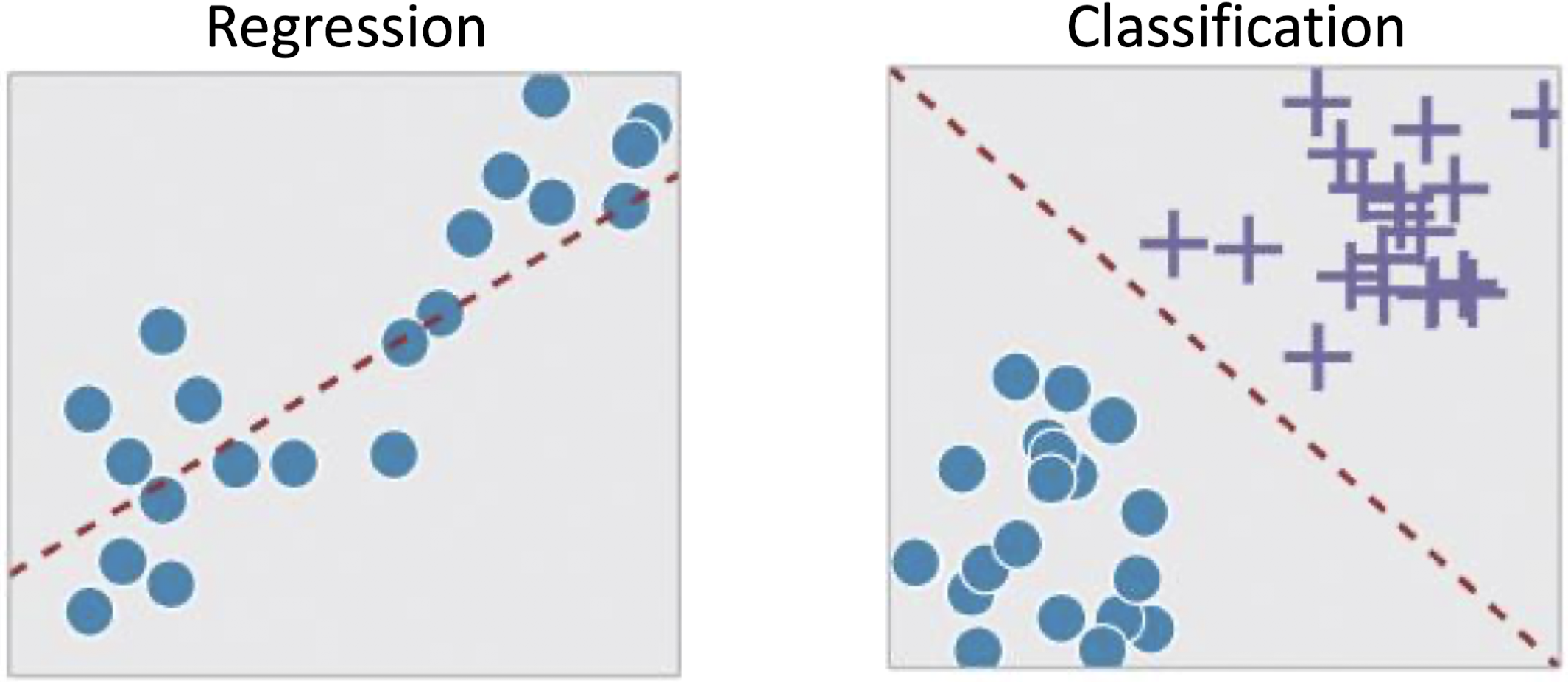
Regression은 데이터의 경향성을 가장 잘 나타낼 수 있는 선을 찾는 행위이며, 데이터의 패턴을 분석할 때 주로 사용한다. 이와 달리 Classification은 데이터를 분류할 수 있는 구분선을 찾는 행위이며, 클래스를 나눌 때 주로 사용한다.
Linear Regression
본론으로 돌아와서, Linear Method와 Regression에 대한 이해를 바탕으로, Linear Regression(선형회귀)은 선형의 경향성을 가장 잘 나타내는 선을 찾는 행위임을 알 수 있다.
선형회귀가 사용되는 경우는 정말 많은데, 주로 두 변수의 관계를 분석하는 경우에 주로 사용된다. 예를 들어, 부모와 키와 자식의 키의 관계를 예측하는 것이나 기업의 순이익과 주가와의 관계를 분석하는 경우 등에서 선형회귀가 사용된다.
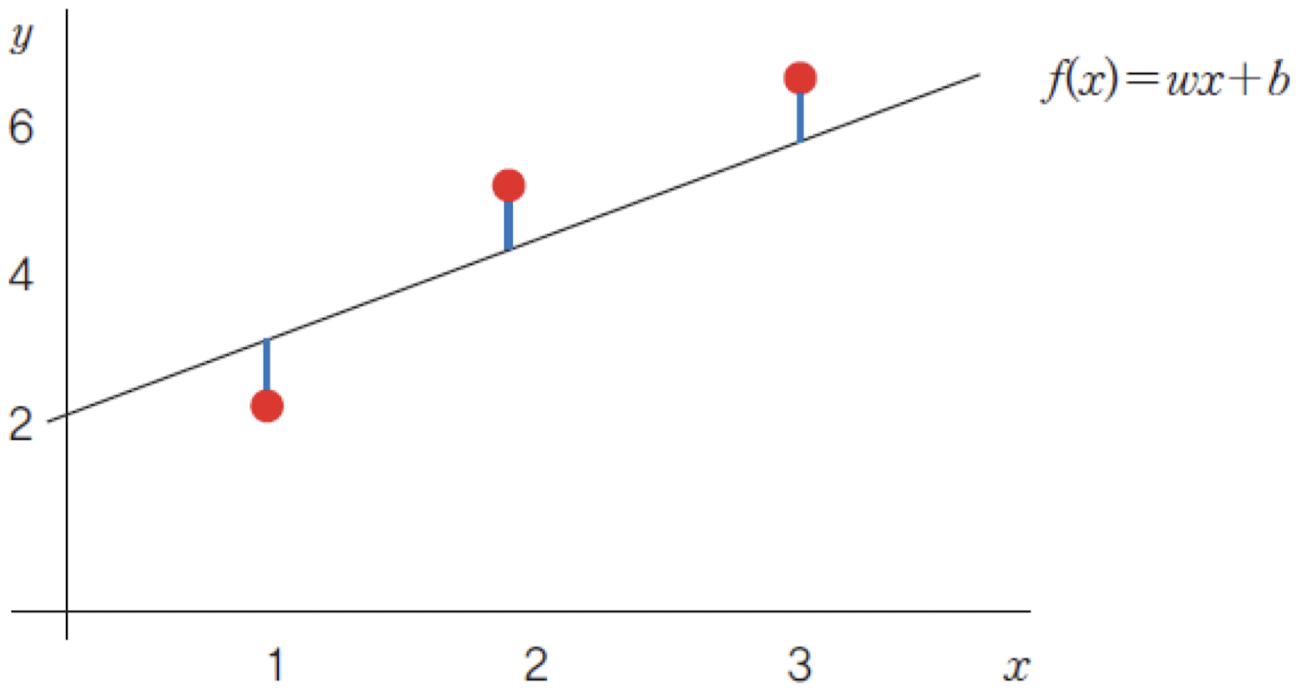
위의 그림과 같이 세 개의 점이 주어져있다고 하자. 선형회귀에서는 파란색으로 표시된 오차의 제곱의 합을 최소로 하는 f(x)를 찾는 것을 목표로 한다. 이때, 오차의 제곱인 (y - f(x))^2 의 총합을 일반화한 식은 다음과 같다.
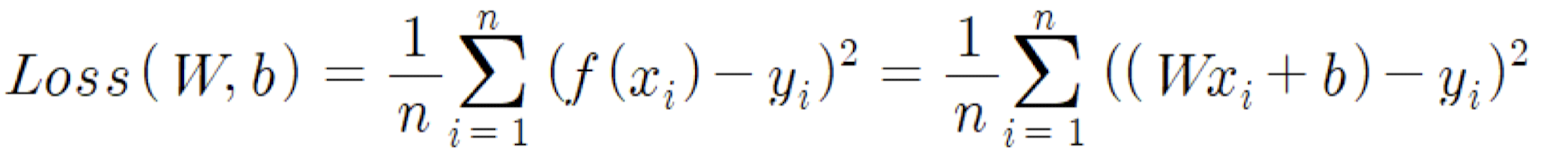
이 Loss를 최소로 만드는 W값과 b값을 구하기 위한 방법이 바로 Gradient Descent(경사하강법)이다.
Gradient Descent (경사하강법)

경사하강법은 반복을 통한 최적화 알고리즘이다. 미분값에 반대 부호를 붙여 기울기의 반대 방향으로 이동함으로써 기울기가 0인 지점으로 수렴하는 것이 목적인 알고리즘이다. 이때 γ_w와 γ_b는 Learning Rate이라고 한다.
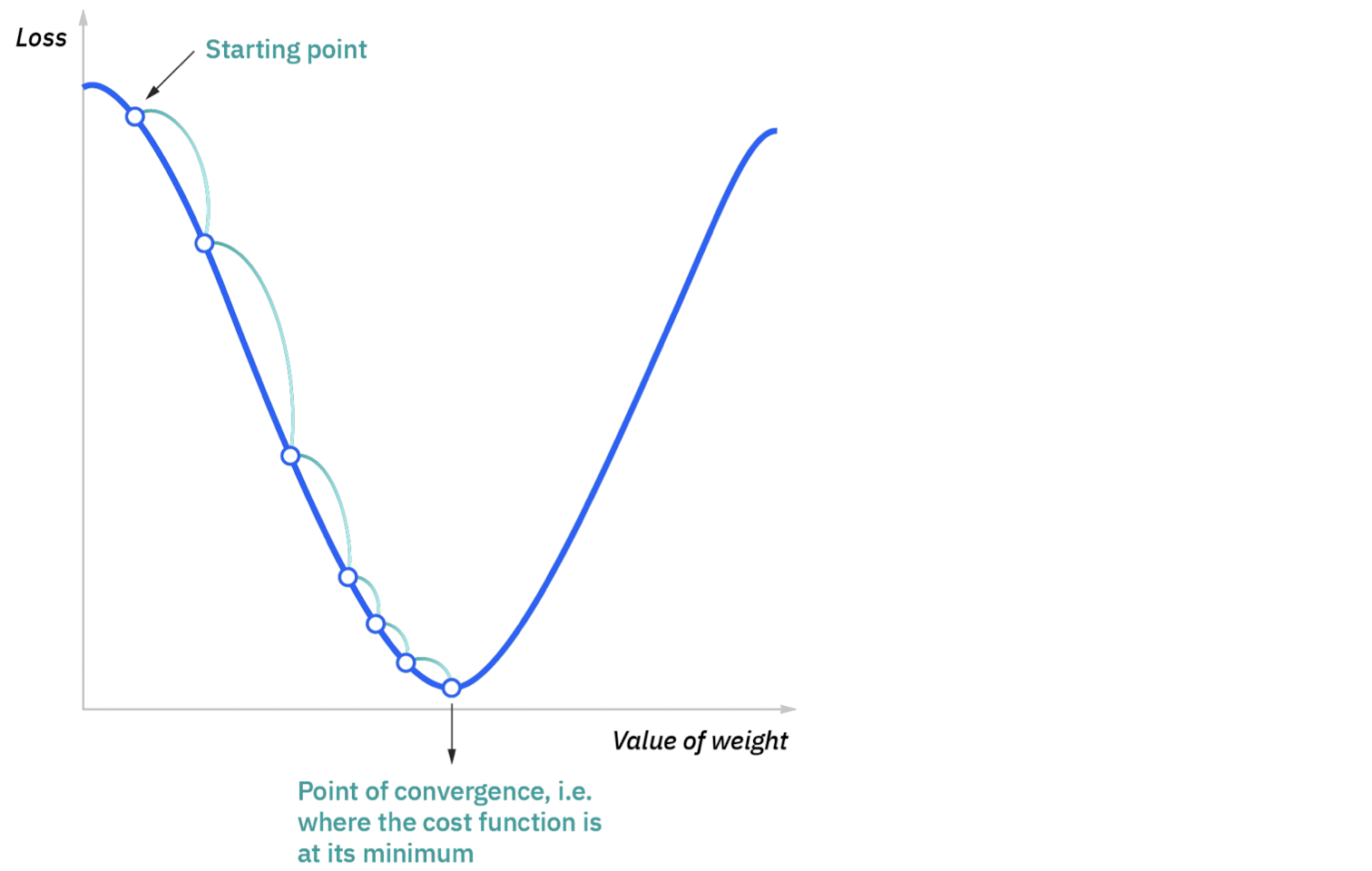
위의 그림에서 확인할 수 있다시피, Starting point에서 출발하여 기울기의 반대방향으로 계속 이동하다보면 언젠가는 기울기가 0인 지점에 수렴한다는 것이 경사하강법의 아이디어이다.
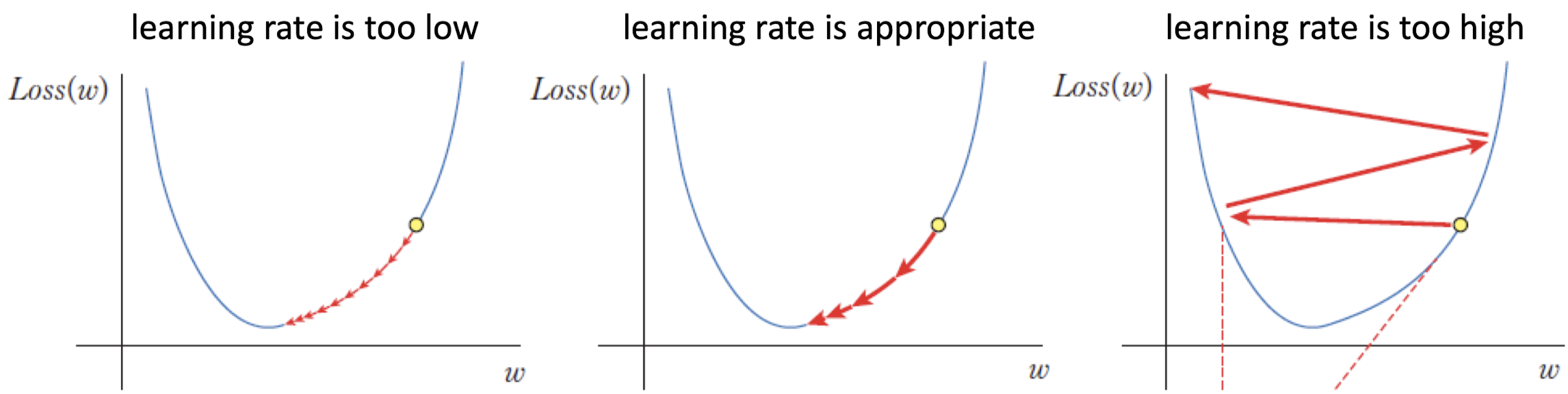
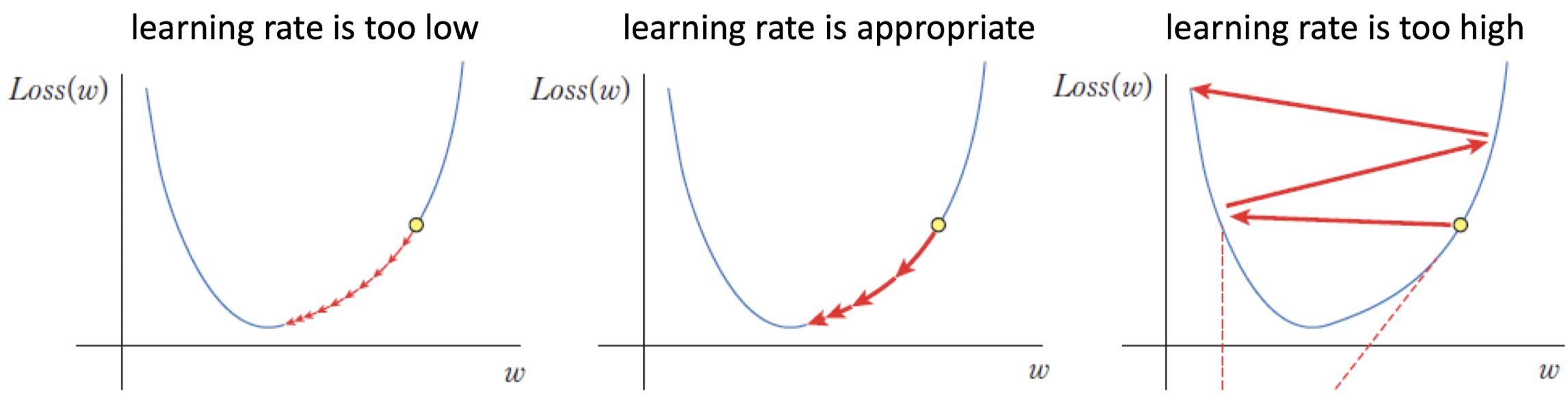
Learning Rate는 Hyper Paramenter로서, 우리가 직접 튜닝해줘야 하는 파라미터이다. Learning Rate가 너무 작으면 최저점을 찾는데 너무 오래 걸리고, Learning Rate가 너무 크면 최저점으로 수렴하지 못하고 발산할 수 있기 때문에 적절한 Learning Rate를 설정하는 것이 결과에 지대한 영향을 준다고 한다.
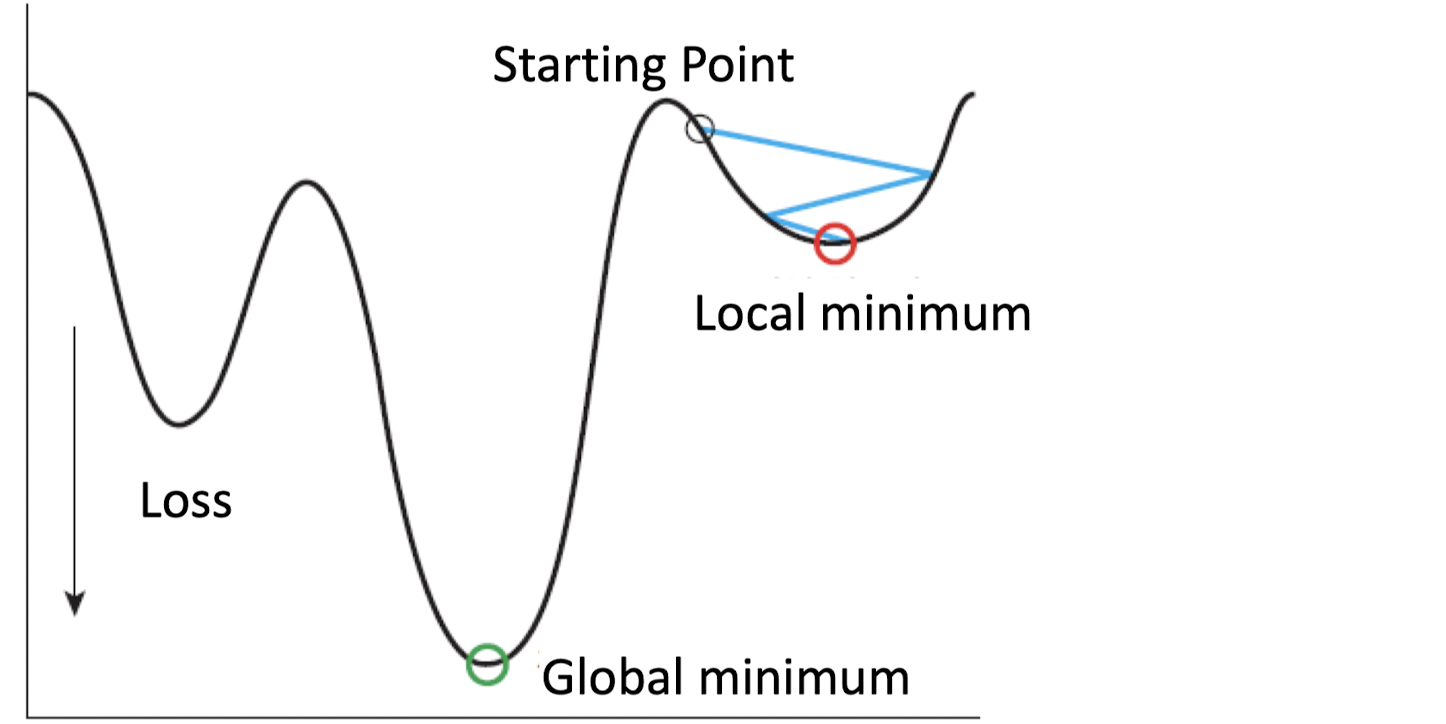
이러한 경사하강법은 Global minimun에 도달하지 못한 채 Local minimun에 수렴해 갇혀버리는 경우가 대부분인데, 이것만으로도 충분히 유의미한 결과를 도출할 수 있다고 한다.
