기계학습심화 - 2. GD, SGD, Traditional Classification Method (KNN)

현종혁·2024년 4월 16일

AI Gradient Descent K-Nearest Neighbors KNN SGD gd stochastic gradient descent 경사하강법 기계학습 딥러닝 머신러닝 확률적 경사하강법

기계학습심화

목록 보기

3/8

Gradient Descent (경사하강법)

경사하강법을 다차원으로 확장

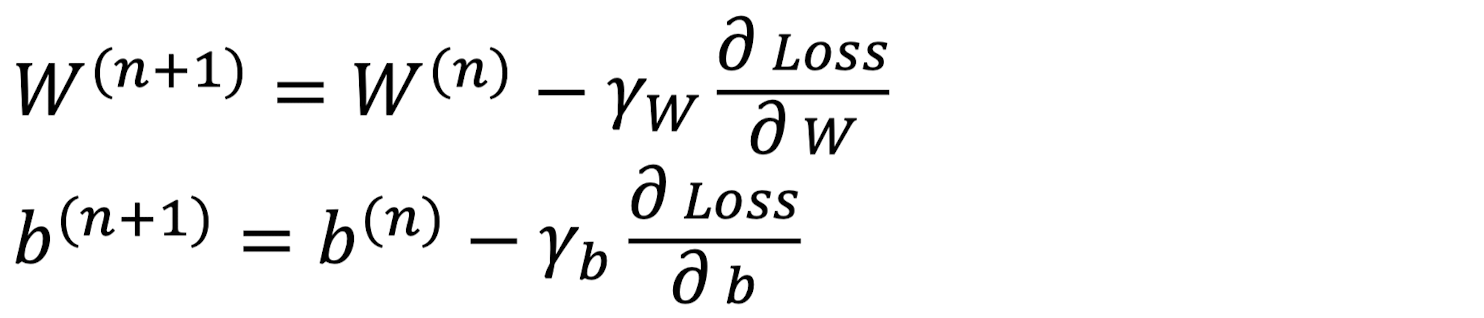
지난 1번 글에서 학습한 위의 W, b에 대한 경사하강법 수식을 행렬 수식으로 표현하면 다음과 같다.

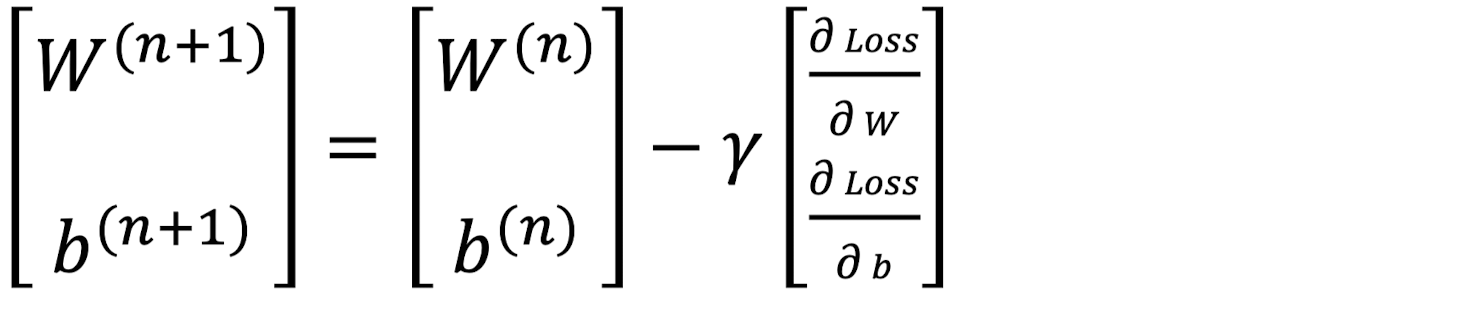
이때, 마지막 항에서 Learning Rate γ를 제외한 부분이 Loss의 변화량을 벡터로 모아놓은 것이 된다.

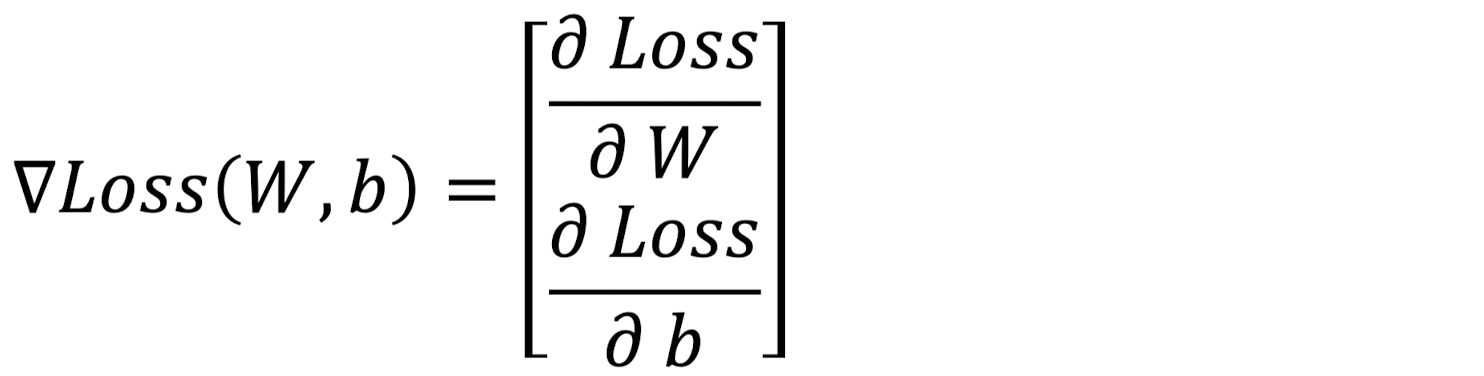
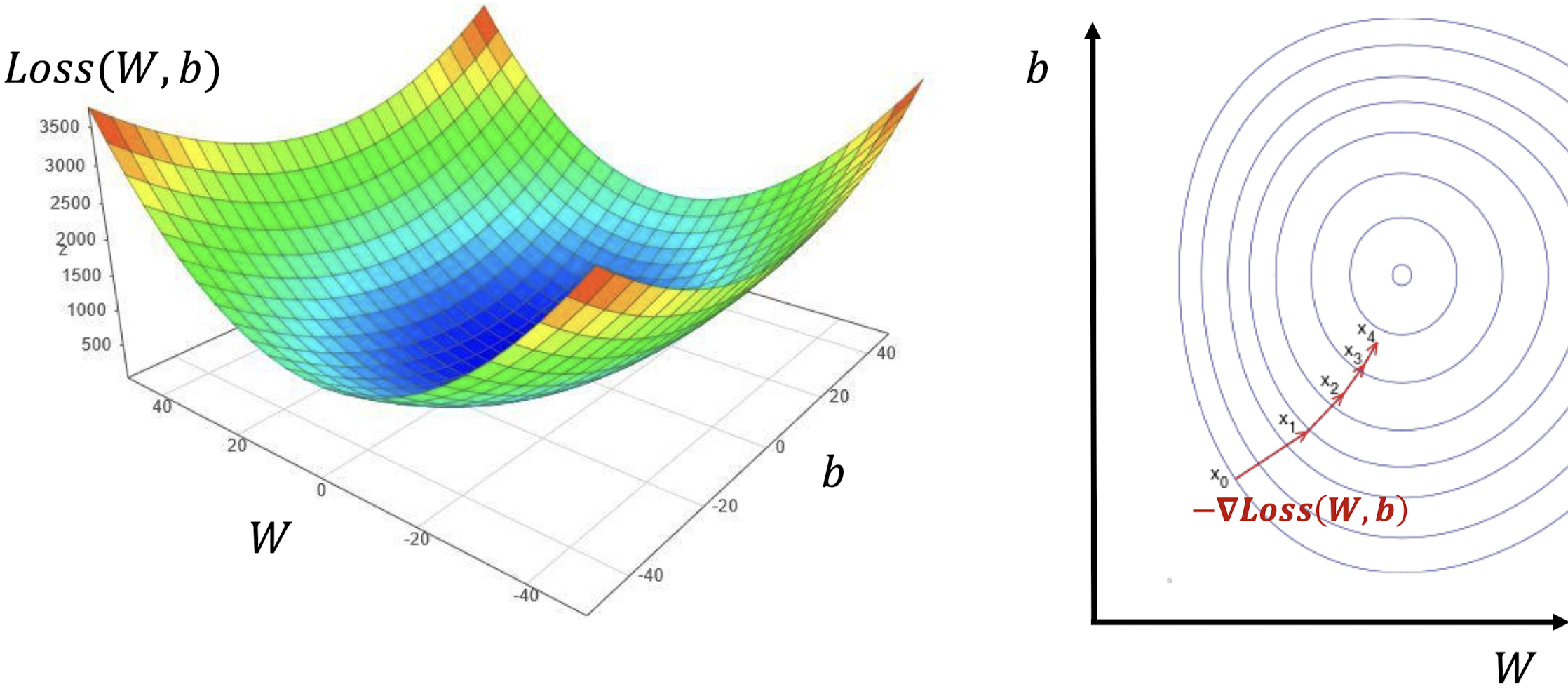
이제 W, b, Loss(W, b)를 세 축으로 하는 3차원 공간 위에 올려보자. (왼쪽 그림)
그리고 W, b를 두 축으로 하는 2차원 평면 위에 Loss를 미분한 값에에 - 부호를 붙여서 벡터로 나타내면 다음과 같다. (오른쪽 그림, -∇Loss(W, b) )

Stochastic Gradient Descent (확률적 경사하강법)

Stochastic Gradient Descent의 필요성

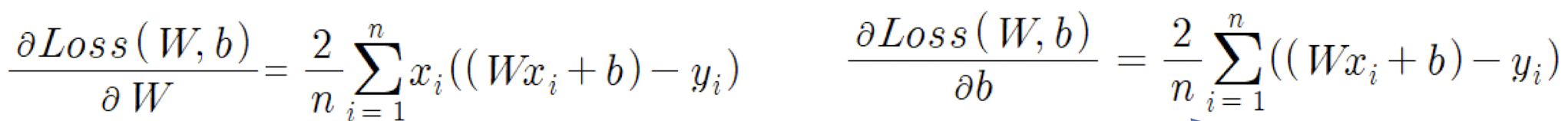
위의 수식들은 각각 Loss를 W, b에 대해 미분한 것이다. 기존의 경사하강법을 컴퓨터로 계산하면 모든 데이터셋에 대한 총합을 구하는 연산을 해야 되기 때문에 계산량이 너무 많아 시간과 메모리가 너무 많이 필요하다. 이에 따라 등장하게 된 것이 바로 Stochastic Gradient Descent(확률적 경사하강법)이다.

Stochastic Gradient Descent란?

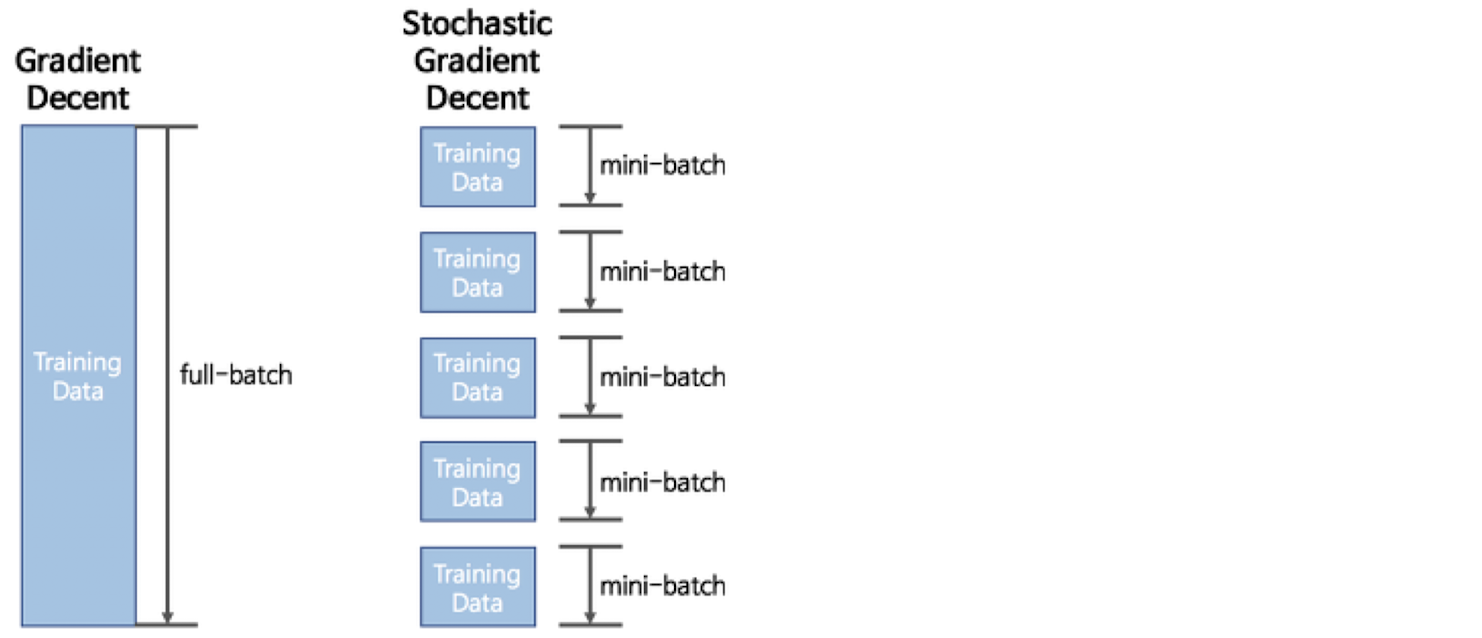
기존 Gradient Descent(이하 GD)가 전체 데이터셋을 대상으로 학습했다면, Stochastic Gradient Descent(이하 SGD)는 전체 데이터셋을 작은 데이터셋 여러 개로 쪼개서 학습한 뒤, 한 번의 학습이 끝날 때마다 W, b를 업데이트한다. 이때 전체 데이터셋을 full-batch, 쪼개진 데이터셋의 일부를 mini-batch라고 한다. SGD에서는 mini-batch 단위로 GD를 수행하며, 이를 계속 반복한다. 이때 각각의 수행을 epoch이라고 부른다.

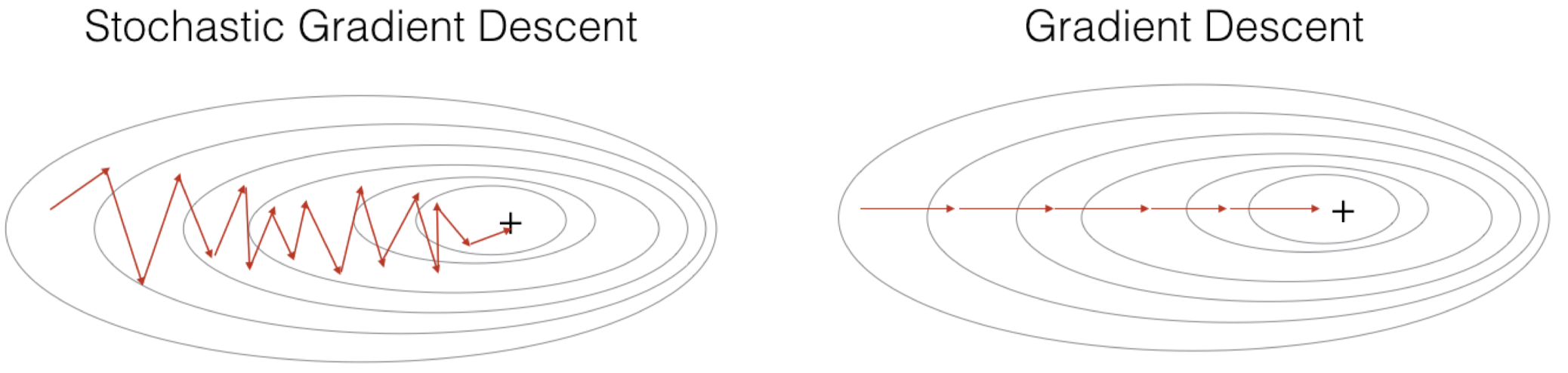
이러한 SGD의 단점으로는 왼쪽 그림과 같이 마지막에 한 값으로 수렴하지 못하고 Oscillation(진동)이 발생한다. 이에 대한 해결책으로 일반적인 GD에서는 Learning Rate를 바꾸지 않는 것과는 달리, SGD에서는 epoch마다 점점 Learning Rate을 줄여서 최대한 한 값으로 수렴할 수 있도록 한다.

GD, SGD는 모두 W와 b를 학습하기 위한 방법들이고, 이러한 방법들에는 ADAM, RMSPROP 등 여러가지 방법이 있다. 이들을 옵티마이저라고도 부른다.

Traditional Classification Method

KNN (K- Nearest Neighbor)

KNN이란?

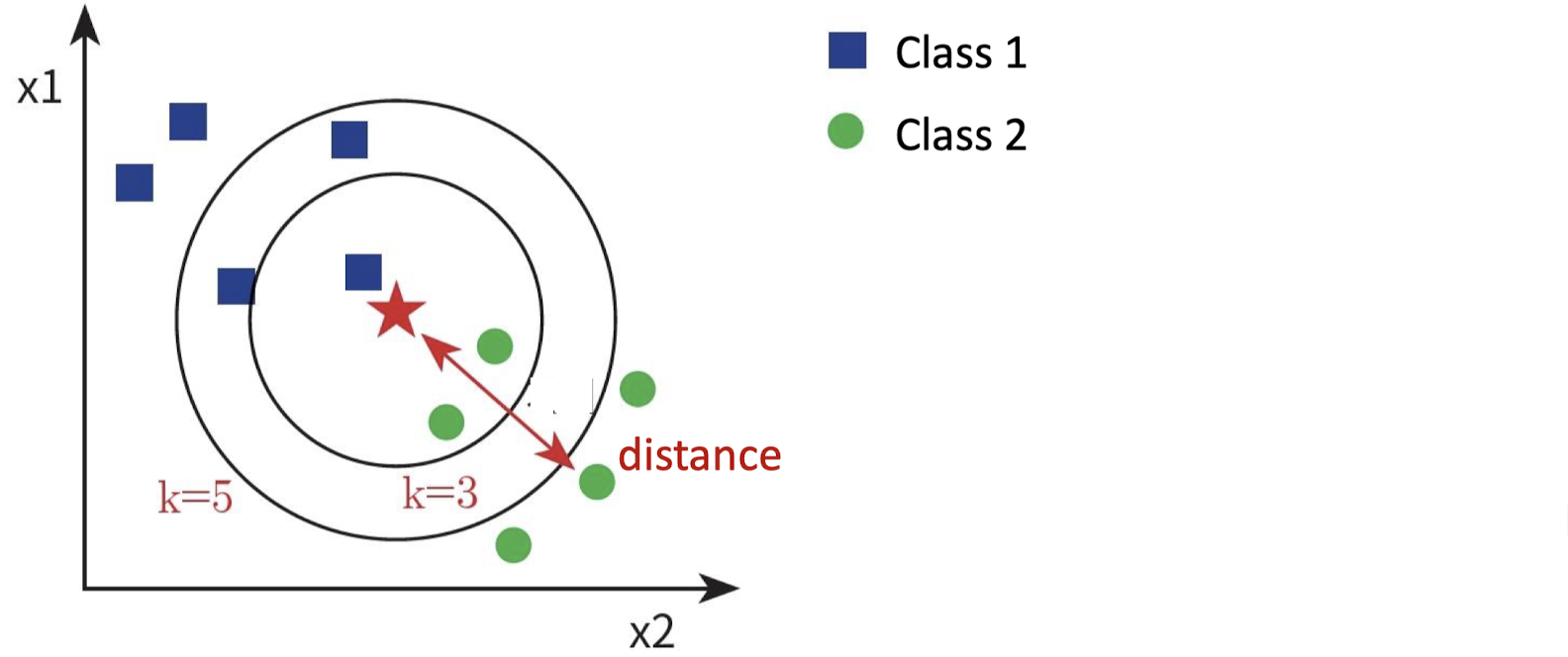
KNN은 Traditional Classification Method 중 하나이다. KNN은 K-Nearest Neighbor의 약자로, 새로운 데이터가 들어왔을 때 말 그대로 K개의 이웃한 점들을 기준으로 다수결 투표를 해서 Class를 결정하는 방법이다.위의 예시에서 k가 3일 때는 class2, k가 5일 때는 class1이 선택된다. 이때 K는 Hyper Parameter로, 우리가 직접 튜닝해야 되는 파라미터이다. 동점 방지를 위해 K는 주로 홀수를 택하여 사용한다.

KNN을 수행하는 절차는 위의 그림과 같다. 이때, 거리를 계산하는 방식에는 여러가지가 있는데, 아래 표를 참고하자.

위의 표에는 대표적인 Distance Metric(거리 측정법)들이 소개되어 있다. Manhattan Distance는 L1, Euclidean Distance는 L2라고도 부른다.

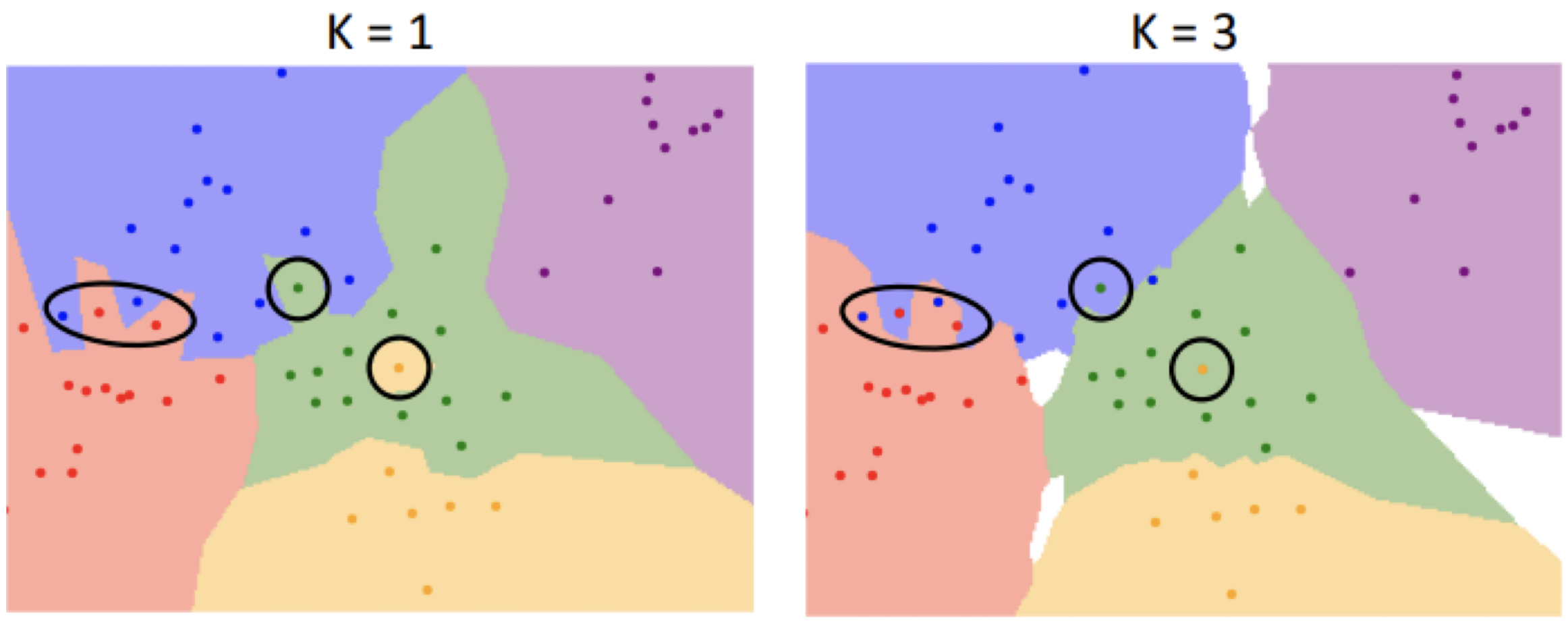
위의 그림을 보면서 KNN의 특징을 정리해보자.

K값에 따라 Boundary가 다르게 결정된다. 즉, 같은 데이터라도 다른 Class로 분류될 수 있다.
투표 결과 동점이 발생하는 경우, 분류가 불가능하기 때문에 사각지대가 생긴다.
평균에서 멀리 떨어진 Outlier들에 의해 Noise가 발생하기도 한다. (동그라미 친 점들)

Hyper Parameter

Hyper Parameter란, 학습 결과로는 알 수 없고, 인간이 직접 튜닝해야 되는 파라미터를 말한다. KNN에서는 K값이나 Distance Metric 등이 Hyper Parameter라고 할 수 있다. 그렇다면 Hyper Parameter를 설정하는 방법에 대해 알아보자.

먼저, 전체 데이터셋을 대상으로 학습하여 Hyper Parameter를 결정하면 새로운 데이터가 들어왔을 때 어떻게 동작할지 예측할 수 없다. 따라서, 전체 데이터셋을 Train Dataset, Validation Dataset, Test Dataset으로 나누고, Validation Dataset을 통해 Hyper Parameter를 결정하고, Test Dataset으로 성능을 검증하는 것이 더 나은 방법이다. 하지만, 학습 데이터가 매우 적은 경우에는 이렇게 하면 각 데이터셋의 다양성이 줄어들기 때문에 신뢰도가 낮아지는 문제가 발생할 수도 있다.

신뢰도가 낮아지는 문제를 해결하기 위해 고안된 방법이 (K-fold) Cross-Validation이다. Cross-Validation에서는 데이터셋을 여러 개의 fold로 나누고, 각각의 fold를 Validation Dataset으로 사용한 뒤 평균을 낸다. 이러한 Cross-Validation를 통해 Hyper Parameter를 튜닝할 수 있다. 하지만 Cross-Validation은 딥러닝에서 그렇게 많이 사용되고 있지는 않다고 한다.