머신러닝에서 자주 사용되는 Gaussian Mixture Model(GMM)을 알아보겠습니다. GMM은 머신러닝에서 Unsupervised Learning(클러스터링)에 많이 활용이 됩니다. 하지만 다른 K-means와 같은 클러스터링 알고리즘과는 다르게 통계적인 용어나 수식 때문에 한 번에 이해하기가 어렵습니다. 이 포스팅에서는 수식 없이 기초적인 통계 수준에서 Gaussian Mixture Model을 이해할 수 있게 글을 써보려고 합니다.

우선 GMM을 알기 위해서는 Mixture Model을 알아야합니다. Mixture Model 전체 분포에서 하위 분포가 존재한다고 보는 모델입니다. 즉, 데이터가 모수를 갖는 여러개의 분포로부터 생성되었다고 가정하는 모델입니다. 책에서는 보통 이를 두고, "Unsupervised Learning의 모수적 접근법"이라고 합니다.

이 중에서 가장 많이 사용되는 가우시안 믹스쳐 모델(GMM)은 데이터가 K개의 정규분포로부터 생성되었다고 보는 모델입니다.

샘플 데이터 생성

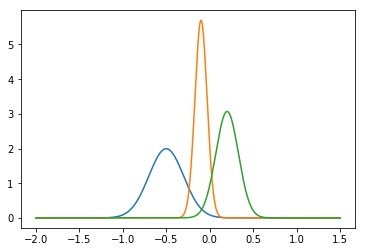
예를 들어, A, B, C라는 세 종류의 정규분포의 PDF(probability density function)를 상상해봅시다. GMM은 데이터가 이 3가지 정규분포중 하나로부터 생성되었으며, 또 그 안에서 random하게 정규분포 형태를 갖고 생성되었다고 보는 모델입니다.

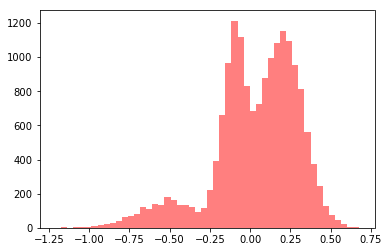
세 종류의 데이터를 모두 합치면 위와 같은 모양이 됩니다. 여러분들은 이 데이터를 보고 "아 왠지 데이터가 3개의 정규분포로부터 생성되었을 것 같아." 라고 생각하고, GMM을 적용시키면 되는 것입니다.

모수 추정

GMM에서의 모수는 두 가지 종류가 있습니다. 첫 번째는 3가지 정규분포 중 확률적으로 어디에서 속해있는가를 나타내는 Weight 값이고, 두 번째, 각각의 정규분포의 모수(평균, 분산)입니다. 첫 번째 종류의 모수를 잠재변수 라고 부르며, 잠재변수가 포함된 모델은 Mixture Model에서의 모수 추정은 MLE(maximum likelihood estimation)으로 구할 수 없기 때문에 EM(Expectation Maximazation)이라고 부르는 알고리즘을 통해 iterative하게 구하게 됩니다. (왜냐하면 잠재변수가 포함되었기 때문에 likelihood function을 미분할 수가 없기 때문입니다. - 이 부분은 EM 알고리즘을 공부하시면 됩니다.) GMM에 대한 이해가 우선이므로, 이 포스트에서는 EM 알고리즘을 통해 Mixture Model의 모수를 추정하는 방법은 다루지 않겠습니다.

sklearn.mixture.GaussianMixture¶

class sklearn.mixture.GaussianMixture(n_components=1, *, covariance_type='full', tol=0.001, reg_covar=1e-06, max_iter=100, n_init=1, init_params='kmeans', weights_init=None, means_init=None, precisions_init=None, random_state=None, warm_start=False, verbose=0, verbose_interval=10)[source]

from sklearn.datasets import load_iris

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

iris = load_iris()
feature_names = ['sepal_length','sepal_width','patal_length','petal_width']

iris_df = pd.DataFrame(iris.data,columns=feature_names)
iris_df['target'] = iris.target

from sklearn.mixture import GaussianMixture

gmm = GaussianMixture(n_components=3,random_state=0)
gmm.fit(iris.data)
gmm_cluster_labels = gmm.predict(iris.data)

iris_df['gmm_cluster'] = gmm_cluster_labels

iris_result = pd.crosstab(iris_df['target'],iris_df['gmm_cluster'])
print(iris_result)

gmm_cluster   0   1   2
target                 
0            50   0   0
1             0   5  45
2             0  50   0

# 클러스터 결과를 시각화

def visualize_cluster_plot(clusterobj,dataframe,label_name,iscenter=True):
    if iscenter :
        centers = clusterobj.cluster_centers_
        
    unique_labels = np.unique(dataframe[label_name].values)
    markers = ['o','s','^','x','*']
    iscenter =False
    
    for label in unique_labels:
        label_cluster = dataframe[dataframe[label_name]==label]
        if label == -1:
            cluster_lagend = 'Noise'
            isNoise=True
        else :
            cluster_lagend = 'Cluster'+str(label)

        # 군집별로 다른 마커로 산점도 적용
        plt.scatter(x=label_cluster['ftr1'],y=label_cluster['ftr2'],marker=markers[label],label=cluster_lagend)

        # 군집별 중심 표현
        if iscenter:
            center_x_y = centers[label]
            plt.scatter(x=center_x_y[0],y=center_x_y[1],s=200,color='gray',alpha=0.9,marker=markers[label])
            plt.scatter(x=center_x_y[0],y=center_x_y[1],s=70,color='gray',edgecolors='k',marker='$%d$' % label)
    
    plt.show()

from sklearn.datasets import make_blobs

x ,y = make_blobs(n_features=2,n_samples=300,centers=3,cluster_std=0.5,random_state=0)

transformation = [[0.6083,-0.63366],[-0.4088,0.8525]]
x_aniso = np.dot(x,transformation)

cluster_df = pd.DataFrame(x_aniso,columns=['ftr1','ftr2'])
cluster_df['target'] = y

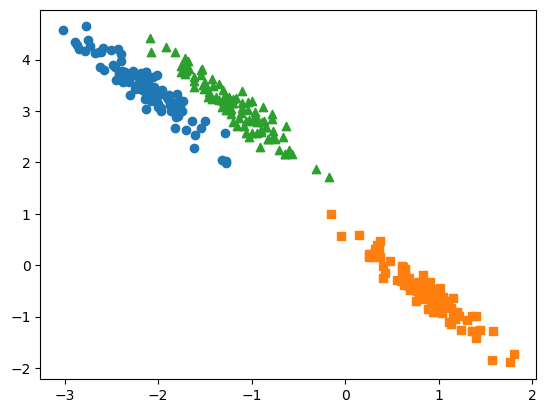
visualize_cluster_plot(None,cluster_df,'target',iscenter=False)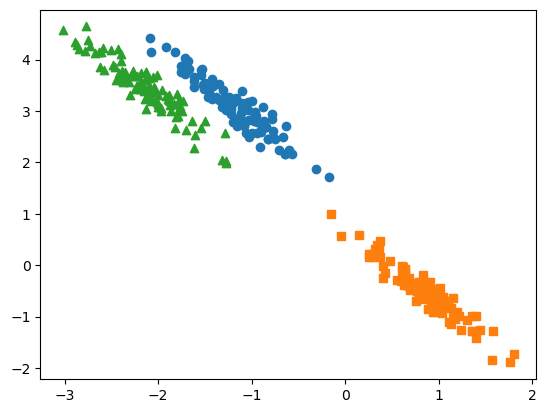

gmm = GaussianMixture(n_components=3,random_state=0)
gmm_label = gmm.fit(x_aniso).predict(x_aniso)
cluster_df['gmm_label'] =gmm_label
visualize_cluster_plot(gmm,cluster_df,'gmm_label',iscenter=False)