다중회귀

다중회귀

• 다중의 독립변수가 있는 회귀 분석
• 여러 개의 독립 변수가 복합적으로 종속 변수에 영향을 미치는 경우 다중 회귀 모형으로 데이터를 표현 할 수 있다.
• 다중 회귀에서 최적 모델을 결정하기 위해 다양한 방법으로 변수를 선택
• 모델이 복잡해지면 과대적합이 발생할 가능성이 있어 이를 방지하고자 다양한 규제를 적용해 모델의 가중치를 제한

from sklearn.datasets import load_diabetes
import pandas as pd
import numpy as np
## 당뇨 데이터를 로드
diabetes = load_diabetes()
x = pd.DataFrame(diabetes.data, columns=diabetes.feature_names)
y = diabetes.target

릿지

• 최소제곱 적합식의 수축 패널티라 불리는 항에 L2 패널티를 추가한 것

from sklearn.linear_model import Ridge

alpha = np.logspace(-3, 1, 5)

data=[]
for i, a in enumerate(alpha):
    ## 정규화의 강도를 지정
    ridge=Ridge(alpha=a)
    ridge.fit(x, y)
    data.append(pd.Series(np.hstack([ridge.coef_])))

df_ridge=pd.DataFrame(data, index=alpha)
df_ridge.columns=x.columns
df_ridge

import matplotlib.pyplot as plt


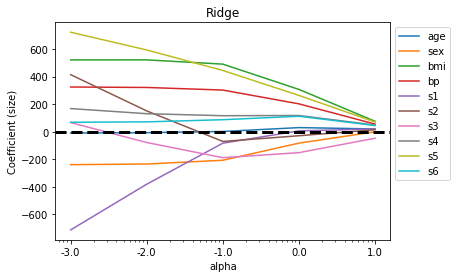
## 알파 값이 증가하면서 회귀계수의 값이 0으로 수렴하는지 시각화를 이용하여 확인
plt.semilogx(df_ridge)
plt.xticks(alpha, labels=np.log10(alpha))
plt.legend(labels=df_ridge.columns, bbox_to_anchor=(1, 1))
plt.title('Ridge')
plt.xlabel('alpha')
plt.ylabel('Coefficient (size)')
plt.axhline(y=0, linestyle='--', color='black', linewidth=3)

from sklearn.linear_model import LinearRegression

## MSE를 사용한 회귀 모델과 비교
## 알파값이 0과 가까운 경우 MSE와 비슷한 사이즈 
## 알파값이 증가하면서 회귀계수가 0에 가까워지는것을 확인

lr=LinearRegression()
lr.fit(x,y)

plt.axhline(y=0, linestyle='--', color='black', linewidth=2)
plt.plot(df_ridge.loc[0.001], '^-', label='Ridge alpa = 0.001')
plt.plot(df_ridge.loc[0.010], 's', label='Ridge alpa = 0.010')
plt.plot(df_ridge.loc[0.100], 'v', label='Ridge alpa = 0.100')
plt.plot(df_ridge.loc[1.000], '*', label='Ridge alpa = 1.000')
plt.plot(df_ridge.loc[10.000], 'o-', label='Ridge alpa = 10.000')

plt.plot(lr.coef_,label='LinearRegression')
plt.xlabel('Feature Names')
plt.ylabel('Coefficient (size)')
plt.legend(bbox_to_anchor=(1,1))

라쏘

• 최소 제곱 적합식의 수축 패널티라 불리는 항에 L1 패널티를 추가한 것
• 릿지 회귀가 변수의 크기가 매우 큰 데이터인 경우 결과를 해석하는데 어려움이 발생하는데 이러한 문제점을 해결하기 위한 방법

from sklearn.linear_model import Lasso

alpha=np.logspace(-3, 1, 5)

data=[]
for i, a in enumerate(alpha):
    lasso=Lasso(alpha=a)
    lasso.fit(x, y)
    data.append(pd.Series(np.hstack([lasso.coef_])))

df_lasso = pd.DataFrame(data, index=alpha)
df_lasso.columns=x.columns
df_lasso

## 알파값이 증가하면서 회귀계수가 0에 도달
## 규제가 강한 라쏘 회귀에서는 bmi과 s5변수만 포함하는 모델이 관찰
## log알파 가 -1에 가까운 경우 bmi s5 bp s3 sex s1 변수가 포함되는 모델이 생성

plt.semilogx(df_lasso)
plt.xticks(alpha, labels=np.log10(alpha))
plt.legend(labels=df_lasso.columns, bbox_to_anchor=(1, 1))
plt.title('Lasso')
plt.xlabel('alpha')
plt.ylabel('Coefficient (size)')
plt.axhline(y=0, linestyle='--', color='black', linewidth=3)

## MSE를 사용한 회귀 모델과 비교
## 알파가 0과 가까운 경우 MSE와 비슷하게 출력
## 알파가 증가하면서 회귀 계수는 0

plt.axhline(y=0, linestyle='--', color='black', linewidth=2)
plt.plot(df_lasso.loc[0.001], '^', label='Lasso alpa = 0.001')
plt.plot(df_lasso.loc[0.010], 's', label='Lasso alpa = 0.010')
plt.plot(df_lasso.loc[0.100], 'v', label='Lasso alpa = 0.100')
plt.plot(df_lasso.loc[1.000], '*', label='Lasso alpa = 1.000')
plt.plot(df_lasso.loc[10.000], 'o-', label='Lasso alpa = 10.000')
plt.plot(lr.coef_,label='LinearRegression')
plt.xlabel('Feature Names')
plt.ylabel('Coefficient (size)')
plt.legend(bbox_to_anchor=(1,1))

엘라스틱넷

• 릿지회귀와 라쏘 회귀를 절충한 알고리즘
• 수축 패널티는 릿지와 회귀의 규제항을 단순히 더한 것, 혼합비율 r을 사용해 조절
• r = 0 이면 릿지회귀, r=1이면 라쏘 회귀

from sklearn.linear_model import ElasticNet

alpha = np.logspace(-3, 1, 5)

data=[]
for i, a in enumerate(alpha):
    ela=ElasticNet(alpha=a, l1_ratio=0.5)
    ela.fit(x, y)
    data.append(pd.Series(np.hstack([ela.coef_])))

df_ela=pd.DataFrame(data, index=alpha)
df_ela.columns=x.columns
df_ela

plt.semilogx(df_ela)
plt.xticks(alpha, labels=np.log10(alpha))
plt.legend(labels=df_ela.columns, bbox_to_anchor=(1, 1))
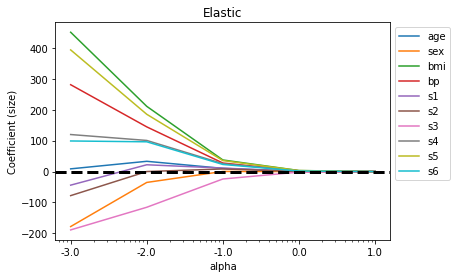
plt.title('Elastic')
plt.xlabel('alpha')
plt.ylabel('Coefficient (size)')
plt.axhline(y=0, linestyle='--', color='black', linewidth=3)

plt.axhline(y=0, linestyle='--', color='black', linewidth=2)
plt.plot(df_ela.loc[0.001], '^-', label='Elastic alpa = 0.001')
plt.plot(df_ela.loc[0.010], 's', label='Elastic alpa = 0.010')
plt.plot(df_ela.loc[0.100], 'v', label='Elastic alpa = 0.100')
plt.plot(df_ela.loc[1.000], '*', label='Elastic alpa = 1.000')
plt.plot(df_ela.loc[10.000], 'o-', label='Elastic alpa = 10.000')
plt.plot(lr.coef_,label='LinearRegression')
plt.xlabel('Feature Names')
plt.ylabel('Coefficient (size)')
plt.legend(bbox_to_anchor=(1,1))