Non-Context-Free Languages

Non-Context-Free Languages

• Regular Language를 공부할 때, Regular Language에 속하지 않는 Language도 공부하였다.
• 이와 비슷하게, Context-Free Language를 공부했으면, Context-Free Language에 속하지 않는 Language도 알아야 한다.
• Regular language의 pummping lemma와 비슷하게, Context-Free Language에는 Pumping length가 있다.
• Pumping Length는 특별한 값으로, context-free language가 "pumped"되기 위한 최소한의 길이이다.
• string은 다섯 부분으로 나뉘며, 두번째 부분과 네번째 부분은

Pumping Lemma for context-free language

만약 $A$가 context-free language라면,$p$ (the pumping length)가 있다. 이 $p$는 만약 임의의 s가 A안에 포함되고, p보다 길이가 길면, s는 다섯 부분인 $s = uvxyz$로 나누어질 수 있다.

임의의 $s = uvxyz$는 다음과 같은 조건을 모두 만족한다.
1. 모든 $i ≥ 0$에 대해서, $s' = uv^ixy^iz ∈ A$
2. $|vy| > 0$
3. $|vxy| ≤ p$

• $v$와 $y$ 모두 $ε$일 순 없다.
• $v,x,y$의 길이를 더하면 아무리 길어져도 $p$보다 길어질 수 없다.

Proof Idea

• $A$는 CFL이며 이를 생성하는 CFG $G$가 있다.
• $A$안에 속하는 임의의 string $s$가 pumped된다는 것을 증명한다.
• $s$가 $A$에 속하는 아주 긴 string이라고 가정하자.
• $s$ 가 $A$에 속하므로, $G$를 derivable하며 그러므로 parse tree를 가진다.
• $s$의 parse tree는 굉장히 높은데, $s$가 길기 때문이다.
  • 이 말은, parset tree는 long path를 가진다.
  • long path는 시작 상태를 root로 가지며, 단 하나의 terminal symbol을 leaf에서 가진다.
• 이 long path에서 어떠한 variable symbol R은 비둘기 집 원리에 따라서 반복되어야 한다.
  

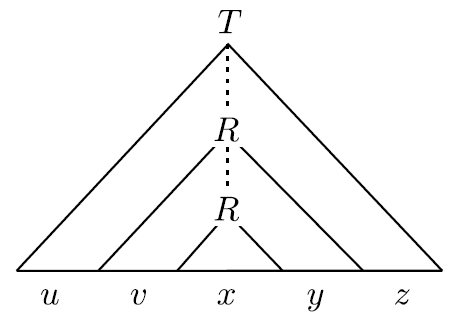
• $s$를 나누어보자
  • variable symbol R은 반복이 무조건 나온다.
  • R이 만드는 string을 x라고 부른다.
  • R이 첫번째 나올 때부터 두번째 나올 때까지 앞부분을 $v$, 뒷부분을 $y$라고 하자.
  • R이 나오기 전에 앞부분을 $u$, 뒷부분을 $z$라고 하자.
• $s'$d은 R을 여러번 반복한다는 의미이다. 다시말해 $v -> v^i$, $y -> y^i$이다.
  

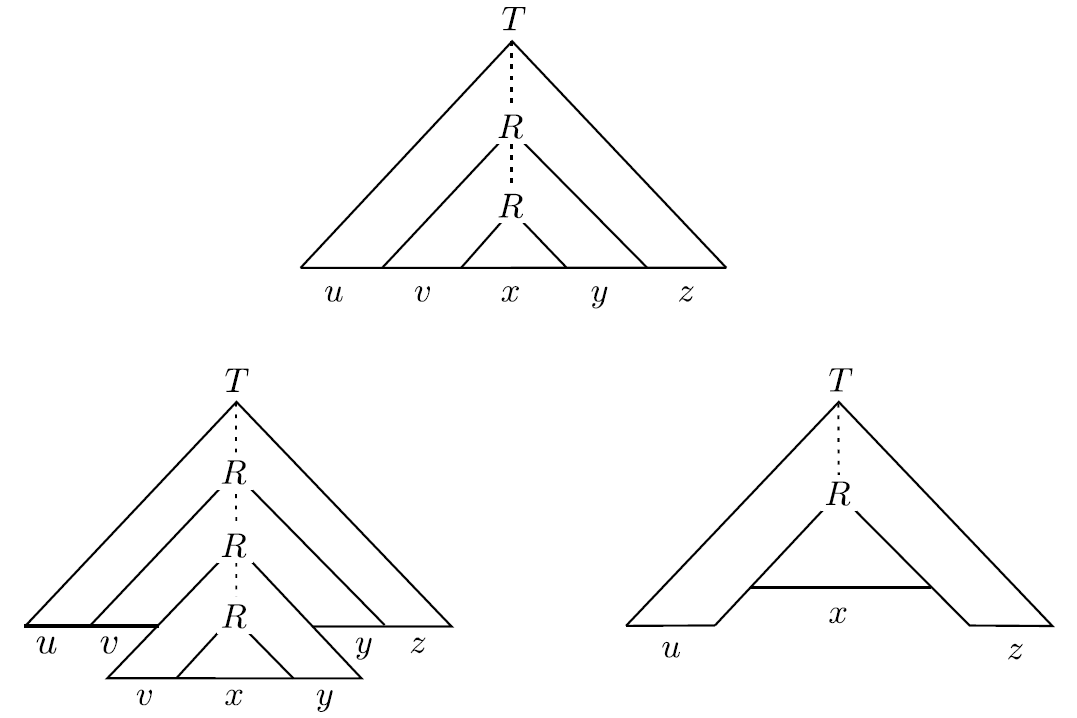
Proof

• CFG $G$는 CFL $A$로부터 나왔다
• $b$는 $G$의 규칙 중 오른쪽에 있는 symbol의 개수 중 최대값이다.
  • $S → 0S1$
  • $S → \#$
    이 두가지 경우에 대해서 $b=3$이다.
• 하나의 노드는 자식을 $b$개 이상 가질 수 없다는 의미이다.
• 다시 말해, 모든 노드는 최대 $b$개의 자식을 가지므로, $h$의 과정을 거친 leaf에는 $b^h$개의 symbol이 생긴다는 의미이다.
• 그러므로 parse tree의 최대 높이가 $h$면, string의 길이는 최대 $b^h$이다.
• 이를 응용하면, 만약 만들어진 string의 길이가 $b^h+1$이면, parse tree는 $h+1$보다 높아야 한다.
• |V|는 $G$의 변수의 개수라고 해보자
• 우리는 $p$를 $b^{|V|+1}$로 정의할 수 있다.
• 이제 s가 A안에 속하고, 길이가 $p$보다 길거나 같으면, parse tree는 $|V|+1$보다 높아야 한다. $b^{|V|+1} > b^{|V|}+1$

• $s$로 인해 만들어지는 parse tree중 하나를 $τ$라 하자.
• $s$가 여러개의 parse tree를 가질 때, $τ$는 node의 개수가 가장 작은 parse tree이다.
• $τ$의 높이는 $|V|+1$보다 높아야 한다.
• 여기서 도출되는 건, $τ$의 길이가 $|V|+1$보다 높으므로 root에서 leaf까지 가는 path는 길이가 적어도 $|V|+1$이다.
• 이 path는 적어도 $|V|+2$개의 노드를 가지고 있다. terminal은 하나이고, 나머지는 variable이다.
• 그러므로 path안에 variable은 $|V|+1$개가 있다.
• 증명하기 전, $R$을 선택할 때 path의 아래서부터 반복되는 $R$을 선택한다.

• upper $R$은 $vxy$를 만든다.
• lower $R$은 $x$를 만든다.
• $i > 1$일 때, lower $R$을 upper $R$로 만든다.
• $i = 0$일 때, upper $R$을 lower $R$로 만든다.

• Condition 2 : $v$와 $y$중 하나는 $ε$이 아니다.
  • 만약 위가 성립한다고 가정하자.
  • $τ$는 $v=ε$ 이고 $y=ε$이다.
  • $s' = uv^0xy^0z$을 만들어보자.
  • 이 때, $s' = s$이다.
  • $τ'$는 $s'$의 node의 개수가 가장 작은 parse tree라고 정의하자. $τ'$는 $τ$보다 노드 개수가 적다.
  • 그러나 $s' = s$이므로 $τ'$는 $s$를 만들 수 있다.
  • 이 말은 $τ$가 $s$의 node개수가 가장 작은 parse tree가 아니라는 의미이다.
  • 그러므로 $τ$의 정의에 대한 모순이 일어난다.
• Condition 3 : $vxy$는 $p$보다 길이가 길 수 없다.
  • upper $R = vxy$가 존재한다.
  • $|V|+1$의 길이인 맨 아래에서부터 path를 따라서 올라갈 때 반복이 나오지 않고 최대한 올라갈 수 있는 높이는 $|V|+1$이다.
  • 높이가 $|V|+1$일 때, symbol의 최대 개수는 $b^{|V|+1} = p$이다.
  • 그러므로 $|vxy| ≤ p$이다.

Example

• $B = \{a^nb^nc^n | n ≥ 0\}$
• 다음에 대해서 context free가 아니라는 것을 증명하자.
• 이를 위해 $B$가 Context-Free라고 가정하자.
• $B$는 pumping lemma를 만족해야한다.
• $p$는 pumping length이다.
• string $s = a^pb^pc^p$를 선택한다.
• $s ∈ B$이며, $|s| ≤ p$임이 명백하다.
• $s = uvxyz$로 나누었을 때 아래 조건을 모두 만족해야 한다.

임의의 $s = uvxyz$는 다음과 같은 조건을 모두 만족한다.
1. 모든 $i ≥ 0$에 대해서, $s' = uv^ixy^iz ∈ A$
2. $|vy| > 0$
3. $|vxy| ≤ p$

• 첫번째로, Condition 2에 의해 $v$와 $y$중 하나는 $ε$이 아니다.
• 다음으로 우리는 2가지 상황을 고려할 수 있다.

1. $v$와 $y$는 하나의 symbol만 가지고 있다. 다시 말해 $a,b,c$중 오직 하나만 가져야 한다.
   • $s' = uv^2xy^2z$를 가정해보자.
   • $uv^2xy^2z$는 $a,b,c$의 개수가 모두 같을 수 없다.
   • 만약 $v$가 $a$만 가지면, $y$는 $a$만 가지거나 $b$만 가지거나 $c$만 가진다.
   • 그러므로 $a,b,c$중 최대 두개는 늘어나고 하나는 그대로이다.
   • 만약 $v$가 $b$만 가지면, $y$는 $b$만 가지거나 $c$만 가진다.
   • 그러므로 $b,c$는 가지는 범위에 따라서 늘어나고 $a$는 그대로이다.
   • 만약 $v$가 $c$만 가지면, $y$는 $c$만 가진다..
   • 그러므로 $c$는 늘어나고 $a,b$는 그대로이다.
   • 그러므로 개수는 모두 같을 수 없다.
2. $v$와 $y$는 두개 이상의 symbol을 가지고 있다. 다시 말해 $a,b,c$가 바뀌는 경계선을 가지고 있다.
   • $s' = uv^2xy^2z$를 가정해 보자.
   • $v$와 $y$는 두개 이상의 symbol을 가지고 있으므로 패턴에 어긋나게 된다.

• $C = \{a^ib^jc^k | 0 ≤ i ≤ j ≤ k\}$
• 다음에 대해서 context free가 아니라는 것을 증명하자.
• 이를 위해 $C$가 Context-Free라고 가정하자.
• $C$는 pumping lemma를 만족해야한다.
• $p$는 pumping length이다.
• string $s = a^pb^pc^p$를 선택한다.
• $s ∈ C$이며, $|s| ≤ p$임이 명백하다.
• $s = uvxyz$로 나누었을 때 아래 조건을 모두 만족해야 한다.

임의의 $s = uvxyz$는 다음과 같은 조건을 모두 만족한다.
1. 모든 $i ≥ 0$에 대해서, $s' = uv^ixy^iz ∈ A$
2. $|vy| > 0$
3. $|vxy| ≤ p$

1. $v$와 $y$는 하나의 symbol만 가지고 있다. $v$,$y$는 $a,b,c$ 3개의 symbol중 하나에는 없다.
   1.a $a$쪽에 없는 경우이다. $uv^0xy^0z = uxz$는 $a$의 개수가 동일하지만 $b$나 $c$는 $a$보다 개수가 작아지므로 조건을 만족하지 못한다.
   1.b $b$쪽에 없는 경우이다. 이러면 $a$나 $c$는 무조건 나와야 한다. 왜냐하면 $|v|$와 $|y|$는 0보다 크기 때문이다.

   • $a$가 나오면 $uv^2xy^2z = uxz$을 사용한다. 이는 $a$의 개수가 $b$보다 커지므로 조건을 만족하지 못한다.
   • $c$가 나오면 $uv^0xy^0z = uxz$을 사용한다. 이는 $c$의 개수가 $b$보다 작아지므로 조건을 만족하지 못한다.

   1.c $c$쪽에 없는 경우이다. $uv^2xy^2z$는 $c$의 개수가 동일하지만 $a$나 $b$는 $c$보다 개수가 커지므로 조건을 만족하지 못한다.

2. $v$와 $y$는 두개 이상의 symbol을 가지고 있다. 다시 말해 $a,b,c$가 바뀌는 경계선을 가지고 있다.

   • $s' = uv^2xy^2z$를 가정해 보자.
   • $v$와 $y$는 두개 이상의 symbol을 가지고 있으므로 패턴에 어긋나게 된다.

• $D = \{ ww | w ∈ \{0,1\}^* \}$
• 다음에 대해서 context free가 아니라는 것을 증명하자.
• 이를 위해 $D$가 Context-Free라고 가정하자.
• $D$는 pumping lemma를 만족해야한다.
• $p$는 pumping length이다.
• $s$를 찾는 과정은 굉장히 오래 걸릴 것이다. 어떻게 보면 안된다고 생각할 수도 있다.
• 만약 string $s = 0^p10^p1$를 선택했다고 본다.(이 경우는 통과하지 못함)
• $s ∈ D$이며, $|s| ≤ p$임이 명백하다.
  
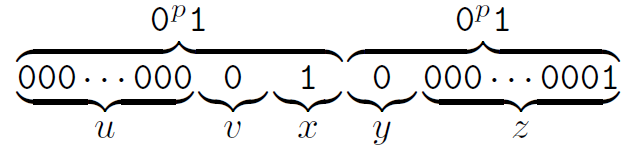
• $uv^0xy^0z = uxz$는 $0^{p-1}10^{p-1}1$이 된다. 이것은 조건에 만족한다.
• $uv^ixy^iz$는 $0^{p+i-1}10^{p+i-1}1$이 된다. 이것은 조건에 만족한다.
• 그러므로 잘못 뽑은 string $s = 0^p10^p1$는 귀류법을 증명하지 못ㅎ나다.

• string $s = 0^p1^p0^p1^p$를 선택한다.
• $s ∈ D$이며, $|s| ≤ p$임이 명백하다.
• $s = uvxyz$이고 $|vxy|≤ p$다.
• 이 경우 3가지 과정을 통해 증명할 수 있다.

1. $vxy$는 $s$의 가운데를 포함해야 한다.
   • 만약 $s$ 절반의 앞에 있다고 해보자.
   • $uv^2xy^2z$는 $s$ 절반의 앞에 숫자들이 추가된다는 의미이다.
   • 이 경우 $uv^2xy^2z$의 가운데는 앞으로 옮겨간다.
   • 그러나 이 경우 가운데가 1의 영역을 침범하므로 $w$가 앞은 0으로 시작하고 뒤는 1로 시작하게 된다.
   • $s$ 절반의 뒤에 있는 경우도 비슷하다.
   • 그러므로 $vxy$는 $s$의 가운데를 포함해야 한다.
2. $vxy$는 $s$의 가운데를 포함해야 한다.
   • 이 경우 $uv^0xy^0z = uxz$는 $0^p1^i0^j1^p$가 된다.
   • $i≠p$이거나 $j≠p$이다.
   • 그러므로 같은 $w$가 나올 수 없다.