The Church-Turing Thesis

Turing Machines

• 우리는 지금까지 여러가지 모델들을 봐왔다.
• Finite Automata는 작은 개수의 메모리에 대해서 좋은 모델이다.
• Pushdown Automata는 stack방식에 적절한 무한한 메모리에 대해서 표현할 수 있는 좋은 모델이다.
• 그런데도 불구하고 풀 수 없는 문제들은 존재한다.
• 지금부터 소개하는 모델은 이런 문제들을 풀기 위해 만든 모델이며, 현대 컴퓨터의 기반이다.

• Alun Turing은 Turing Machine이라는 아주 강력한(powerful) 모델을 생각해냈다.
• Finite automation과 비슷하지만, 메모리의 수가 무한하며 메모리에 제약이 없다.
• 이러한 특성 때문에 현대 컴퓨터의 기반이 되었다.
• 튜링 머신은 현대 컴퓨터가 할 수 있는 모든 것을 할 수 있다.
• 그러나 알아둬야 하는 건, 튜링 머신 조차도 풀 수 없는 문제들이 존재한다.
• 이것은 사실, 튜링 머신의 한계가 아닌 Computation의 한계이다. 다시 말해 컴퓨터의 한계를 넘어서는 일이다.

What is Turing Machine?

• Turing machine model은 무한한 tape과 무한한 memory를 가진다.
• Tape은 읽거나 쓸 수 있고 tape 위를 돌아다닐 수 있다. 이는 head를 통해 이뤄진다.
• 맨 처음에 tape이 만들어질 때, tape은 모든 곳에 blank를 가지고 있다.
  
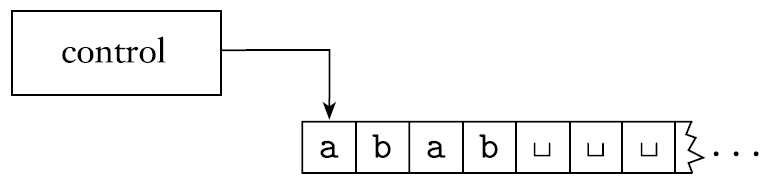
• 만약 Turing machine이 정보를 저장하고 싶으면, tape에 write하면 된다.
• 만약 Turing machine이 저장된 정보를 읽고 싶으면, tape에 written된 것을 head를 움직여서 읽으면 된다.
• Turing machine은 output을 만들 때 까지 computation을 계속한다.
  • 여기서 output은 accept와 reject이다.
  • accept하고 싶으면 accept state에 들어가면 된다.
  • reject하고 싶으면 Finite automata와는 다르게 reject state에 들어가야 한다.
• Turing Machine은 head를 통해서 자신이 어디를 보고 있는지를 조정할 수 있다. 이러한 특성 때문에 head가 옮겨졌을 때 더 진행할건지 그만둘건지를 알 수 없다. 그렇기 때문에 reject state가 필요하다.
• accepting state에 들어가지 않거나 rejecting state에 들어가지 않으면, 평생 원하는 대로 할 것이다. 다시 말해 halting하지 않는다.
• 위의 말을 정리하여 finite automata와 turing machine의 차이점을 정리하자.

1. Turing machine은 write와 read가 가능하다.
2. Read-write하는 head는 왼쪽이나 오른쪽으로 이동 가능하다.
3. Tape는 무한하다.
4. 들어오는 즉시 accept하거나 reject하는 특별한 state가 존재한다.

Introduce Turing Machines

• $B = \{ w\#w | w ∈ \{0, 1\}^* \}$
• $B$라는 language를 test하는 Turing machine $M_1$이 있다.
• 우리의 목표는 들어오는 input이 $B$에 적합한지를 파악해야 한다.
• 가장 먼저 떠올릴 수 있는 방법은 지그재그로 보는 것이다.
  • $011\#001$이라는 input이 있다고 하자.
  • 맨 앞의 symbol을 본다.
    • 만약 $0,1$이면 기억하고 $0,1$을 $X$로 바꾼다.
    • 만약 $\#$면 accept state로 간다.
    • 만약 $X$면 $0,1,\#$이 나올 때 까지 뒤에 것을 보는 걸 반복한다.
  • $\#$뒤에 있는 symbol을 본다.
    • 기억한 $0,1$과 같으면 $0,1$을 $X$로 바꾼다.
    • 기억한 $0,1$과 다르면 바로 reject state로 간다.
• 다음은 $M_1$이 011000#011000에 대해서 test하는 것을 그림으로 나타낸 것이다.
  
• Turing machine의 핵심은 transition function이다. 왜냐하면 작동하는 방식 모든 것을 담고 있기 때문이다.
• Turing machine의 transition function $δ$은 $Q × Γ → Q × Γ× \{L, R\}$로 나타낼 수 있다.
• 이 말은 다음과 같다.
  • 지금 상태와 input을 받는다.
  • 다음 상태와 바껴야 할 input, head의 이동 위치 Left or Right를 말해준다.
  • 이는 Turing machine은 read만 하는 것이 아닌 write가 가능하기 때문이다.
• 내가 $q$상태에 있을 때 tape head는 $a$를 가리키고 있으면, $a$를 $b$로 바꾼 뒤 상태 $r$로 간다. 이후 tape의 head는 L or R한다.
• $δ(q, a) = (r, b, L)$

Formal Definition of Turing machine

튜링 머신은 7-tuple $(Q, Σ, Γ, δ, q_0, q_{accept}, q_{reject})$이며, $Q, Σ, Γ$은 유한한 집합이다.
1. $Q$는 상태들의 집합
2. $Σ$는 blank를 나타내는 blakc symbol $⊔$을 제외한 input alphabet
3. $Γ$는 tape alphabet이며, $⊔ ∈ Γ$이고 $Σ ⊆ Γ$이다.
4. $δ : Q × Γ → Q × Γ× \{L, R\}$는 transition function
5. $q_0 ∈ Q$는 start state
6. $q_{accept} ∈ Q$는 accept state
7. $q_{reject} ∈ Q$는 reject state이며, $q_{reject} ≠ q_{accept}$

• $M = (Q, Σ, Γ, δ, q_0, q_{accept}, q_{reject})$은 다음을 따른다.
• input $w = w_1w_2 . . . w_n ∈ Σ^∗$에 대해서 tape의 맨 왼쪽부터 n번째까지 쓰며, 나머지는 blank이다.
• head는 tape의 맨 왼쪽에서 시작한다.
• 첫번재 blank가 나오면 그 전까지가 input이라고 할 수 있다. 왜냐하면 $Σ$에는 blank $⊔$가 없기 때문이다.
• 만약 내 head가 맨 왼쪽에 있는데 transition function이 왼쪽으로 가라 했으면 맨 왼쪽에 가만히 있는다.
• $q_{accept}$ 또는 $q_{reject}$에 들어오지 않는 이상 computation은 계속된다.
• 위에 둘 다 들어오지 않으면, Machine은 영원히 computation한다. 다시 말해 forever한다.
  • 이러한 이유 때문에 TD(Turing Decidable)와 TR(Turing Recognizable)로 나뉜다.

Configuration

• Turing machine이 게산할 때, 현재 state를 바꾸고, 현재 tape content를 바꾸며, 현재 head location을 바꾼다.
• 이 3개의 요소들의 특정한 조합을 configuration이라고 부른다.
  • 현재 상태
  • 현재 tape 전체의 content
  • 현재 head의 위치
• configuration은 다음과 같이 정의할 수 있다.
  • 상태 $q$
  • string $u$와 $v$ / $u,v ∈ Γ$
  • configuraton은 $uqv$
  • 이 말은 현재 상태는 $q$이고, 현재 tape의 content는 $uv$라고 할 수 있으며, head의 위치는 $v$의 맨 처음에 있다고 할 수 있다.
• $1011q_701111$를 보자.
  • tape는 $101101111$다.
  • 현재 상태는 $q_7$이다.
  • head는 두번째 나오는 0에 위치해있다.
    
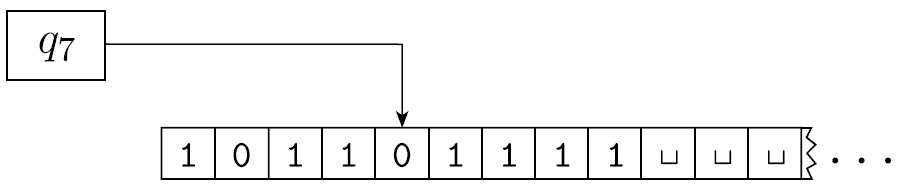
• Configuration $C_1$이 $C_2$를 yield한다는 것은 $C_1$에서 $C_2$로 간다는 의미이다.
• 다음을 생각해보자.
  • $a,b,c ∈ Γ$
  • $u, v∈Γ^∗$
  • $q_i$와$q_j$
  • $C_1 = uaq_ibv$ / $C_2 = uq_jacv$
  • $δ(q_i, b) = (q_j , c, L)$
  • 이것은 Turing Machine이 왼쪽으로 움직인, 다시 말해 leftward한 것이다.
• rightward한 것의 예시는 $δ(q_i, b) = (q_j , c, R)$라고 할 수 있다.
• head가 맨 왼쪽에 있을 때
  • head가 input의 맨 왼쪽에 있을 때 leftrward하게 되면, $q_ibv$가 $q_jcv$를 yield한다.
  • head가 input의 맨 왼쪽에 있을 때 rightward하게 되면, $q_ibv$가 $cq_jv$를 yield한다.
• head가 input의 맨 오른쪽에 있을 때
  • head가 input의 맨 오른쪽에 있을 때는 $uaq_i$는 $uaq_i⊔$와 같은 의미이다.
  • 그러므로 일반적인 상황과 동일하다고 할 수 있다.
• Start configuration은 $q_0w$이며, 시작 상태 $q_0$에서 시작하여 head가 맨 왼쪽에 있는 모습을 의미한다.
• Accepting configuration일 때, configuration의 상태는 $q_{accept}$이다.
• Rejecting configuration일 때, configuration의 상태는 $q_{reject}$이다.
• Accepting configuration과 Rejecting configuration을 합쳐서 Halting configuration이라고 부른다.
• $q_{accept}$와 $q_{reject}$가 추가됨에 따라, transition function을 고칠 필요가 있다.
• $δ : Q' × Γ → Q × Γ× {L, R}$이며, where $Q'$는 $Q$에서 $q_{accept}$와 $q_{reject}$를 뺀 것이다.

Turing Machine $M$은 일련의 configuration $C_1, C_2,...,C_k$에 대해서 input $w$를 다음과 같은 조건하에 accept한다.
1. $C_1$은 input w에 대한 turing machine M의 start configuration이다.
2. 각각의 $C_i$은 $C_{i+1}$을 yield한다.
3. $C_k$는 accepting configuration이다.

• Turing Machine $M$이 recognize하는 모든 language를 $L(M)$으로 표기한다.

Turing-recognizable

어떤 Turing machine이 language를 recognize한다면 그 language를 Turing-recognizable이라고 부른다.

• Turing machine은 지금까지와 달리, 3가지의 가능성이 존재한다.
• 바로 accept, reject, looping이다.
• 어떤 Turing machine은 $q_{reject}$에 들어와서 rejecting하거나, 아니면 looping한다.
• 그러나 looping하는건지, rejecting하는 건지를 파악하는 건 어렵다.
  • 긴 시간을 가지면 해결된다! 라고 말해도 얼마나 긴 시간?인지 알 수 없다.
• 이러한 이유 때문에, 우리는 영원히 loop하지 않는 turing machine을 보길 원한다. 다시 말해, Turing machine이 모든 input에 대해서 halt하는 turing machine을 원한다.
• 이러한 machine들을 decider라고 부른다. 왜냐하면 accept거나 reject이기 때문이다.
• Decider가 recognize하는 language들을 decide라고 부른다.

어떤 Turing machine이 특정한 language를 decides하면, 그 language를 Turing-decidable 또는 decidable이라고 한다.

Example 1

• $M_1 = (Q, Σ, Γ, δ, q_1, q_{accept}, q_{reject})$는 language $B = \{w\#w | w ∈ {0, 1}^∗\}$를 deciding 하는 Turing machine이다. 다시말해 decider다.
• $Q =\{q_1, . . . , q_8, q_{accept}, q_{reject}\}$
• $Σ = {0, 1, \#}$이고 $Γ = {0, 1, \#, X, ⊔}$이다.
  
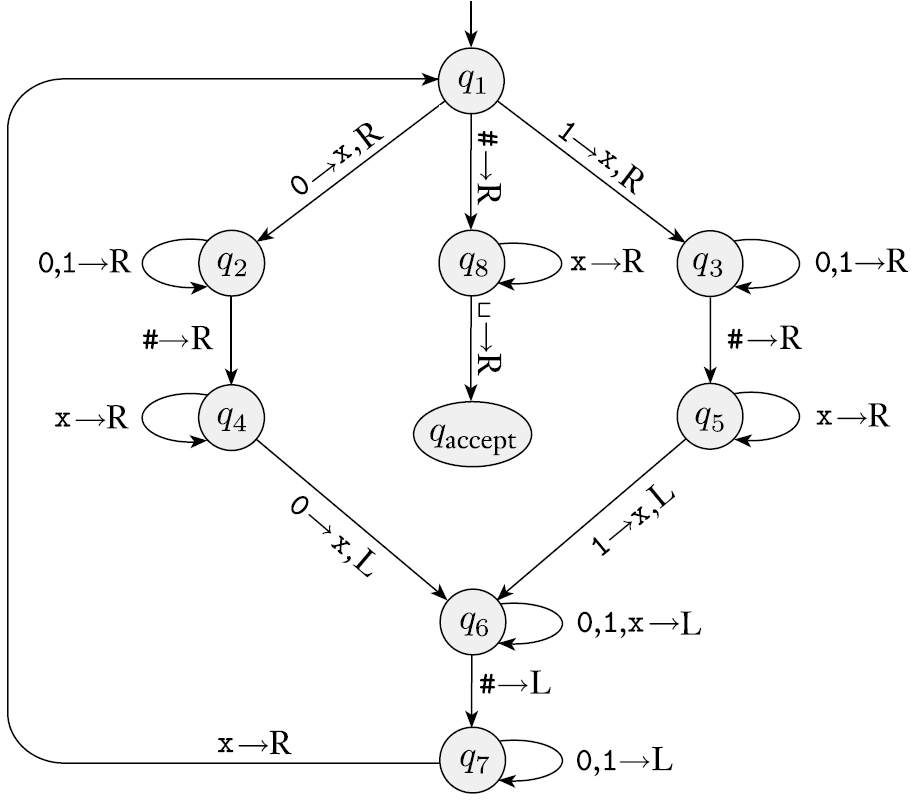
• $q_1$은 symbol들에 대해서 판단을 해주는 state이다. 0,1을 만나면 $X$로 바꾸고 오른쪽으로 이동한다. $\#$을 만나면 오른쪽으로 이동한다.
• $q_2, q_3, q_4, q_5$는 $q_1$에서 만난 symbol을 다시 만날 때 까지 오른쪽으로 가는 state다.
• 만약 $q_4, q_5$에서 $q_1$에서 고친 symbol을 만나면 $q_6$로 이동한다.
• $q_6, q_7$은 처리를 완료하여 다시 $q_1$으로 돌아가기 위한 state다. $\#$이 나온 후 왼쪽에 존재하는 $X$가 나올 때 까지 왼쪽으로 이동한다. $X$가 나오면 다시 오른쪽으로 이동한다.
• 여기서 $q_1$에 대한 추가 설명을 하자. $q_1$에서 $\#$가 나오려면 이전에 아무것도 없거나 $X$여야만 나올 수 있다.
• $\#$앞과 뒤가 똑같은지, 다시말해 0,1 symbol이 모두 없어져 $\#, X, ⊔$만 남았는지를 파악하기 위해 $q_1$과 $q_8$이 사용된다. 조건을 만족하면 $q_{accept}$로 간다.
• 원래라면 reject state와 reject state로 가는 transition이 있어야 한다. 간략화를 위해 생략한다.

Example 2

• Turing Machine ${M_2}$가 decide하는 language는 다음과 같다.
• $A=\{0^{2^n}|n ≥ 0\}$
• 0의 개수가 $2^n$개 나온다.
• 기본 전략은 다음과 같다.
  • 0이 1개 있으면 accept한다.
  • 0이 1개 이상 있으면 2로 나눈다.
    • 나누었을 때 0이 짝수개거나 0이 1개 있으면 accept한다.
    • 나누었을 때 0이 1개가 아닌 홀수개면 reject한다.
  • 위 Case가 아니면 반복한다.
    
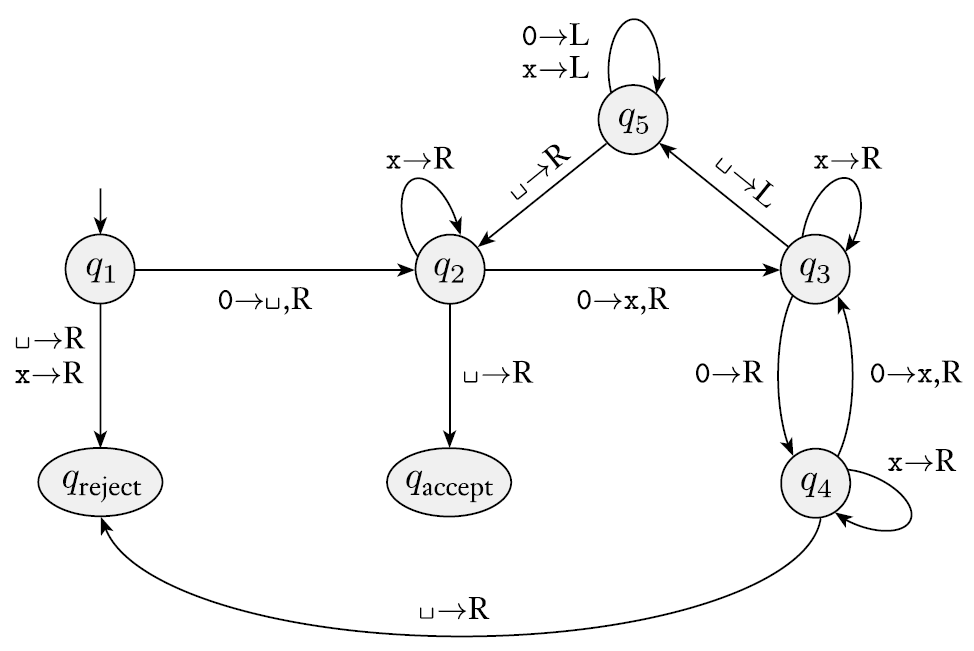
• $q_1$은 0이 0개 있는 상태다.
• $q_2$는 0이 1개 있는 상태다.
• $q_3, q_4$은 각각 0의 개수가 짝수인지 홀수인지 판별해준다.
• $q_5$는 0의 개수가 짝수인 경우를 받아서 header를 맨 앞(맨 앞은 $⊔$로 변해 있음)으로 보내주고, 상태는 $q_2$으로 보내준다.

Example 3

• $M_3 = (Q, Σ, Γ, δ, q_1, q_{accept}, q_{reject})$는 C를 decide한다.
• $C = \{a^ib^jc^k|i * j = k 이고 i,j,k ≥ 1\}$
• 이 예제를 통해 Turing Machine이 곱하기가 가능하다는 것을 보여준다.
• M_3는 다음과 같이 동작해야 한다.

1. 들어오는 input은 $a^+b^+c^+$처럼 생겨야 한다. 만약 이렇지 않으면 reject한다.
2. 확인했으면 다시 처음으로 (left-hand end) 돌아간다.
3. $a$가 나오면 지우고 $b$가 나올 때 까지 오른쪽으로 간다. $b$가 나오면 $c$와 대응되도록 하나씩 지운다. 만약 $c$가 다 지워졌는데 $b$가 남았으면 reject한다.
   4.지우는 과정이 끝나면 지운 $b$를 다시 복원한다. 만약 $a$가 있으면 3번으로 돌아간다. 만약 $a$가 없으면 $c$가 하나도 없는지 확인한다. 있으면 reject하며 없으면 accept한다.

• 첫번째 조건에 대해서 $M_3$는 Finite automaton처럼 작동할 수 있다.
• 두번째 조건은 쉬워 보인다. 하지만 left-hand end를 어떻게 판별할 건지를 정해야 한다.
  • right-hand end를 판별하는 건 쉬운데, $⊔$가 나오면 오른쪽 끝이기 때문이다.
  • 그러나 left-hand end를 판별하는 건 right-hand end만큼 쉽진 않다.
  • 그렇기 때문에 맨 처음 시작할 때 있는 symbol을 $⊔$로 바꿔줌으로 left-hand end를 판별할 수 있다.
• 이제 세번째 조건과 네번째 조건에 대해서 turing machine을 완성하면 된다.

Example 4

• $M_4$는 "element distinctness problem" 을 해결하는 Turing Machine이다. 이는 모든 원소가 전부 다른지를 판별한다.
• $M_4$는 $\{0,1\}$로 구성되어 있는 string들이 $\#$로 나누어져 있는데, 이들이 모두 다른지를 확인한다.
• $E = \{ \# x_1 \# x_2 \# ... \# x_l | x_i ∈ \{0, 1\}^∗, i ≠j -> x_i ≠ x_j\}$
• $M_4$는 현재 위치를 확인하기 위해서 mark를 가진다.
  • mark는 $\overset●\#$로 표시한다.
• $M_4$가 동작하는 방식은 다음과 같다.

1. 맨 왼쪽을 $\overset●\#$로 바꾼다.
   • 만약 맨 왼쪽이 $⊔$면 accept한다.
   • 만약 맨 왼쪽이 $\#$면, 다음 단계로 간다.
   • 위 둘이 아니라면 reject한다.
2. 다음 $\#$을 찾을 때 까지 오른쪽으로 이동한다.
   • 만약 $\#$이 안나오고 $⊔$가 나오면, $x_1$만 존재하므로, accept한다.
   • 만약 나오면 $\overset●\#$로 바꾼다.
3. 왔다갔다하면서 $\overset●\#$의 옆에 있는 string을 비교한다.
   • 두 string이 같으면 reject한다.
   • 두 string이 같지 않으면 다음 단계로 간다.
4. $\overset●\#$중 오른쪽에 있는 것을 $\#$로 복원시키고 다음 $\#$을 찾을 때 까지 오른쪽으로 이동시킨다.
   • 만약 $⊔$가 나올 때 까지 $\#$가 없으면, 다음을 따른다.
     • 처음 $\overset●\#$(오른쪽)가 나오면 $\#$로 복원시킨다.
     • 두번째 $\overset●\#$(왼쪽)가 나오면 $\#$로 복원시키고 다음 $\#$을 찾을 때 까지 오른쪽으로 이동한다.
     • $\#$가 있으면 $\overset●\#$로 바꾸고 다음 단계로 간다.
     • $\#$가 없으면, accept한다.
5. 3으로 간다.