Variants of Turing Machine
- Turing machine을 활용하면, tape을 여러개 가지며 nondeterminism한 Turing machine을 만들 수 있다.
- 우리가 지금까지 배운 DTM(Deterministic Turing Machine)과는 사뭇 달라보이는 NTM(Non-Deterministic Turing Machine)을 배우게 될 것이다.
- 여기서 중요한 건, 이라는 것이다. 다시 말해 둘의 파워는 같다.
Stay Turing Machine
- 우리의 정의에서 head는 왼쪽이나 오른쪽으로 움직인다.
- 이 Turing Machine은 head를 움직이지 않을 수 있다.
- 이 Turing Machine은 일반 Turing Machine이 할 수 있는 것보다 더 많은 일을 할 수 있을까? 정답은 아니다.
- 멈춰있는 상태를 무조건 움직여야 하는 상태로 바꿀 수 있다. 왜냐하면 한 쪽으로 움직인 후 아무것도 하지 않고 다시 돌아오면 되기 때문이다.
- 이는 두개의 Turing Machine의 동일성을 나타낸다. 다시 말해 한 TM이 다른 TM이 하는 일을 따라할 수 있으면 두개는 같다고 할 수 있다.
Multitape Turing Machine
- Multitape Turing Machine은 여러개의 tape이 존재하는 Turing Machine이다.
- 모든 tape는 각각의 head가 있으며, 모두 read나 write가 가능하다.
- input은 맨 처음 tape에 들어가며, 나머지 tape는 blank로 차있다.
- 이 Turing Machine은 일반 Turing Machine이 할 수 있는 것보다 더 많은 일을 할 수 있을까? 정답은 아니다.
Equivalent of Turing Machines
- MTM은 tape를 여러개 가진다. 각각의 tape는 reading, writing, moving이 가능하며 동시에 이루어진다.
- MTM의 transition function은 로 정의할 수 있다. 여기서 는 tape의 개수다.
- 현재 상태에서, 다음 상태로 간다.
- 각각의 tape는 head에 있는 symbol을 규칙에 따라 바꾼다.
- 각각의 tape는 규칙에 따라 움직인다.
모든 Multitape Turing Machine은 동일한 동작을 하는 Single-Tape Turing Machine이 존재한다.
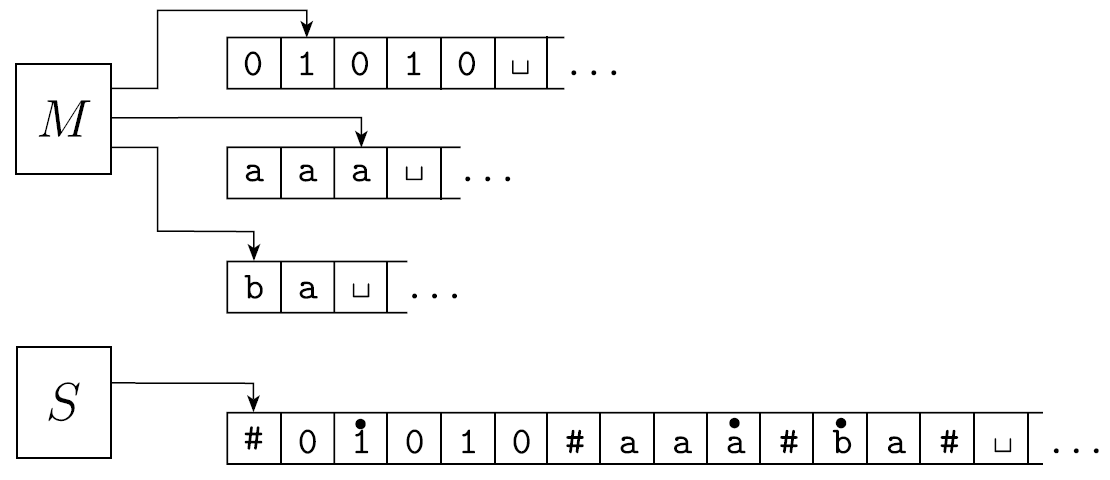
- 어떤 MTM 을 똑같은 TM 로 바꿔보자.
- 은 개의 tape를 가지고 있다. 그러므로 는 하나의 tape에 개의 tape 내용들을 모두 적는다.
- 이 때 사실은 MTM의 다른 tape이라고 구분해주는 구분자()를 내용들 사이에 넣어서 구분해준다.
- 구분자를 통해 tape를 구분할 수는 있어졌지만, head가 어디 있는지는 알지 못한다.
- 이를 해결하기 위해 mark()를 사용한다.
- mark를 통해 각각의 tape에 해당되는 head가 어디를 가리키고 있는지를 알게 되었다.
- 이를 virtual head라고 부른다.
- 현재 정보를 다 나타냈지만, 동작을 나타내지는 못했다. 동작은 아래와 같이 표현한다.
- input 에 대해서 MTM 과 동일한 역할을 하는 TM 는 다음 과정을 따른다.
- 위에서 말한 규칙들을 이용해서 k개의 tape을 하나의 tape에 나타낸다.
- 와 같이 표현할 수 있다.
- 의 한번의 움직임을 하기 위해서, 는 첫번째 부터 k+1번째 까지 쭉 진행하며 읽어본다.
- 이를 통해 각각의 virtual head를 알게 된다.
- 이후 다시 첫번째 로 되돌아가면서 head에 있는 symbol을 고친다.
- 이 과정에서 head가 이동을 하므로, virtual head 또한 움직여야 한다.
- virtual head를 옮기는 일은 되돌아가면서 해도 되고, 한번 했다가 다시 진행하면서 찍어도 무방하다.
- 만약 가 어떠한 virtual head를 위에 놓게 되는 경우가 있다. 다시 말해 가 되는 경우가 있다.
- 이 경우는 특정 tape의 head가 를 가리킨다는 뜻이다.
- 그러므로 우리는 를 만들어줘야 한다.
- 를 만들어주기 위해, 뒤로 한칸씩 밀어주고 를 넣어준다.
어떤 language에 대해서 Turing-recognizable이 존재하면, Multitape Turing Machine 또한 존재한다. 역도 동일하다.
Nondeterministic Turing Machines
- Nondeterministic Turing machine은 여러가지 길로 갈 수 있는 Turing machine이다.
- NFA와 비슷하게 여러가지 가능성으로 진행할 수 있으며, 각각의 지점마다 개별적인 계산이 가능하다.
- NTM의 transition function은 로 정의할 수 있다. Power set이라는 뜻이다.
- NTM의 동작 방식을 그리면 Tree처럼 그려진다.
- input이 들어왔을 때, 각각의 branch를 따라서 accept state에 도달하면, NTM은 input을 accept한다.
모든 Nondeterministic Turing Machine은 동일한 동작을 하는 Turing Machine이 존재한다.
- NTM 과 동일한 동작을 하는 TM 가 있다고 하자.
- 증명의 핵심은 가 비결정적인 의 모든 계산을 수행할 수 있어야 한다.
- 가 accept state로 통하는 branch를 발견한다면, 는 accept한다.
- 은 input 에 대해서 tree를 만든다.
- Tree 각각의 branch는 nondeterminism을 나타낸다.
- Tree 각각의 node는 N의 configuration을 나타낸다.
- Tree의 root는 start configuration이다.
- TM 는 accepting configuration을 찾아야 한다.
- 안 좋은 방법 중 하나는 tree에 대해서 DFS를 수행하는 것이다.
- 만약 DFS를 수행하면 가 infinite한 branch에 들어가서 accepting configuration을 놓칠 수 있기 때문이다.
- 그나마 나은 방법 중 하나는 tree에 대해서 BFS를 수행하는 것이다.
- BFS를 수행하는 것은 시간이 오래 걸려도 가 accepting configuration을 만날 때 까지 탐색한다는 게 보장된다.
- BFS의 문제는 상태를 복구하기 위해 과거로 되돌아가는 과정이다.
- TM 는 Tape를 3개 가진다.
- 이는 전의 증명을 통해 MTM이어도 TM이 존재한다는 것을 증명했다.
- Tape 1 : input string이 들어간다. 읽을수만 있으며 쓸 수 없다.
- Tape 2 : input string을 복사한다. 그 뒤 branch에 해당하는 일들을 수행한다. 실질적으로 계산이 수행되는 공간이다.
- Tape 3 : 가 의 길을 따라갈 수 있도록 하는 공간이다.
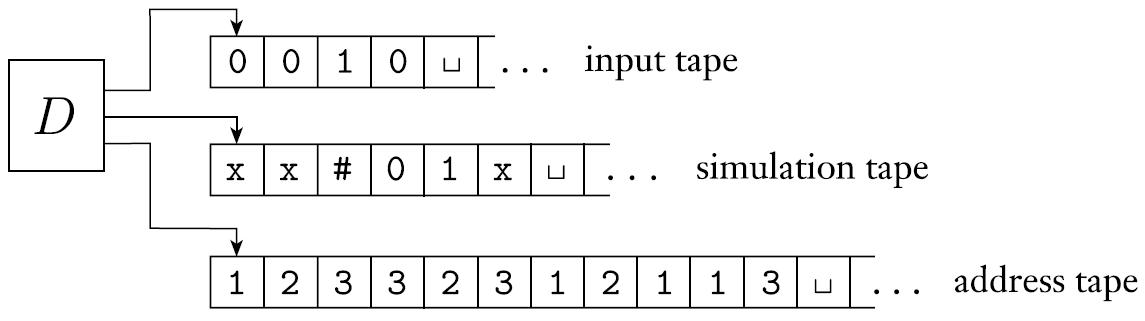
- Tape 3에 나와있는 데이터를 생각해보자.
- 모든 노드는 최대 개의 자식을 가질 수 있다. 는 가능성이 제일 많은 노드의 자식 개수이다.
- 모든 노드는 각각 주소를 가지고 있으며, 로 만든 string이다.
- 을 생각해보자. 먼저 root에서 2번째 자식으로 간다. 그 후 3번째 자식으로 간다. 마지막으로 1번째 자식으로 간다.
- empty string은 root를 나타낸다.
- 어떤 string은 의 동작과 맞지 않을 수 있다. 이런 경우는 생각하지 않는다.
- 우리는 이제 를 정의할 수 있다.
- 맨 처음에는 tape 1은 input 로 차 있으며, tape 2,3는 비어있다.
- tape 1을 tape 2에 복사한다.
- 이 input 에 대해서 수행할 수 있는 비결정적 계산을 tape 2에 수행한다. 자세히 살펴보자.
- 에 대해서 계산을 하기 전에 tape 3를 읽으며 어떻게 계산해야 할 지를 먼저 파악한다.
- tape 3에 따라서 의 tree에서 정의한 자식으로 이동한다.
- accepting configuration을 만나면, input에 대해서 accept한다.
- rejecting configuration을 만나면, 4번 순서로 간다.
- tape 3에 남아있는 symbol이 존재하지 않거나 string에 맞는 자식이 없으면, 4번 순서로 간다.
- tape 3에 있는 string을 다음 string으로 바꾼다.
- 2번 순서로 돌아가서 끝날 때 까지 반복한다.
어떤 language에 대해서 Turing-recognizable이 존재하면, nondeterministic Turing Machine 또한 존재한다. 역도 동일하다.
Enumerators
- 어떤 사람들은 Turing-recognizable language를 recursively enumerable language라고 부른다.
- 이 용어는 Turing machine의 일종인 enumerator에서 나왔다.
A language is Turing-recognizable if and only if some enumerator enumerates
it.
We ski
Equivalence with Other Models
- 우리는 Turing machine의 여러가지 변형을 봤고 power가 동일함을 확인했다.
- 이를 넘어서 Turing machine은 무궁무진한 변형 버전이 있다.
- 어떤 Variant Turing machine은 Turing machine과 같지만, 어떤건 다르다.
- 공유하는 중요한 특징은 다음과 같다.
- unrestricted access to unlimited memory
