The Definition of Algorithm

Definition of Algorithm

• 알고리즘이란 어떤 일을 수행하는 절차나 방법의 집합이다.
• 알고리즘은 procedures나 recipe로 불린다.
• 알고리즘은 수학에서부터 나왔으며, 수학자들이 여러가지 일에 알고리즘을 사용하곤 했다.
• 20세기 이전까지는 알고리즘에 대한 정확한 정의가 이루어지지 않았다.
• 이때까지는 알고리즘이 정확히 무엇을 할 수 있으며, 어떤 과정을 통해 작동하는지에 대한 설명이 부족했다.

Hilbert's Problems

• 1900년대에 David Hilber는 수학 학회에서 23개의 문제를 정의함으로써, 많은 수학자들이 한 세기동안 매달리도록 만들었다.
• 23개의 문제 중 10번째 문제가 바로 알고리즘에 관련된 문제이다,
• polynomial(다항식)은 상수와 변수로 이루어진 하나의 식이다.
• 상수는 정수(integer)로만 이루어져있다.
  • $6 · x · x · x · y · z · z = 6x^3yz^2$에서 상수는 $6$ / 변수는 $x,y,z$
• root(근)는 다항식을 0으로 만드는 변수의 값을 뜻한다.
• 어떤 polynomial은 정수 근(integral root)을 같는 반면, 어떤 polynomial은 그렇지 못하다.
  • 예를 들어보자.
  • $6x^3yz^2 + 3xy^2 − x^3 − 10$라는 다항식이 있다.
  • 알고리즘의 근은 $x = 5, y = 3, z = 0$이다.
  • 그러므로 모든 근이 정수 근을 가지므로
• Hilbert의 10번째 문제는 다항식이 정수 근을 같는지 확인하는 알고리즘을 만들어 내는 것이다.
• 문제에서는 정확히 알고리즘을 만들어내라고 하지 않았지만, 유한한 과정을 통해서 증명하라고 하면서 사실상 알고리즘을 만들어내라고 하였다.
• 중요하게 볼 것은, Hilbert는 다항식이 정수 근을 가지는지 판별하는 알고리즘이 존재한다는 것을 보장하며, 이를 찾아내라고 한 것이다.
• 우리가 현대에 와서 밝혀낸 것은, 이러한 알고리즘은 없다는 것이며, 찾아낼 수 없다는 것이다.
• 다시 말해 algorithmically unsolvable이다.
• 이는 좀 허무한 결말이긴 하지만, 중요하기도 하다.
• 알고리즘이 할 수 없는 일이 있다는 것을 알아내면서, 알고리즘이 무엇을 할 수 있는지에 대한 논의가 시작되었다.

Church-Turing thesis

• 1936년에 Alonzo Church와 Alan Turing은 어떤 기계를 만들려고 했다. Entscheidungsproblem
• Church은 λ-calculus라고 불리는 시스템을 통해서 알고리즘을 정의하려고 하였다.
• Turing은 이를 machine일고 불렀다.
• 이 둘은 같다.
• Church-Turing thesis
• 이는 알고리즘과 Turing machine이 동일함을 알려준다.

Hilbert's Problem in Chuch-Turing thesis

• $D$ = {p | p is a polynomial with an integral root}라는 language가 있다고 하자.
• Hilbert's Problem은 $D$가 decidable하다고 믿었기에, 이 decider를 가져오라고 하였다.
• 하지만 $D$는 Turing-recognizable이기 때문에 decidable하지 않았다.
• 이를 증명하기 전에, 간단한 문제에 대해서 생각해보자.
• $D$를 축소시켜서 변수를 하나만 가지는 $D_1$을 생각해보기로 하였다.
  • $4x^3 − 2x^2 + x − 7$
• $D_1$ = {p | p is a polynomial over x with an integral root}.
• Turing machine TM $M_1$은 $D_1$을 recognize한다. $M_1$은 다음과 같다.
  • p라는 다항식은 변수로 x만 가진다. 이 다항식을 input으로 받는다.
  • 0부터 시작해서 1,-1,2,-2 ... 돌아가며 식이 0이 나오면 accept한다.
  • 이것을 따를 때 p가 integral root를 가지면 accept한다.
  • 이것을 따를 때 p가 integral root를 가지지 않으면, 영원히 작동할 것이다.
• $M_1$을 $D_1$으로 바꾼다.
• $D_1$은 범위가 정해져 있어 그 범위를 넘어가면 integral root를 받지 않게 되므로 reject한다. 이는 수학적으로 정해져있다.
• root는 $±k\frac{c_{max}}{c_1}$에서 나온다.
• Matijasevic’s theorem은 이 범위를 정하는 것이 불가능하다고 말한다.

• 튜링 머신에 대해서 얘기했지만, 지금부터는 알고리즘에 대해서 얘기한다.
• 튜링 머신은 알고리즘에 대한 precise model로 사용할 수 있다.
• 들어가기 전에, 튜링 머신 알고리즘을 어떻게 설명할 것 인지에 대해서 먼저 알아보자.
• formal description은 첫번째 단계이다. Turing machine의 상태, transition function, alphabet등등 formal description으로 나타내며 제일 lowest-level이다.
• implementation description는 두번째 단계이다. 자연어나 언어를 섞어가며 작동하는 방식에 대해서 말한다. 예를 들어 head가 tape을 고치고 왼쪽으로 이동한다 등등... 이 단계에서 state나 transition function은 잘 나타내지 않는다.
• high-level description는 세번째 단계이다. 자연어나 언어를 이용하여 알고리즘이 작동하는 방식에 대해서 설명한다. head나 tape같은 용어를 잘 사용하지 않으며 우리가 사용하는 주변 용어로 알고리즘을 설명한다.
• 이제 튜링 머신을 나타내는 방식을 보자
• Turing machine의 input은 string이다.
• input으로 string을 받지 않고 object를 받아도, string으로 표현할 수 있다.
• String은 polynomials, graphs, grammars, automata, 이것들을 합친 것 모두를 나타낼 수 있다.
• Object $O$를 string으로 나타낸 것을 로 표현한다.
• Object가 여러개여서 $O_1, O_2, ... , O_k$여도 <$O_1, O_2, ... , O_k$>처럼 나타낼 수 있다.
• 알고리즘은 맨 처음에 input에 대해서 설명한다.
• input을 간단하게 $w$로 나타낼 것이다. 여기서 input이 string이 아니었어도 <$A$>같은 encoding 방법을 통해 string으로 바꿀 수 있으며, 바꿀 수 없으면 reject할 것이다.
• $A$는 undirected graphs that are connected에 모든 것의 집합이다.
• 모든 노드가 edge와 node를 통해 다른 노드로 갈 수 있으면 graph는 connected하다.
• $A$ = {⟨$G$⟩ | $G$는 연결된 무방향 그래프이다.}
• TM M은 A를 decide하는 turing machine이다.
• M = “On input ⟨$G$⟩, the encoding of a graph $G$:

1. $G$의 임의의 처음 node에 mark한다.
2. 새로운 노드 하나가 mark될 때 까지 mark한다.
3. 다른 node에 대해서 주변에 mark된 node가 있으면 자신을 mark한다.
4. 모든 노드가 mark되어 있으면 accept하고, 아니면 reject한다.

• 이제 implementation-level로 가자.
• 먼저, 우리는 G를 어떻게 encode할 것인지를 먼저 봐야 한다.
  
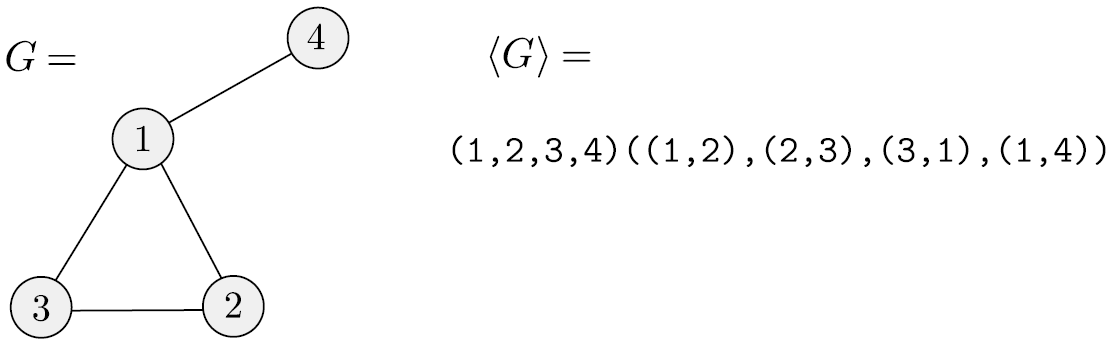
• M이 input G를 받으면, 먼저 graph의 형식을 통과하는지 확인한다.
  • 두개의 list로 나누어져있으며, 처음 list에 들어가는 숫자는 모두 다르고 두번째 list에 들어가는 숫자들의 pair는 정수여야 한다.
• 그 후 여러가지를 확인한다.

1. node는 반복이 없다
2. edge list에 나오는 모든 node는 node list에도 존재해야 한다.

• 이제 알고리즘에 대해서 기술한다.

1. 맨 왼쪽 정수에 dotmark한다
2. dotmark되지 않은 다른 정수에 underlinemark한다.