Decidability

• 이전에 우리는 현대 컴퓨터의 모습인 Turing machine과 이의 variable을 배웠다.
• 또한 Algorithm == Turing machine을 얘기하기도 했다.
• 지금부터 우리는 알고리즘이 풀 수 없는 문제들에 대해서 얘기할 것이다.
• 풀 수 없는 문제들을 배우는 이유는 다음과 같다.
  • 어떤 문제에 대한 정답이 있는지 없는지 알면 못 푸는 문제의 정답을 알려는 쓸데 없는 짓을 하지 않을 수 있다.
  • 문제에 대한 정답이 있다는 것을 알고 깊게 고민할 수 있다.
  • 이에 대한 상상력이 자극되므로 도움을 받을 수 있다.

Decidable Language

• Language는 다시 말해 문제(Problem)이다.
• 우리는 decidable한 langauge를 먼저 살펴본다.
• 예시로, 주어진 regular language에 어떤 string이 들어가는지 확인하는 algorithm 또한 decidable language이다.
• decidable을 살펴보는 것은 undecidable을 이해하는 것에도 도움이 된다.

Computational Problems in finite automata

• 우리는 finite automata의 계산적 문제를 먼저 살펴본다
• 어떠한 string에 대해서 accept시키는 finite automaton이 존재하는지 알아보는 algorithm을 보자.
• DFA에 대한 acceptance problem은 "주어진 string을 accept시키는 특정한 DFA가 language로 표현되는가?"이다.
• DFA와 DFA가 accept하는 string을 모두 가지는 language를 $A_{DFA}$라고 하자.
• $A_{DFA} = \{⟨B, w⟩ |B$는 input string $w$를 accept시키는 DFA$\}$
• $B$가 accept하는 모든 string은 모두 $A_{DFA}$안에 있으며, accept하지 않는 string은 $A_{DFA}$안에 존재하지 않는다.
• 이에 따라 yes / no로 대답할 수 있다.
• $⟨B, w⟩$가 $A_{DFA}$의 member인지 확인하는 것이 Finite automata의 Computational Problem이다.

$A_{DFA}$는 decidable language이다.

• $A_{DFA}$를 따라하는 Tuting Machine $M$을 만든다.
• $M$ = $B$는 DFA이고 $w$는 string이다. 이를 묶은 input $<B,w>$에 대해서

1. $w$를 $B$에 simulate한다.
2. $B$가 accept state에서 끝나면 $A_{DFA}$는 accept이며, 아니면 reject이다.

• 먼저 input $<B,w>$를 정의해야한다.
• DFA $B$와 string $w$를 같이 나타낸다.
• B = (Q, Σ, δ, q0, F)로 표현할 수 있다.
• TM M의 tape에 Q, Σ, δ, q0, F를 순서대로 표기한다.
• 이후에 tape에 input을 표기한다.
• 아니면, M은 reject한다.
• M은 바로 simulation 할 수 있다.
  • B의 start state부분을 읽어서 State에 mark한다.
  • 이후 받은 input의 첫번째를 mark한다.
  • state와 input의 mark 상태를 파악하고 transition function에 다시 mark한다.
  • transition function의 mark상태에 따라 state를 다시 mark한다.
  • 만약 input이 끝났을 때 accept state의 요소 중 하나가 mark되어 있으면 accept하고, 아니면 reject한다.
  • 반복한다.
• 비슷하게 NFA도 증명할 수 있다.
• $A_{NFA} = \{⟨B, w⟩ |B$는 NFA이며 input string $w$를 accept한다.$\}$

$A_{NFA}$는 decidable language이다.

• $A_{NFA}$를 따라하는 Tuting Machine $N$을 만든다.
• $B$는 NFA이고 $w$는 string이다. 이를 묶은 input $<B,w>$에 대해서

1. $B$와 동일한 DFA $C$를 만든다. 다시 말해 $B$를 $C$로 변환한다.
2. 위에서 사용한 TM $M$을 $<C,w>$에 대해서 실행한다.
3. TM $M$이 accept하면 accept이고, 아니면 reject이다.

---

• Finite Automaton이지만, 조금 다른 것을 보자.
• DFA를 하나 주고, DFA가 recognize하는 language가 아무것도 없는지를 알려주는 알고리즘이 있다고 하자.
• $E_{DFA} = \{⟨A⟩ |A$는 DFA이며 $L(A) = ∅$이다.$\}$

$E_{DFA}$는 decidable language이다.

• DFA가 어떤 string을 accept한다는 건 어떤 string이 start state에서 시작해서 accept state에 도달해야 한다는 의미이다.
• 어디까지 도달할 수 있는 지를 reachable하다고 하다.
• $E_{DFA}$를 따라하는 Turing Machine $T$을 만든다.
• $T$ = $A$는 DFA이며 input으로 받는다.

1. $A$의 start state에 Mark한다.
2. 새롭게 mark되는 state가 없을 때까지 반복한다.
3. mark된 state로부터 Transition Function을 통해 갈 수 있는 state는 모두 mark한다.
4. 만약 accept state가 mark되었으면 accept하며, 아니면 reject한다.

---

• 두 DFA가 같은지 판별해주는 알고리즘이 있다고 하자.
• $EQ_{DFA} = \{⟨A,B⟩ |A,B$는 DFA이며 $L(A) = L(B)$이다.$\}$

$EQ_{DFA}$는 decidable language이다.

• $A,B$로부터 새로운 DFA $C$를 도출해낸다.
• L(C)는 L(A) xor L(B)이다.
• Symmetric difference : $L(C) = (L(A) ∩ \overset\_{L(B)}) ∪ ( \overset\_{L(A)} ∩ L(B))$
  
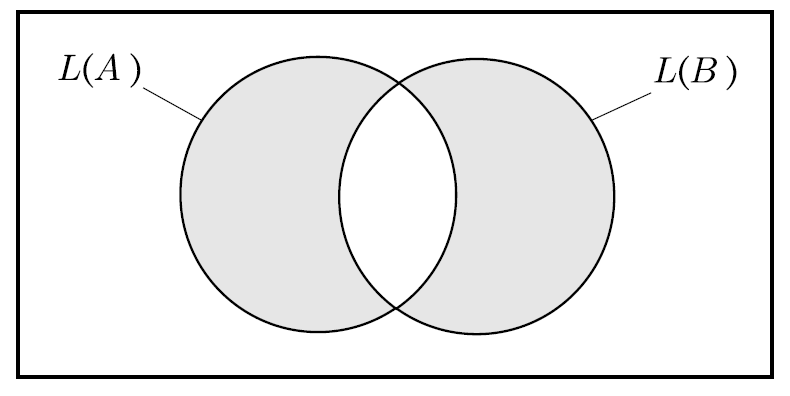
• 만약 $L(C) = ∅$이면 $L(A) = L(B)$이며 역도 같다.
• DFA가 어떤 string을 accept한다는 건 어떤 string이 start state에서 시작해서 accept state에 도달해야 한다는 의미이다.
• 어디까지 도달할 수 있는 지를 reachable하다고 하다.
• $E_{DFA}$를 따라하는 Turing Machine $F$을 만든다.
• $F$ = $⟨A,B⟩$의 $A$,$B$는 DFA이며 input으로 받는다.

1. $A,B$를 이용하여 DFA $C$를 만든다.
2. 위에서 만든 TM $T$를 input $⟨C⟩$에 대해서 수행한다.
3. 만약 T가 acccept하면, F는 accept하며 reject하면 reject한다.

Decidable Problems Context-free Language

• 특정한 CFG가 string $w$를 만들 수 있는지 없는지 판별해주는 알고리즘이 있다고 하자.
• $A_{CFG} = \{⟨G,w⟩ |G$는 CFG이며 string $w$를 accept한다.$\}$

$A_{CFG}$는 decidable language이다.

• string w에 대한 CFG G가 있을 때, G가 w를 만들어내는지 알고 싶다.
• 여기서 생각해 볼 것은 G가 derivation을 통해 나아간다는 점이다.
  • 그렇다면 G가 w를 만들 때 derivation을 따라가다 보면 w에 도달할 것이다.
  • 그러나 여기서 문제가 생긴다. 만약 G가 w를 만들지 못하면 계속 derivation을 따라갈 것이고, 만약 무한한 derivation을 만들 수 있다면 halt하지 못하게 된다.
  • 그렇다면 $A_{CFG}$와 동일한 Turing machine은 recognized할 수 있지만, 이것이 decider는 아니게 된다.
• 이를 해결하는 방법은 G를 Chomsky normal form으로 만드는 것이다.

• Chomsky Normal Form은 다음과 같은 조건을 만족하는 grammer다.
  A → BC
  A → a
• terminal a와 A, B, C은 variable이며, B와 C는 start variable이 아니다.
• S → ε, S가 start variable일때만 ε로 바꿀 수 있다.

• Chomsky normal form은 w의 길이가 n일때, derivation은 최대 2n-1개가 존재할 수 있다.

• 그러므로 Chomsky normal form을 사용하면 2n-1개까지 보게 되므로 무한히 계산하지 않게 된다.

• $A_{CFG}$를 따라하는 Turing Machine $S$을 만든다.

• $S$ = $⟨G,w⟩$의 $G$는 CFG이며 $w$는 string이다. 이들의 묶음을 input으로 받는다.

1. $G$를 동일한 grammer를 가진 Chomsky normal form으로 바꾼다.
2. $n$의 길이를 가지는 string $w$에 대해서, derication은 $2n-1$개가 존재한다. 예외적으로 $n=0$이면 1 step을 거친다.
3. 만약 $w$를 만드는 어떠한 derivation이 존재하면 accept하며, 아니면 reject한다.

---

• 여기서 확장시켜보자.

모든 context-free language는 decidable하다.

• 어떤 CFL $A$가 있다.
• 우리는 $A$가 decidable하다는 것을 증명해야한다.
• 하나의 안 좋은 아이디어는 A를 recognize하는 PDA를 바로 TM으로 변환하는 것이다.
  • 어렵지 않아 보이는데, 왜냐면 PDA는 stack이므로 가리키는 head가 맨 위에 있기 때문에, TM도 위를 가리키게 하면 구현될 것 같이 보인다.
  • 또한, PDA는 nondeterministic이지만, TM또한 nondeterministic이므로 쉬워 보인다.
  • 한마디로 TM의 Power가 더 크기 때문에 쉬워보인다.
• 왜 이게 안 좋은 아이디어냐면, PDA의 어떤 갈래(branch)에서는 영원히 계산할지도 모른다는 것이다.
  • 예를 들어 다음을 보자.
  • $ε, ε→A$
  • $ε, A→ε$
  • 두 상태를 번갈아서 가면, PDA는 A를 push하고, 다시 A를 pop하고, 다시 A를 push하고... 영원히 같은 작업을 반복하게 된다.
• 이렇게 되면 TM이 decidable하지 않게 되며, 이것은 PDA가 가리키는 context-free language가 decidable하지 않다는 의미이다.
• 그래서 우리가 전에 만든 $S$를 이용해야 한다.

1. 위에서 만든 $S$에 $⟨G,w⟩$를 넣는다.
2. $S$가 accept하면, $M_G$는 accept한다. $S$가 reject하면, $M_G$는 reject한다.

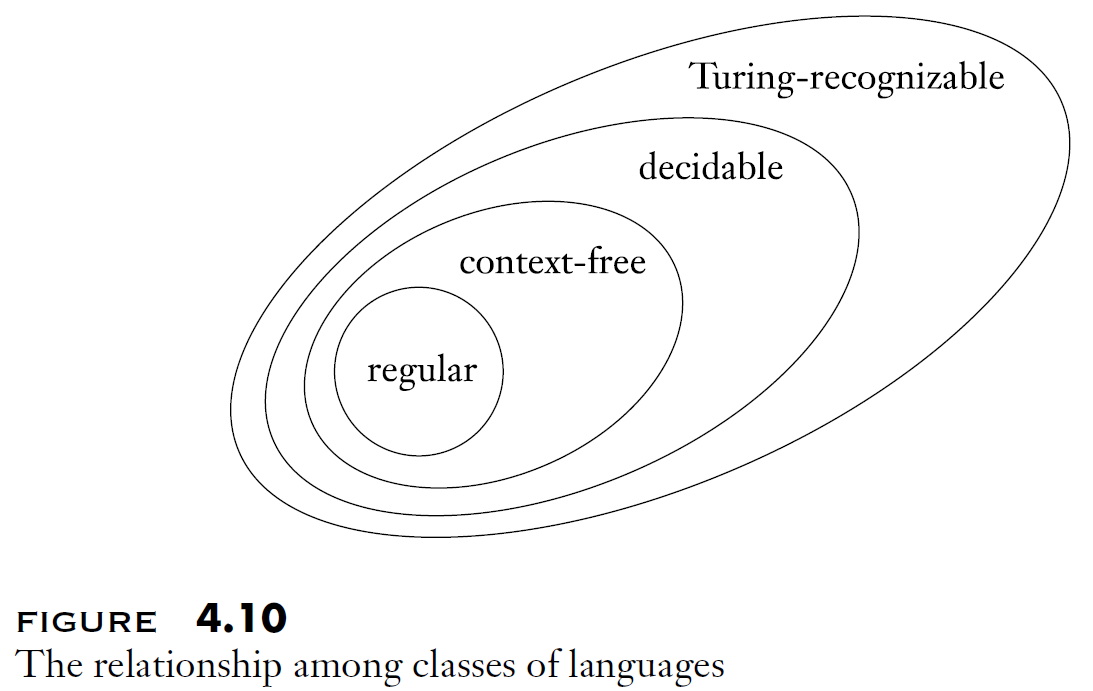
이를 통해 각각의 language들간의 관계를 정리할 수 있다.