C++ 우선순위 큐

200원짜리개발자·2023년 6월 15일

C++자료구조

C++

목록 보기

12/39

강의 보고 공부한 것을 정리하는 목적으로 작성된 글이므로 틀린 점이 있을 수 있음에 양해 부탁드립니다. (피드백 환영입니다)

우선순위 큐는 언제 사용할까?
우선순위 큐는 가장 좋은 케이스 하나를 추출할 때 유용하게 사용된다.

예시

만약 Vector가 있고 안에 데이터 10개 중에서 가장 큰 숫자를 찾기 위해서는 어떠한 방법이 좋을까?

정렬을 하여 가장 큰 값을 가져오거나 하나하나 스캔을 하여서 가장 큰 수를 찾는 방법이 있을 것이다.
만약 정렬을 하여 구한다면 제일 빠른 정렬이 시간복잡도가 O(NlogN)이다.
만약 하나하나 스캔을 한다면 시간복잡도는 O(N)일 것이다.

일단 최소 O(N)이라는 것을 알 수 있다.

하지만 여기서 우선순위 큐라는 것을 배운다면
이것들 보다 더 효율적이게 구할 수 있다.

일단 사용은

#include <queue>

priority_queue<int> pq;

이런식으로 할 수 있지만 어떤식으로 돌아가는지가 더 중요할 것이다.

힙 트리(feat.이진 트리)

일단 우선순위 큐에 핵심인 힙 트리를 알아야 한다.
힙 트리는 완전 이진 트리 중 한 가지기에 이진 트리의 개념도 알아야 한다.

이진 트리

이진 트리는 각 노드가 최대 두 개의 자식 노드를 가지는 트리이다.

이진 검색 트리의 특징으로는

왼쪽을 타고 가면 현재 값보다 작다.
오른쪽을 타고 가면 현재 값보다 크다.
이런식으로 규칙을 정해주면 검색을 하는데 굉장히 편해진다.

하지만 데이터가 추가 하다가

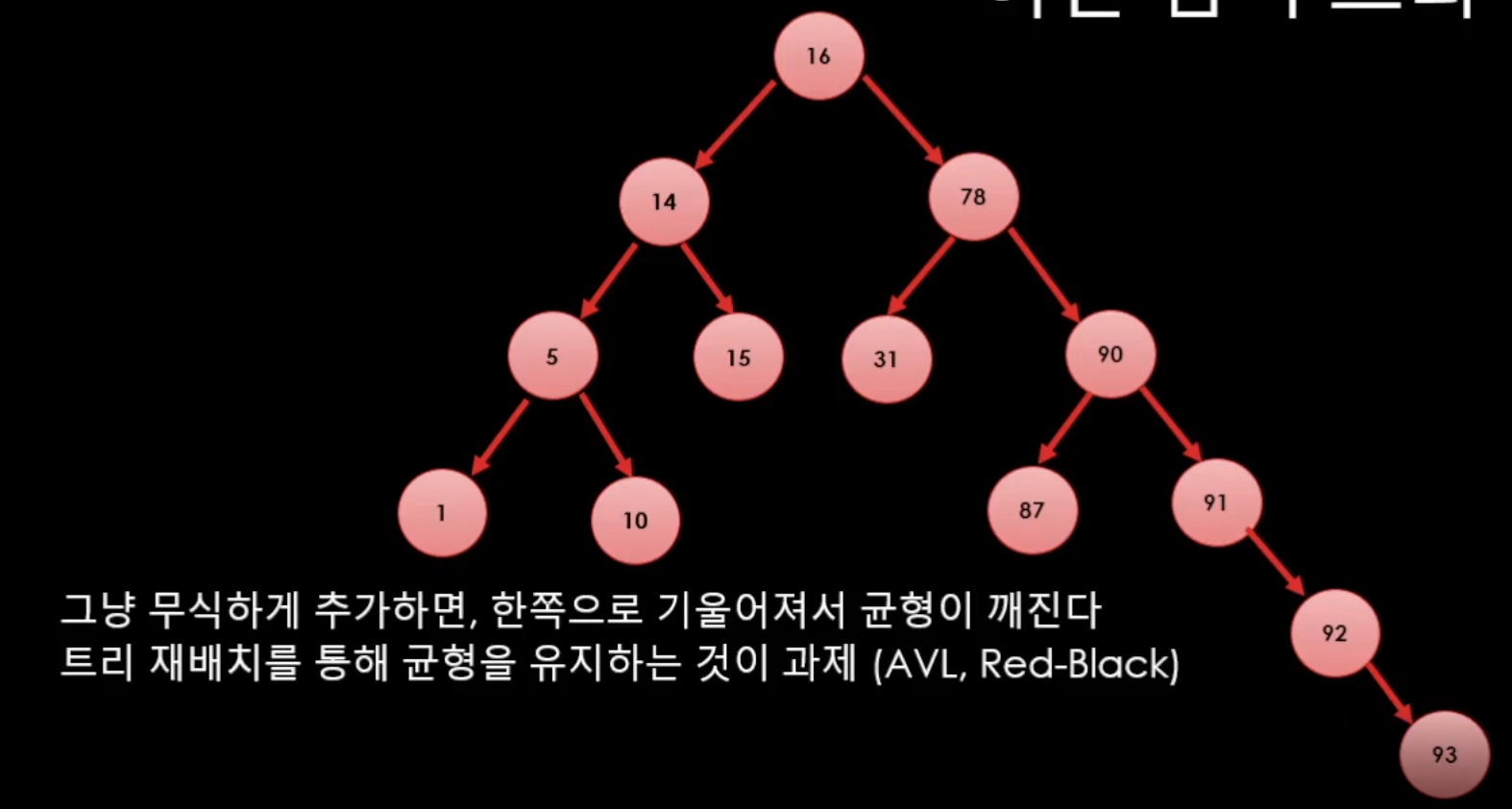
이런식으로 데이터가 늘어나 버린다면 연결 리스트와 다를바가 없어진다.
그래서 트리 재배치를 통해서 균형을 유지하는 것이 과제라고 할 수 있다.

그럼 이제 대충 이진 트리가 무엇인지 알았으니 힙트리에 대해 알아보자.

힙 트리

힙 트리를 공부할 때는 두 가지만 알고있으면 된다.

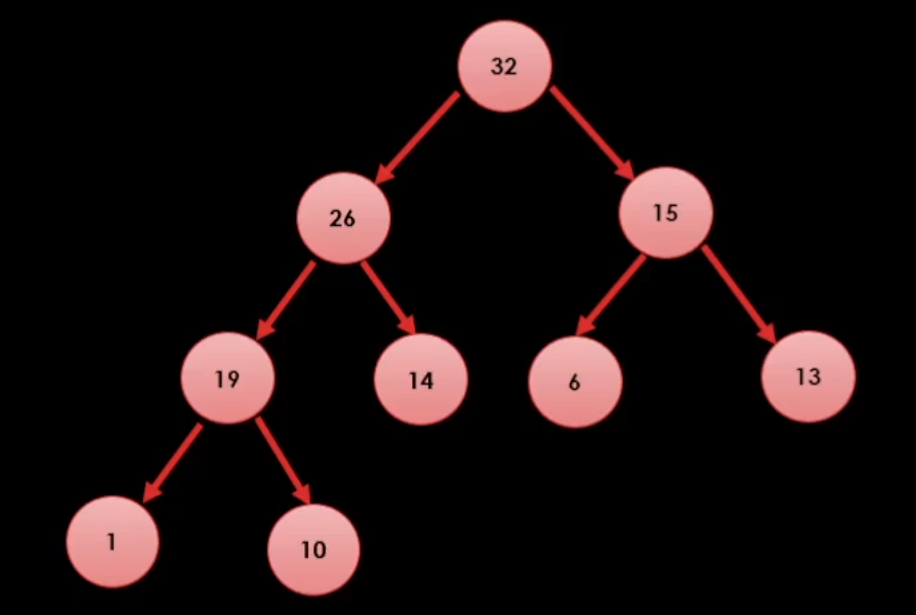
힙 트리 1법칙 : [부모 노드]가 가진 값을 항상 [자식 노드]가 가진 값보다 크다.
(최소값을 구할 때는 반대로 하면 된다.)
(그리고 형제 노드끼리의 조건은 없다. 부모 노드와 자식 노드에 한해서 적용)

그리고
힙 트리에서 데이터를 추가 하고 제거할 때 이런식으로 해야한다.

마지막 레벨을 제외한 모든 레벨에 노드가 꽉 차 있다. (완전 이진 트리)
마지막 레벨에 노드가 있을 때는 ,항상 왼쪽부터 순서대로 채워야 한다.

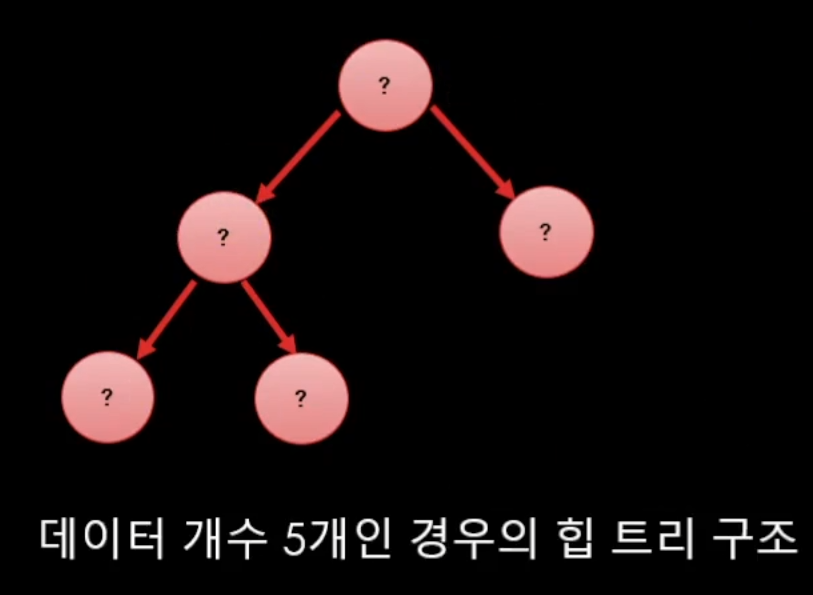
힙 트리 2법칙 : 노드 개수를 알면, 트리 구조는 무조건 확정할 수 있다.

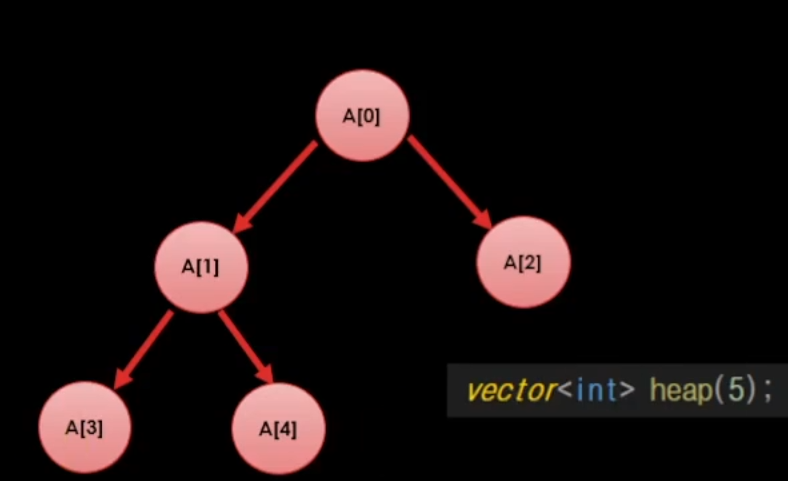
힙 트리를 뭐 Left, Right를 사용하여서 구현할 수도 있지만
바로 vector<int> children(5)이런식으로 배열을 이용해서 힙 구조를 표현할 수 있다.

i번 노드의 왼쪽 자식은 [(2 * i) + 1]번
i번 노드의 오른쪽 자식은 [(2 * i)) + 2] 번
i번 노드의 부모는 [(i - 1) / 2] 번
이라는 공식을 부여할 수 있다.

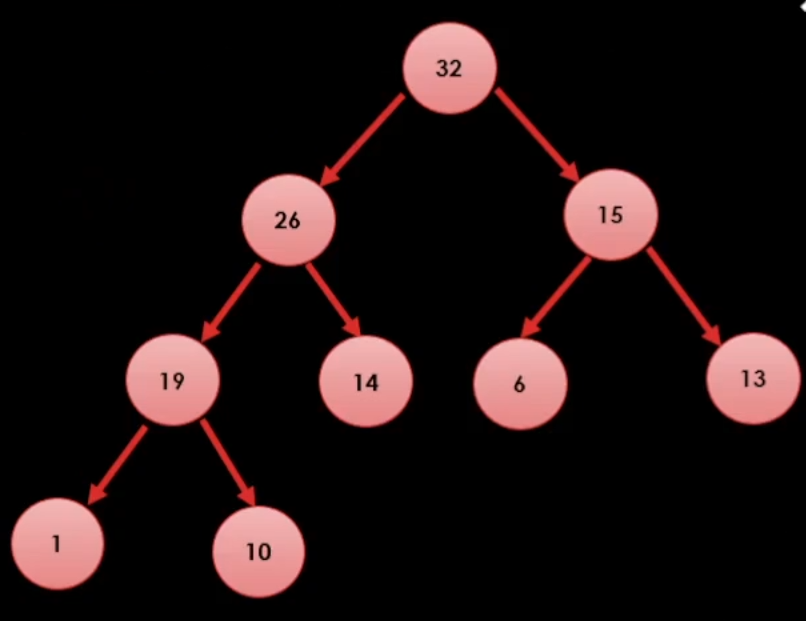
그럼 예제로 31이라는 값을 추가 해보자.

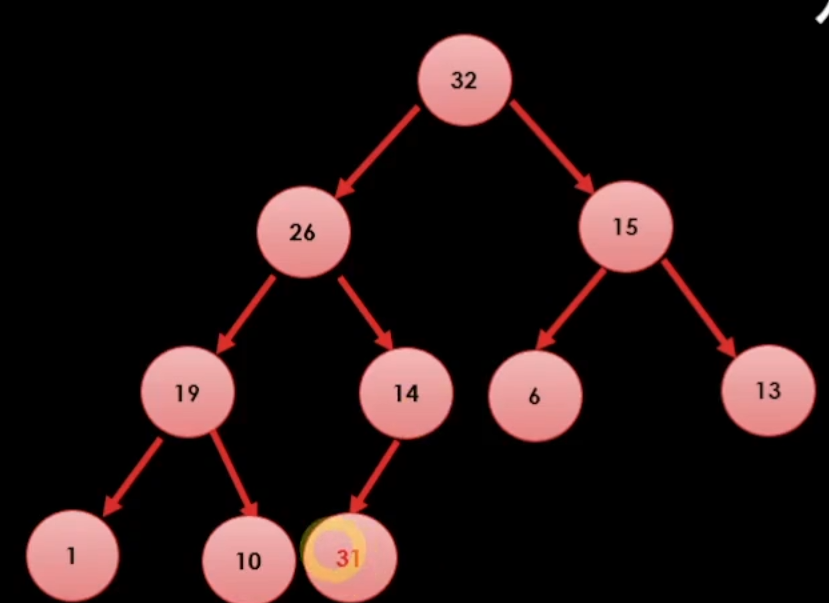
일단 힙 트리 2법칙에 의해서 트리의 구조를 맞춰준다.

그리고 우리는 힙 트리 1법칙을 지키기 위해서 부모 노드와 도장 깨기를 한다.

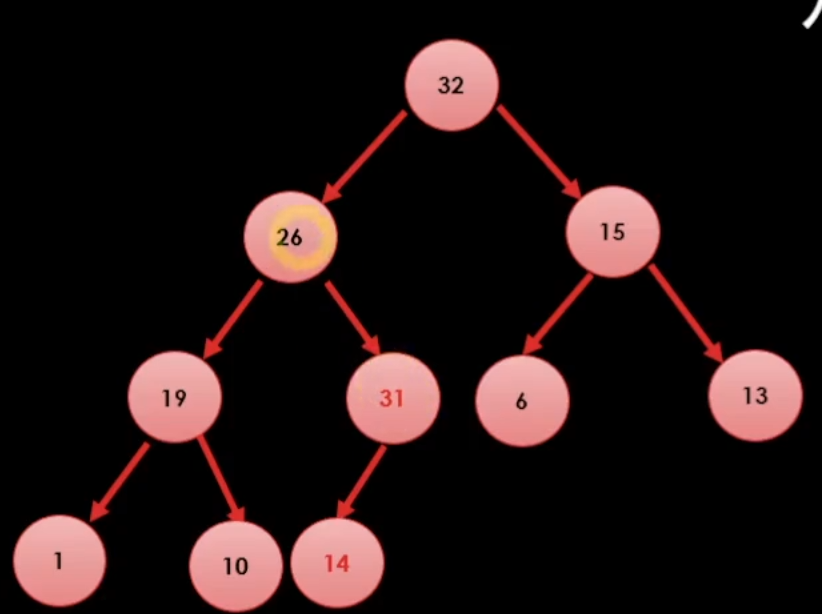
이런식으로 14와 31을 비교하여 31이 더 크다면 둘을 바꾼다.

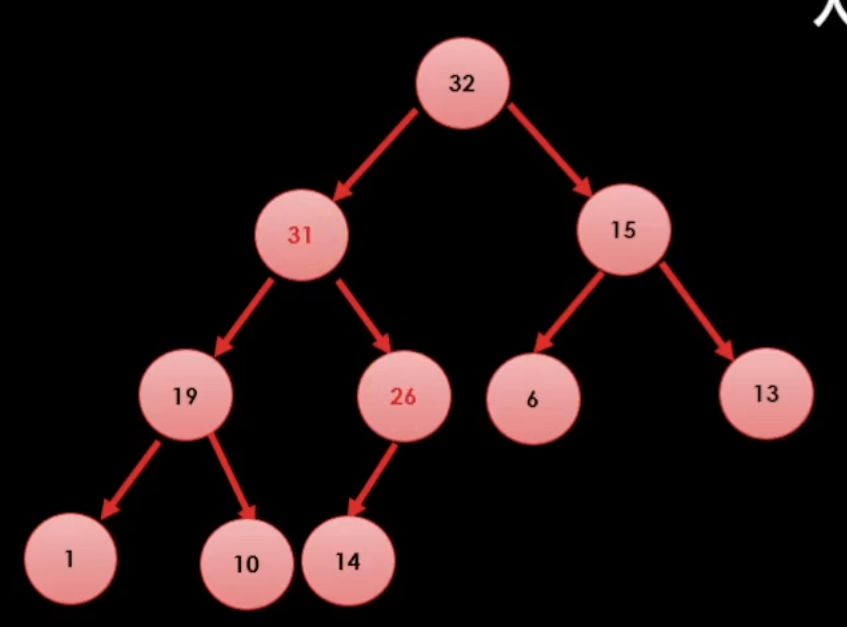
그리고 26과 31을 비교하여 31이 더 크다면 둘을 바꾼다.

이런식으로 값이 추가하는 과정을 알 수 있다.

그럼 최대값을 어떻게 꺼낼까?(pop)

일단 힙 트리 특성상 최대값은 무조건 루트 노드에 있는 값이기 때문에
일단 32를 꺼내준다.

이런식으로 최대값을 먼저 제거해준다.

이러면 힙 트리 2법칙 때문에 제일 마지막에 위치한 데이터를 루트로 옮긴다.

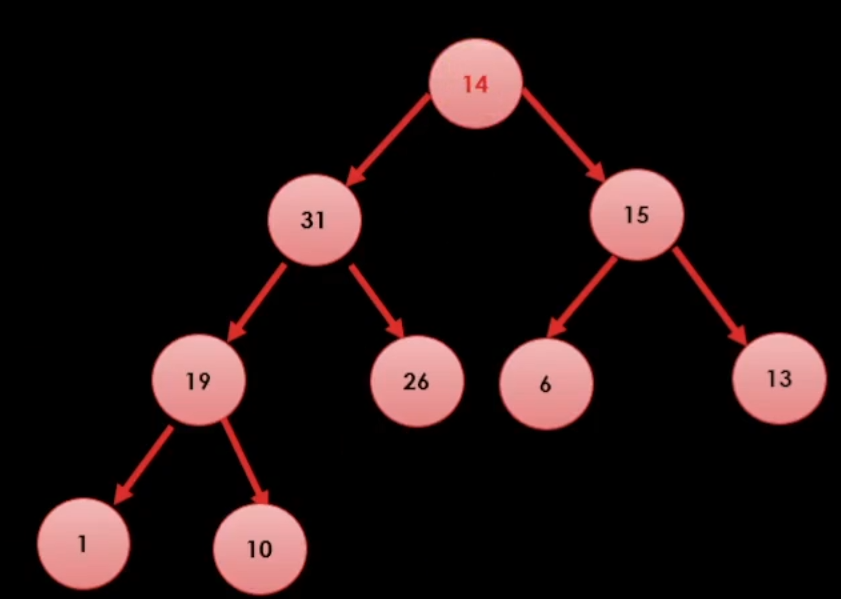
올라간 값이 최대값이 아니면 역 도장 깨기를 해서 자진으로 내려간다.

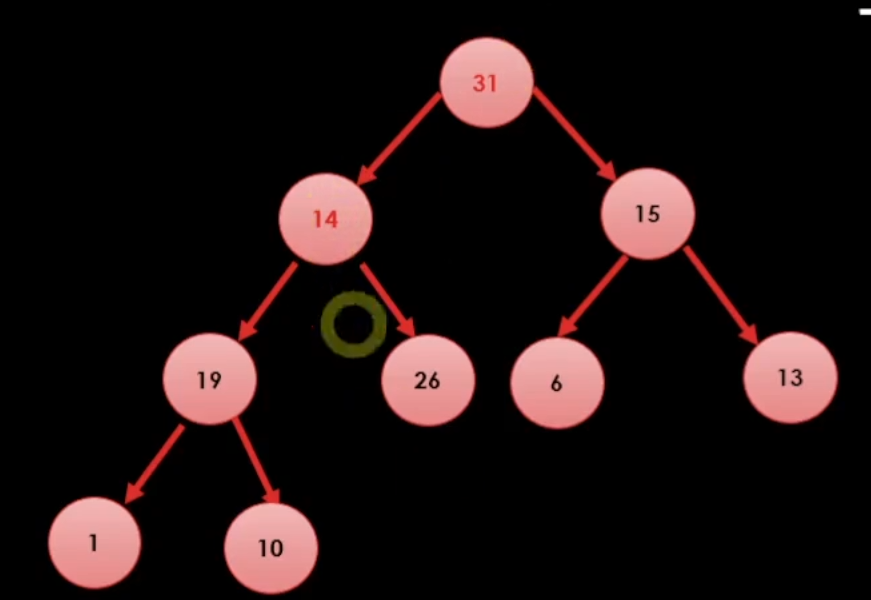
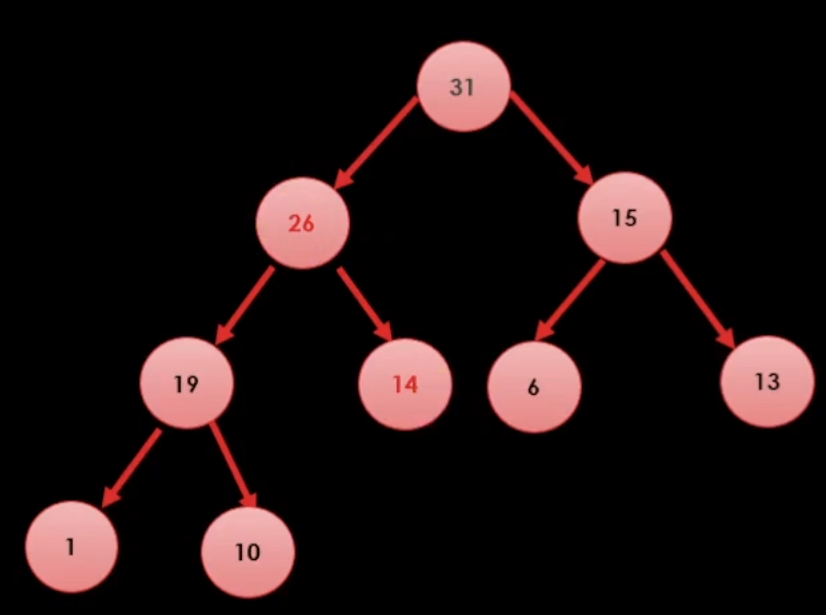
이런식으로 하면 끝이 난다.

결국 최대값을 꺼낼 때에는 최대값을 꺼내주고 노드를 재배치 시켜주면 된다.

구현

구현은 위에 배웠던 것 처럼 만들면 된다.

#include <iostream>
using namespace std;
#include <vector>
#include <queue>

template<typename T, typename Predicate = less<T>>
class PriorityQueue
{
public:
	// O(logN)
	void push(const T& data)
	{
		// 우선 힙 구조부터 맞춰준다
		_heap.push_back(data);

		// 도장깨기 시작
		int now = static_cast<int>(_heap.size()) - 1;

		// 루트 노드까지
		while (now > 0)
		{
			// 부모 노드와 비교해서 더 작으면 패배
			int next = (now - 1) / 2;
			
			//if (_heap[now] < _heap[next])
			//break;
			if (_predicate(_heap[now], _heap[next]))
				break;

			// 데이터 교체
			::swap(_heap[now], _heap[next]);
			now = next;
		}
	}

	// O(logN)
	void pop()
	{
		_heap[0] = _heap.back();
		_heap.pop_back();

		int now = 0;

		while (true)
		{
			int left = 2 * now + 1;
			int right = 2 * now + 2;

			// 리프에 도달한 경우
			if (left >= (int)_heap.size())
				break;

			int next = now;

			// 왼쪽 비교
			if (_heap[next] < _heap[left])
				next = left;

			// 둘 중 승자를 오른쪽과 비교
			//if (right < _heap.size() && _heap[next] < _heap[right])
			if (right < _heap.size() && _predicate(_heap[next], _heap[right]))
				next = right;

			// 왼쪽/오른쪽 둘 다 현재 값보다 작으면 종료
			if (next == now)
				break;

			::swap(_heap[now], _heap[next]);
			now = next;
		}
	}

	// O(1)
	T& top()
	{
		return _heap[0];
	}

	// O(1)
	bool empty()
	{
		return _heap.empty();
	}

private:
	vector<T> _heap;
	Predicate _predicate;
};

이런식으로 위에 배웠던 것과 동일하게 구현하면 된다.

사용은 이런식으로 할 수 있다.

priority_queue<int> pq;

pq.push(10);
pq.push(40);
pq.push(30);
pq.push(50);
pq.push(20);

int value = pq.top();
pq.pop();

만약 최소값을 찾고 싶다면
이런식으로 꼼수? 라고 해야하는지는 모르겠지만 쉽게 바꿔서 사용할 수 있다.

priority_queue<int> pq;

pq.push(-10);
pq.push(-40);
pq.push(-30);
pq.push(-50);
pq.push(-20);

int value = -pq.top();
pq.pop();

다 마이너스로 바꾸고 받을 때 -로 연산하여 가져오면 최소값을 가져올 수 있다.

하지만 이게 싫다면
위에 의문이 들었던 부분 Predicate이 부분을 사용하면 된다.
Predicate로 판별해주는 변수를 만들어 사용할 수 있다.
priority_queue<int, less<int>> pq;
를 사용하면 최대값

priority_queue<int, greater<int>> pq;
를 사용하면 최소값을 얻을 수 있다.

그리고 실제 우선순위 큐는 인자가 하나 더 있다.

이렇게 _Container도 넣어줄 수 있다.(vector)로 넣어주면 된다.

하지만 인자가 기억나지 않다면 처음 방법을 사용하면 된다.

시간 복잡도

트리 특성상 노드가 2배씩 늘어나기 때문에 높이가 늘어나는 것이 느리고
우리가 검색을 할 때 절반만 탐색하기 때문에 우선순위 큐의 시간 복잡도는
O(logN)이라고 볼 수 있다.

설명할 때는 노드 맨 아래에서 타고타고 올라가는 것으로 설명하면 된다.
노드가 1개면 2^1 - 1 높이가 1
노드가 3개면 2^2 - 1 높이가 2
노드가 7개면 2^3 - 1 높이가 3
즉 2의 지수가 트리의 높이이다
그러므로 노드가 N개 일때 높이는 logN이다.