리뷰에 앞서...
드디어 Transformer가 CV에 등장했던 ViT가 엄청난 성과를 이루었다. 하지만 ViT 리뷰에서도 많은 과제가 남아있다고 언급 했었다. 바로 ViT를 Detection이나 Segmentation과 같은 다른 CV 작업에 적용하는 것! 바로 그 과제를 해결한게 이 Swin Transformer라고 생각한다.
나아가 범용 backbone의 역할을 할 수 있도록 Transformer의 적용 가능성을 확장하려고 한 Swin Transformer를 보며 언어 영역 뿐만 아니라 CV에서도 Transformer의 무궁무진한 발전 가능성에 대해서 알 수 있었던 논문이었다.
해당 논문: https://arxiv.org/abs/2103.14030
Official Github: https://github.com/microsoft/Swin-Transformer
Abstract
Computer vision의 범용적인 Backbone 역할을 할 수 있는 Swin Transformer를 제시한다.
Shifted Window를 사용하여 계산되는 hierarchical transformer를 제안한다. Shifted windowing 방식은 self-attention 계산을 겹치지 않는 local window로 제한하는 동시에 cross-window 연결도 허용함으로써 더 큰 효율성을 제공한다.
hierarchical architecture는 다양한 규모로 모델링할 수 있는 유연성을 갖고 있고 이미지 크기와 관련하여 linear computational complexity를 가지고 있다.
Introduction
CNN은 강력한 도구였고 다양한 Vision tasks를 위해 네트워크의 backbone으로 제공되었다. NLP에서 네트워크 구조가 진화하면서 Transformer가 등장했고 이는 Computer vision에도 영향을 미쳤다.
이 논문에서는 Computer vision을 위한 범용 backbone 역할을 할 수 있도록 Transformer의 적용 가능성을 확장하려고 한다.
Language Transformers에서 사용되는 단어 토큰과 달리 시각적 요소는 scale이 크게 다를 수 있고 이는 Object detection과 같은 작업에서 문제로 여겨진다. 기존 Transformer 기반 모델에서 토큰은 모두 고정된 규모여서 vision에는 적합하지 않은 속성이다. 또 다른 차이점은 텍스트 구절의 단어에 비해 이미지의 픽셀 해상도가 훨씬 높다. 픽셀 수준에서 조밀한 예측이 필요한 Sementatic segmentation과 같은 작업은 self-attention의 계산 복잡성이 이미지 크기에 비례하므로 고해상도 이미지에서는 Transformer가 이를 처리가 어렵다.
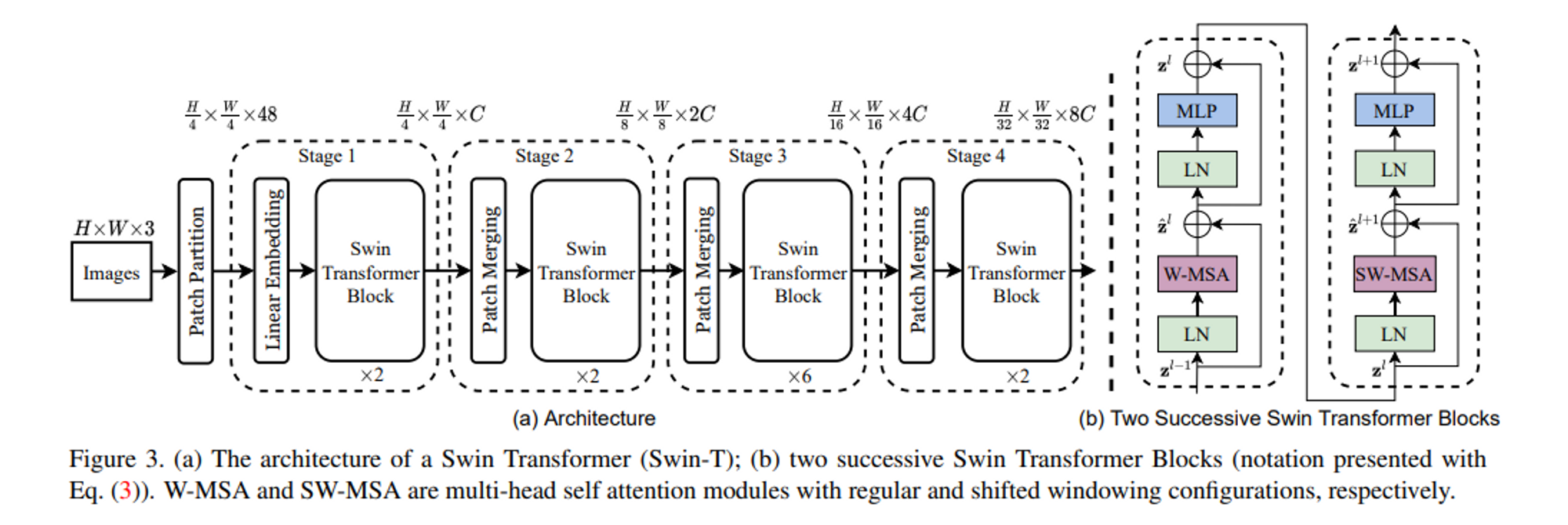
이러한 문제를 극복하기 위해 hierarchical feature maps을 구성하고 이미지 크기에 linear computational complexity를 갖는 Swin Transforemr라는 범용 Transforemr Backbone을 제안한다.
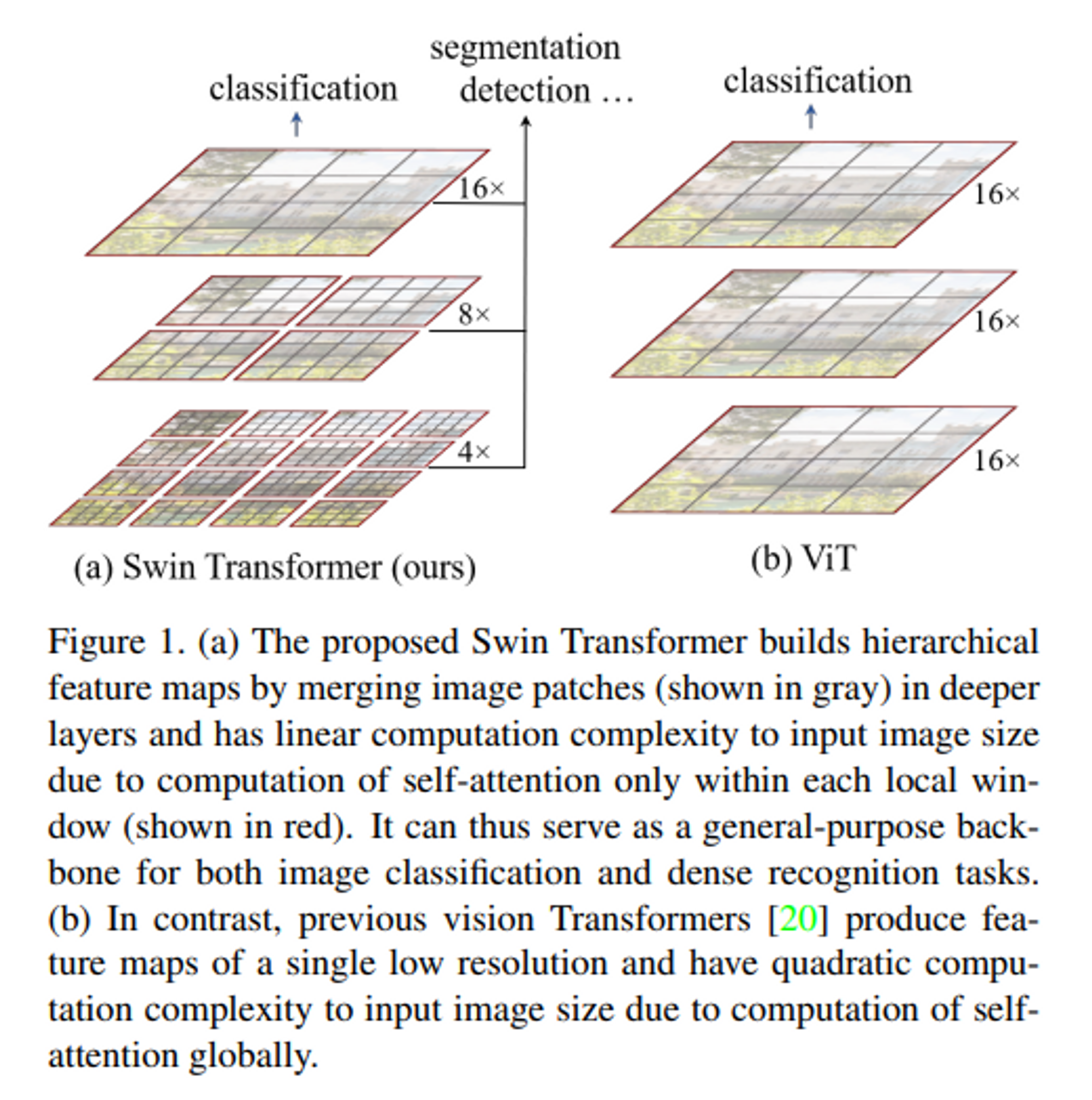
Linear computational complexity는 이미지를 겹치지 않게 분할하는 window(빨간색 윤곽선) 내에서 Local self-attention을 계산하여 달성한다. 각 패치 수는 고정되어 있으므로 복잡성을 이미지 크기에 비례하게 된다. 이러한 장점을 통해 backbone으로 활용되기 적합하다.
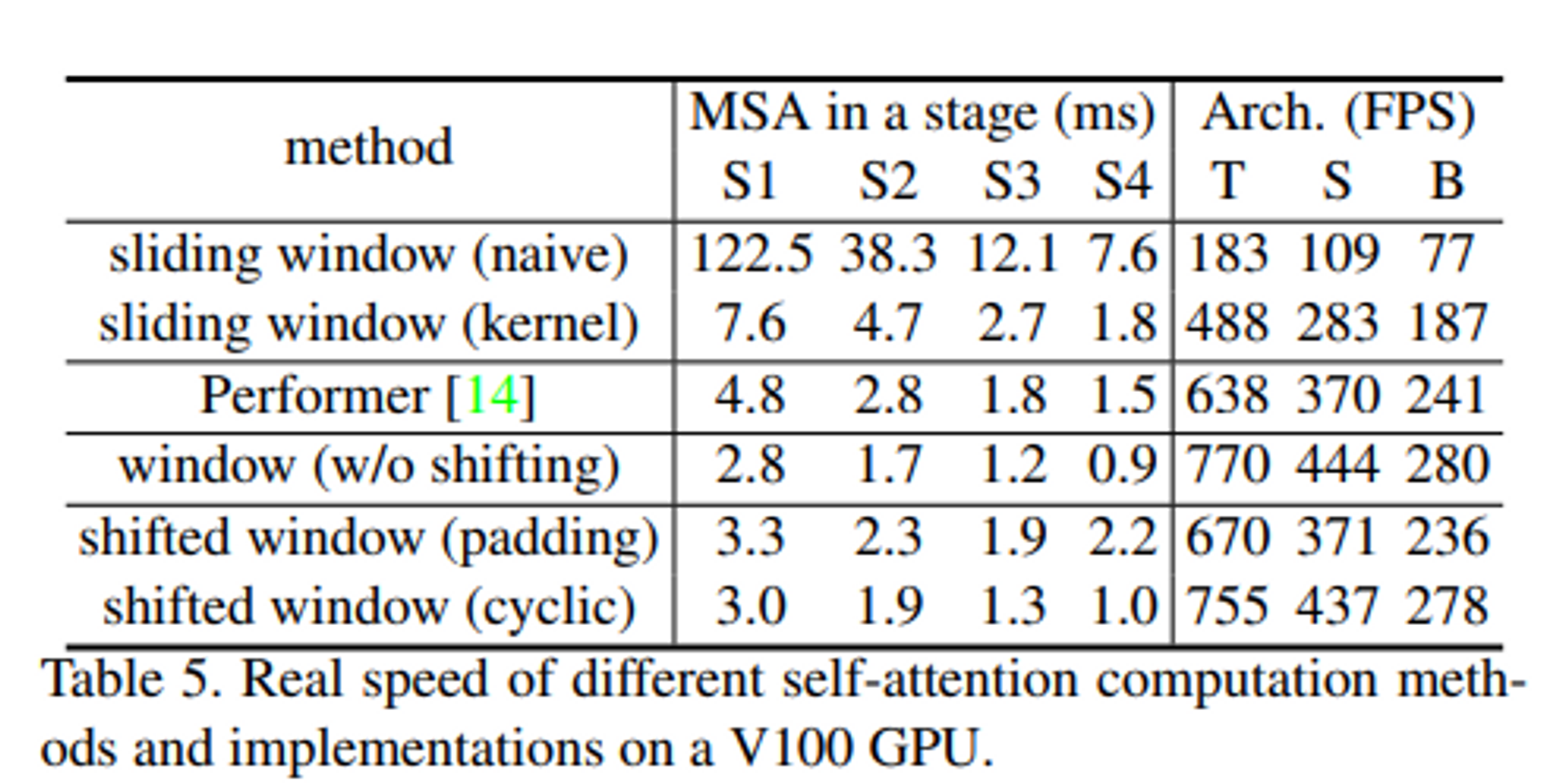
Method
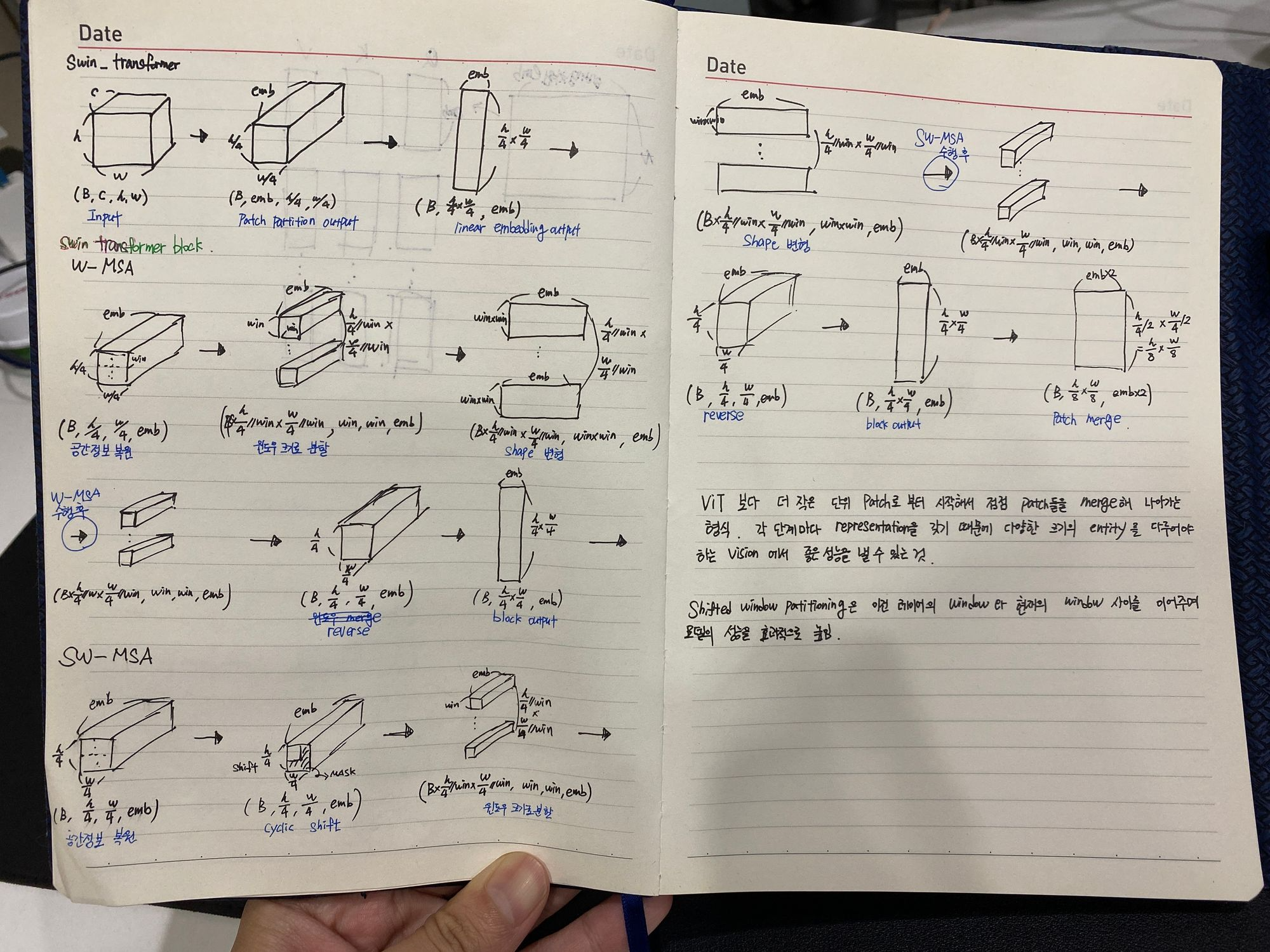
stage 1에서는 Linear Embedding과 Swin Transformer 블록이 존재한다. stage 1의 output 형태는 input 형태와 같다.
stage 2에서는 hierarchical 표현을 생성하기 위해 패치 병합 레이어에 의해 토큰 수가 갑소한다. 즉, 서로 이웃한 패치들을 연결하고(Patch Merging), Swin Transformer 블록을 지난다. 해상도는 에서 로 변하고 feature dimension은 C에서 2C로 변한다.
stage 3, 4는 stage 2가 두번 반복되는 형태이다.
Swin Transformer Block
Swin Transformer는 표준 multi-head self-attention (MSA) 모듈을 shifted windows 기반 모듈로 교체하고 다른 레이어는 동일하게 유지하여 구축된다. Swin Transformer 블록은 shifted windows 기반 MSA 모듈과 그 사이에 GELU 비선형이 있는 2계층 MLP로 구성되어 있다. LayerNorm(LN) 레이어는 각 MSA 모듈과 각 MLP 이전에 적용되고 residual connection은 각 모듈 이후에 적용된다.
Shifted Window based Self-Attention
Self-attention in non-overlapped windows
local windows 내에서 self-attention을 계산하는 것을 제안한다. 만약, 각 windows에 M x M 패치들이 포함되어 있다고 가정하면, 계산 복잡성은 다음과 같다.
전자는 패치에 대해 quadrtic하게 증가하고 후자는 M이 고정될 때 linear하게 증가한다.
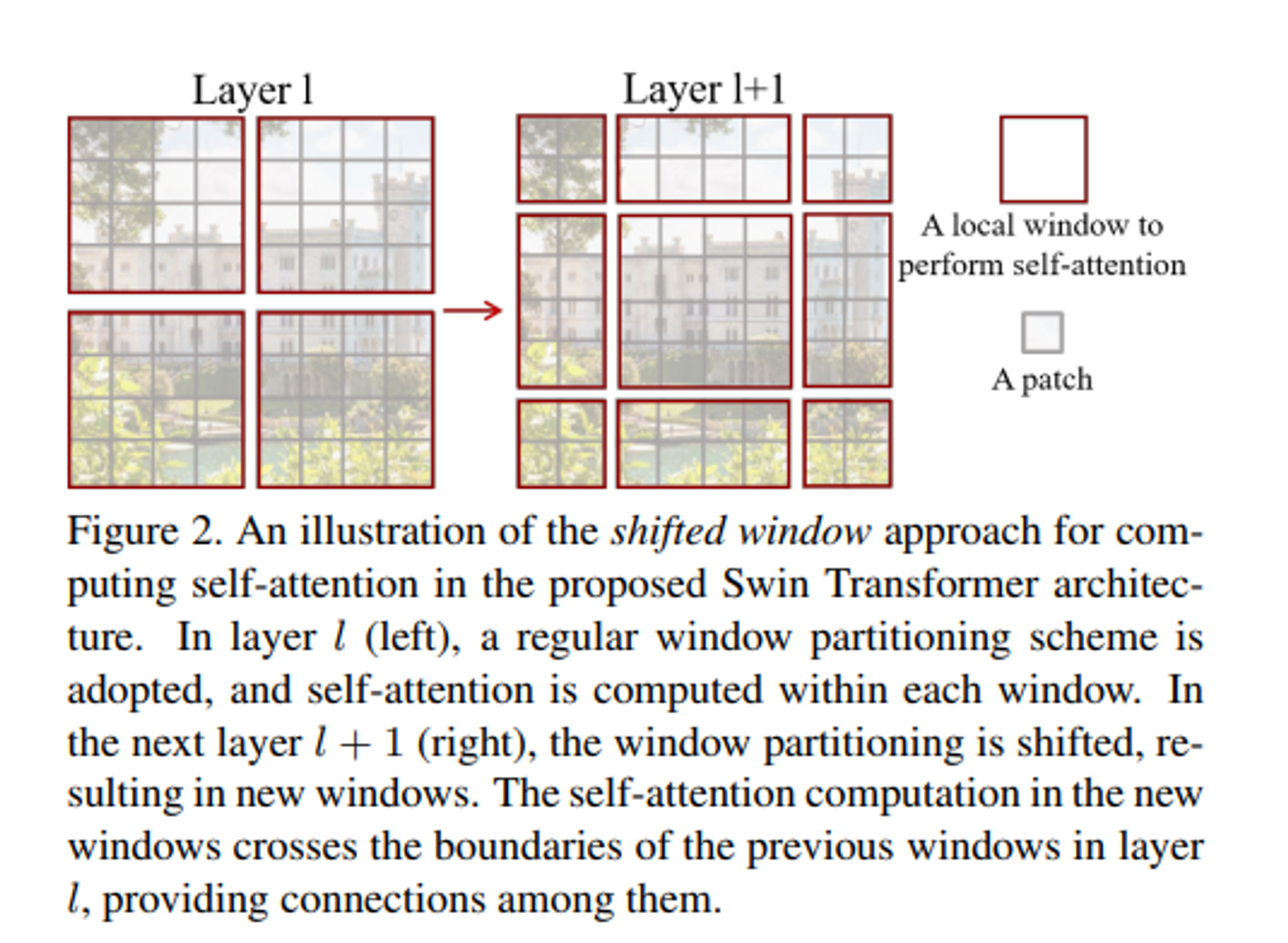
Shifted window partitioning in sucessive blocks
window-based self-attention 모듈은 window 간의 연결이 부족하여 모델링 능력이 제한된다. 겹치지 않는 windows의 효율적인 계산을 유지하면서 windows간의 연결을 도입하기 위해 Shifted window partitioning 접근 방식을 제안한다.
하지만 가장 중요한 것은 효율적으로 window를 배치해야하는 것이다.
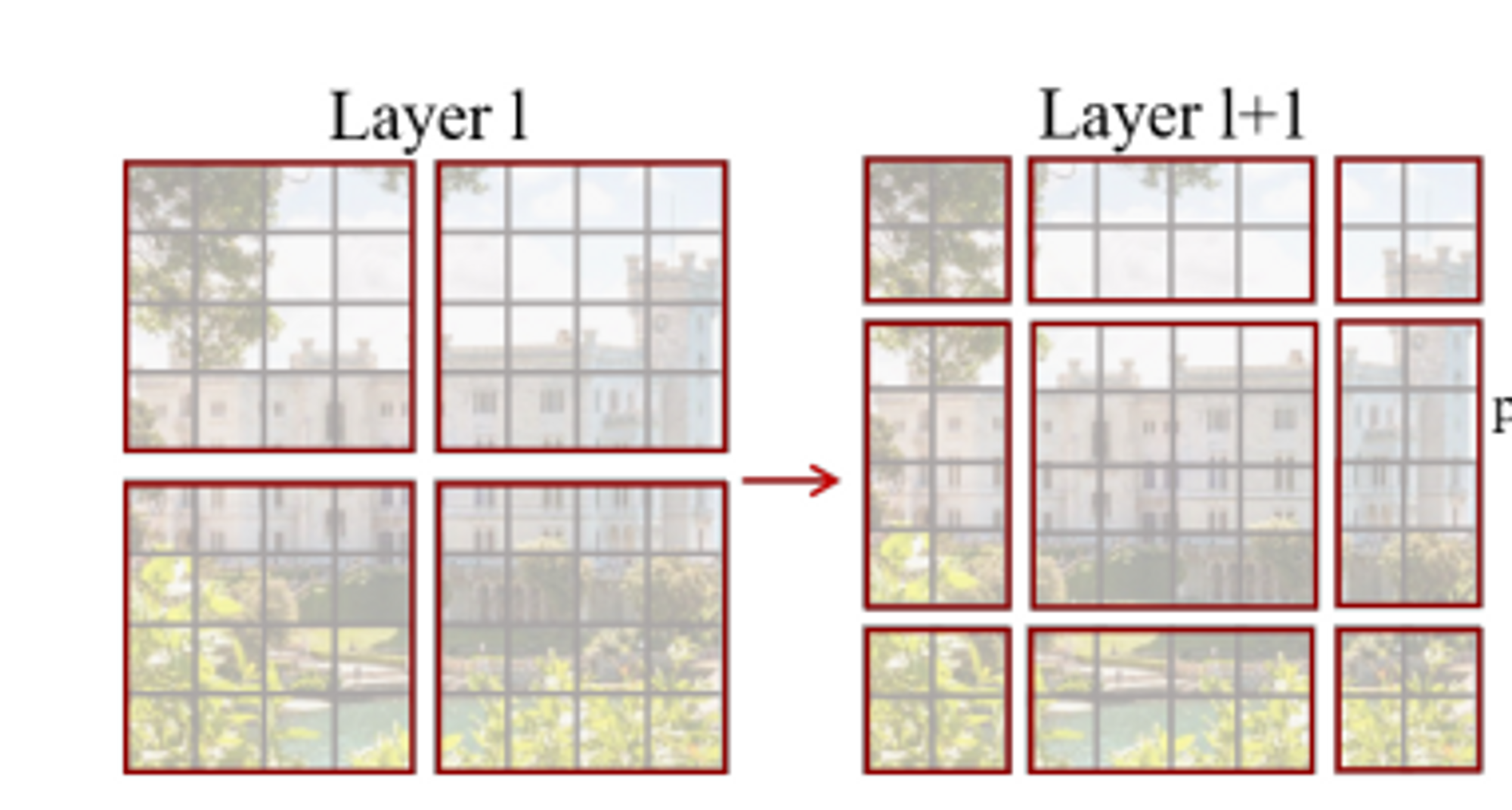
위 그림처럼 W-MSA에서 였던 window 수가 SW-MSA 모듈에서는 로 달라지게 될 뿐만 아니라 M x M 보다 작은 window들도 있기 때문이다.
따라서 논문에서는 두 가지 approach를 제안한다.
-
naive solution
작아진 window들에 padding을 두어 크기를 다시 M x M으로 맞추고, attention을 계산할 때 padding된 값들을 마스킹 해준다. 하지만 window수는 여전히 늘어나게 되기 때문에 computation은 상당하다. -
cyclic-shifting toward the top-left direction
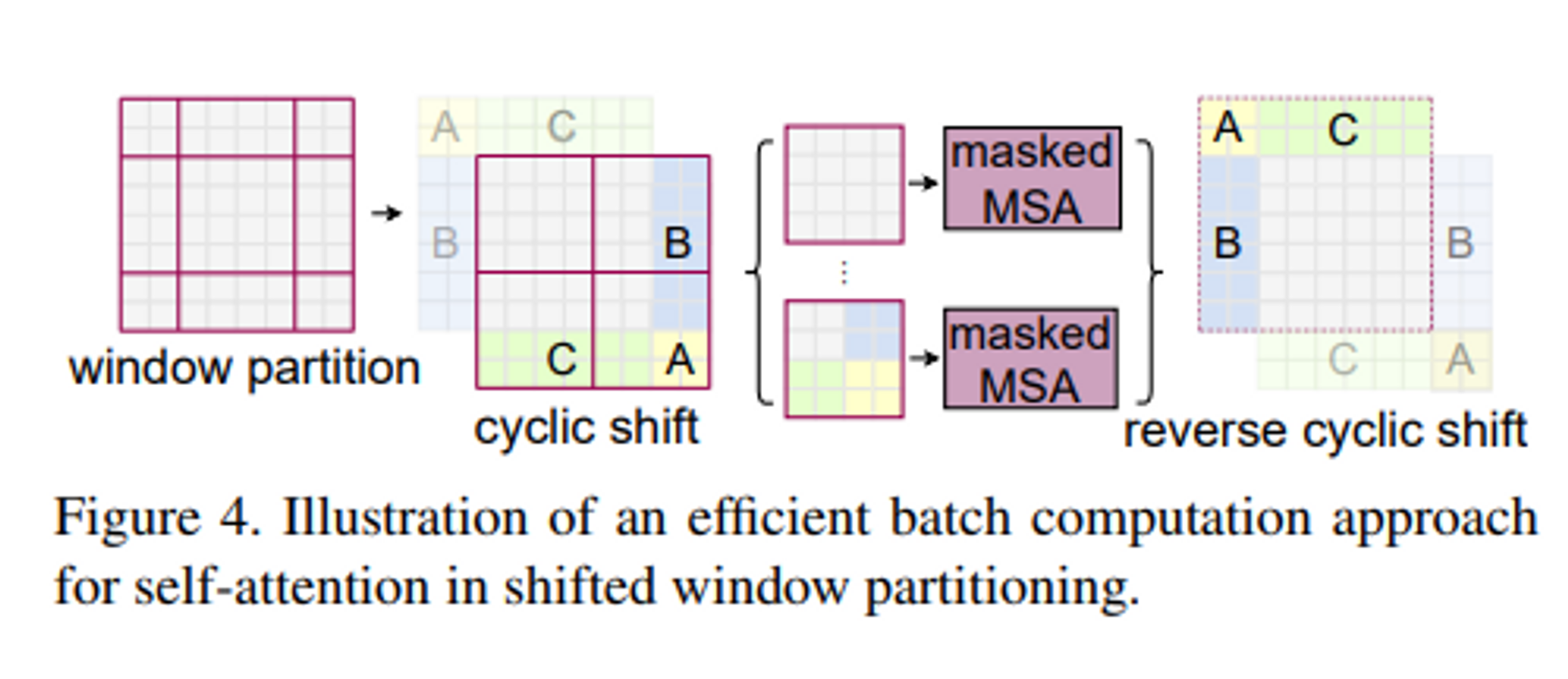
왼쪽 상단을 향해 cyclic하게 회전한다. shift 이후 window는 feature map에서 인접하지 않은 여러 하위 windows로 구성될 수 있으므로 self-attention 계산을 각 sub-windows 내로 제한하기 위해 마스킹 메커니즘이 사용된다.
 cyclice shift 예시
cyclice shift 예시
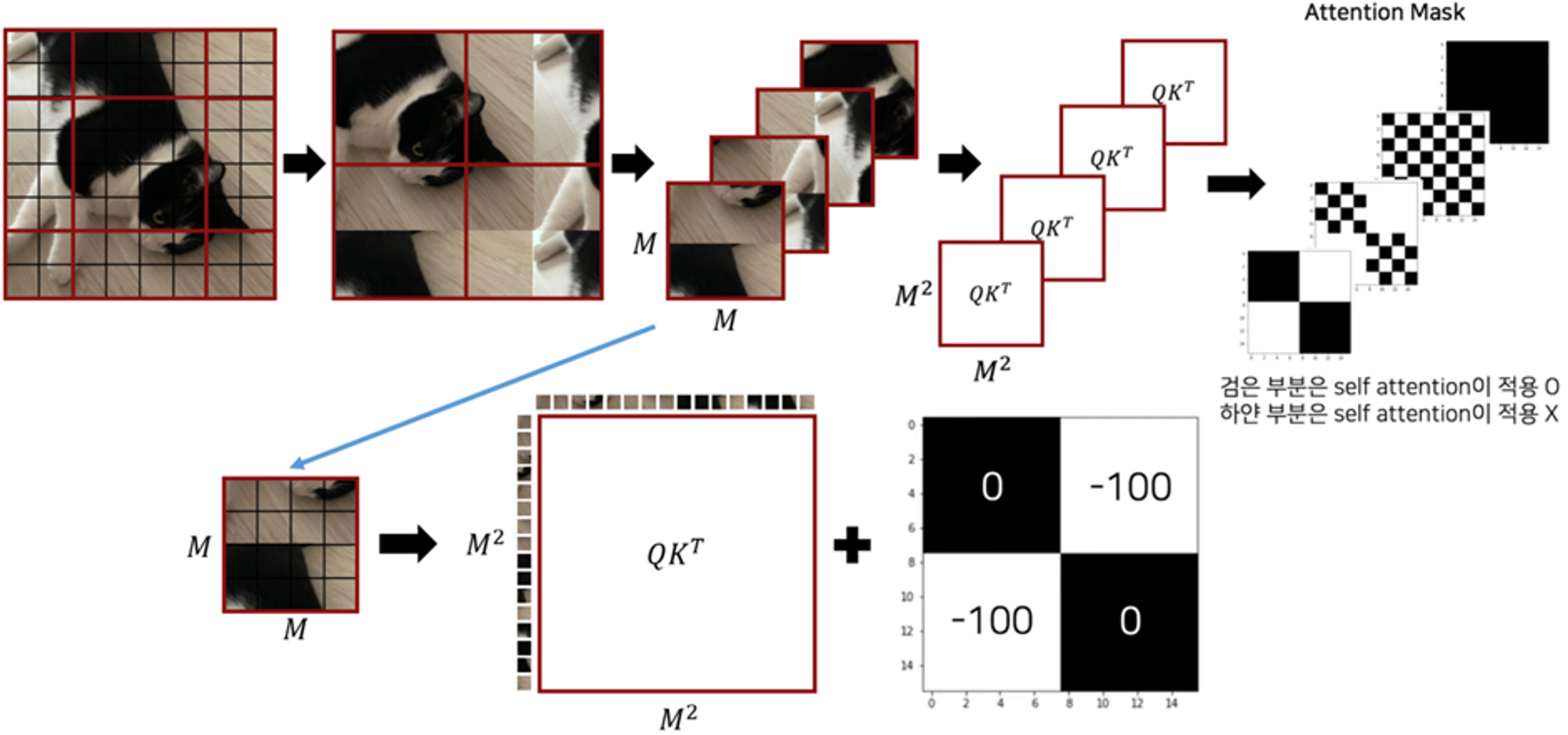 cyclic shift와 MSA
cyclic shift와 MSA
Relative position bias
Swin Transformer는 self-attention을 수행하는 과정에서 relative position bias를 추가해준다.
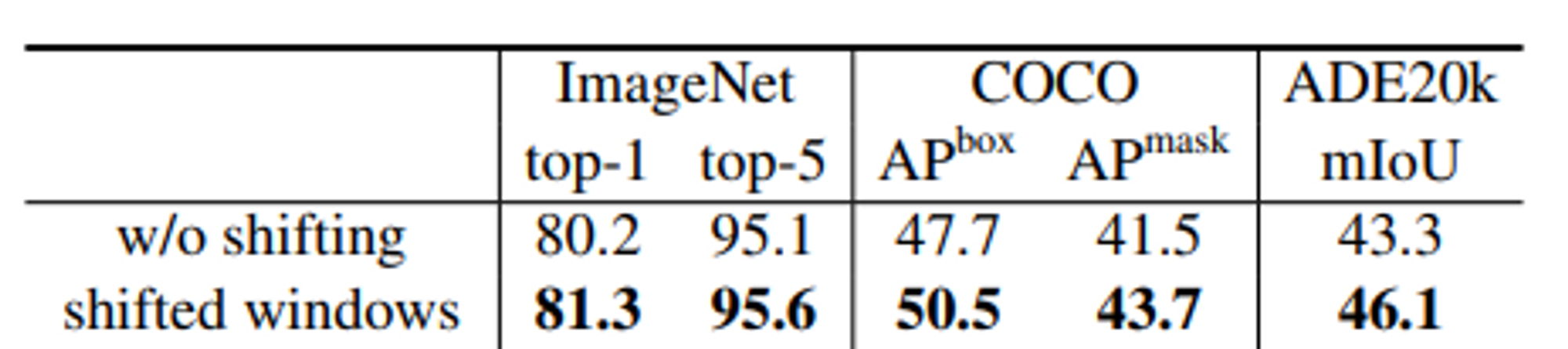
기존 position embedding이 절대좌표를 더해주는 식 이었던 것에 반해 위치는 상대적이라는 개념을 적용한 relative position representation이라고 할 수 있다. 기존 absolute position embedding을 사용했을 때보다 상당한 모델 성능 향상을 보였다고 한다.
아래 그림은 Swin Transformer의 tensor 변화에 대한 그림이다.