정말 정말 힘들었다..
최대한 이해한 부분이라도 써보겠다 (기억상실을 방지하기 위함)

Intro

low bitwidth quantization or model pruning은 억만개의 파라미터에 대해 비용이 많이 드는 retraining을 요구한다.

때문에! 재훈련이 없는 one shot인 post-training method(PTQ)가 굉장히 매력적으로 느껴질 것이다.
불행히도, 이러한 변형은 억만개의 파라미터 스케일로 확장하기 어렵다..

본 논문에서는 GPTQ라는 새로운 학습 후 양자화 방법을 제시하는데, 이 방법은 최대 몇 시간 안에 수천억 개의 매개 변수가 있는 모델에서 실행할 수 있을 정도로 효율적이며 정확도의 큰 손실 없이 이러한 모델을 매개 변수당 3비트 또는 4비트로 압축할 수 있을 정도로 정밀하다.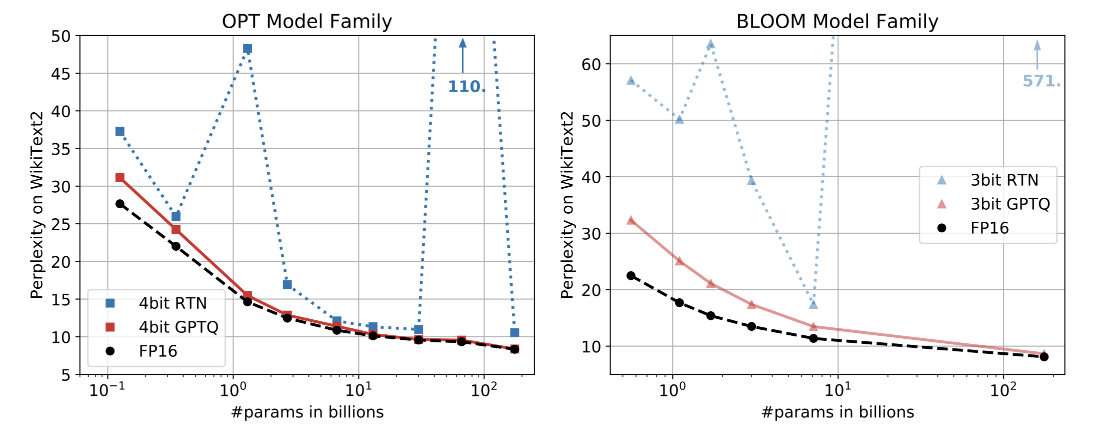

GPTQ는 수천 억 개의 매개 변수를 가진 매우 정확한 언어 모델이 3-4 비트/성분으로 양자화될 수 있다는 것을 처음으로 보여주었다!

Background

layer-wise quantization

layer-wise quantization은 말 그대로 레이어 별로 퀀타이제이션을 하는 것을 의미한다.
시각적으로 쉽게 나타내자면

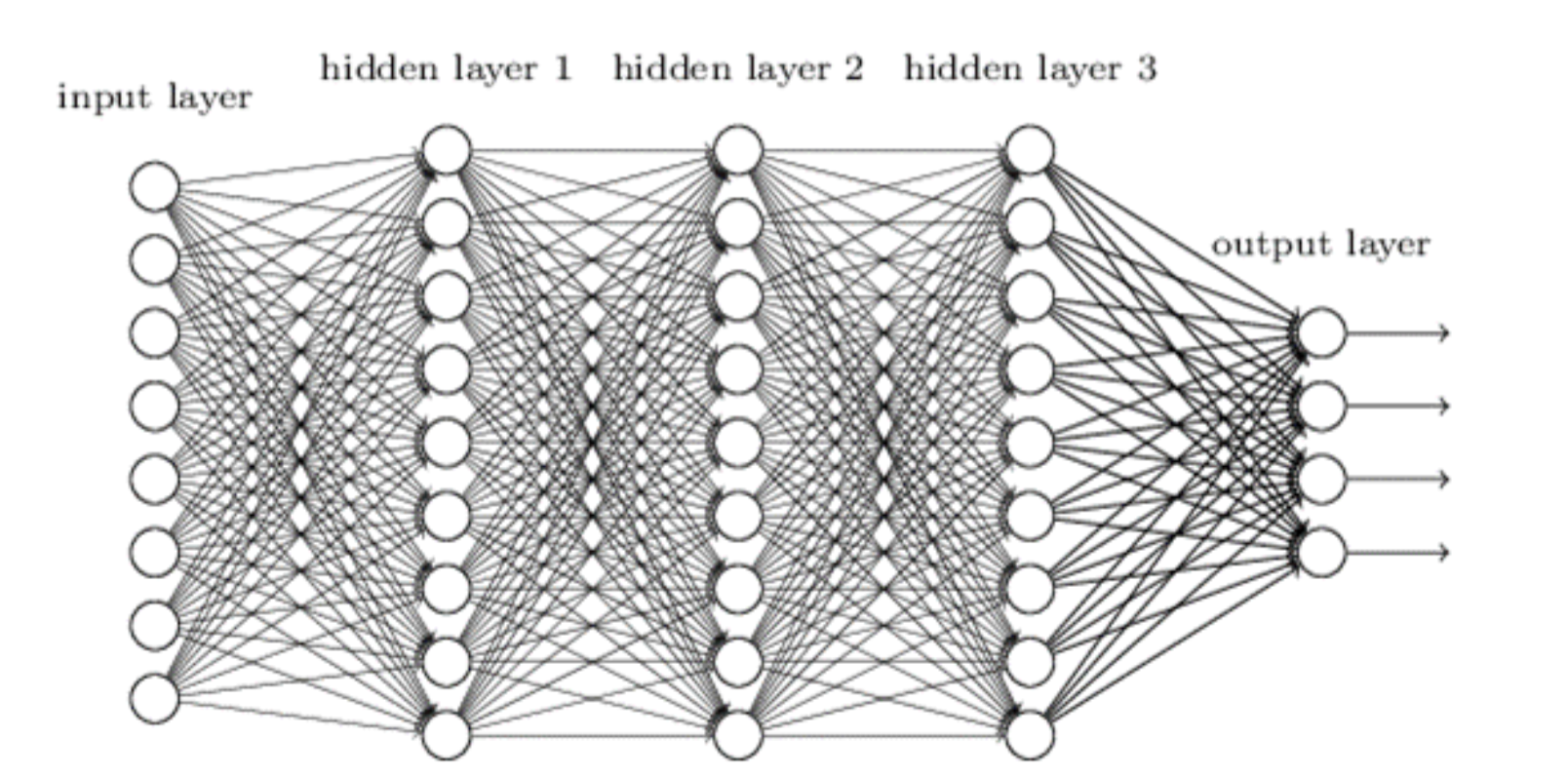
이렇게 여러 개의 layer들 별로 양자화 해주겠다는 것이다.

Concretely, let Wℓ be the weights corresponding to a linear layer ℓ and let Xℓ denote the layer input corresponding to a small set of m data points running through the network.

쉽게 그림을 통해서 이해해보자.
그림에 hidden layer1, 2, 3이 있는데 이를 Wℓ(ℓ=1,2,3)으로 볼 수 있을 것이다. 그리고 Xℓ은 ℓ번째 레이어의 입력으로 한다. (이 부분이 아리까리)
그리고 quantization된 weight matrix를 W̃라고 하자.

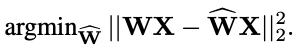
원래의 WX와 W̃X를 최소화하는 W̃를 찾는것이 목표다. 즉! quantize하면서 원래의 결과를 훼손하지 않는 것!

Optimal Brain Quantization(OBQ)

OBQ를 알기 위해선 먼저 OBS, hessian matrix를 알아야 한다.

hessian matrix : https://velog.io/@nochesita/%EC%B5%9C%EC%A0%81%ED%99%94%EC%9D%B4%EB%A1%A0-%ED%97%A4%EC%8B%9C%EC%95%88-%ED%96%89%EB%A0%AC-Hessian-Metrix

OBS :

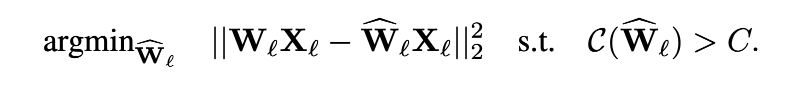
layerwise quatization을 위해서 구해놓은 식을 loss function이라고 하고,
이를 hessian matrix의 함수로 쓴다.

W̃에 대해서 2번 미분하게 되며, 이를 H라고 표시한다.
역 헤세 행렬은 함수의 최소값이나 최대값을 찾기 위한 반복적 방법인 뉴턴 방법이나 준뉴턴 방법과 같은 최적화 알고리즘에 사용된다.

따라서 다음과 같은 식이 나오게 된다.

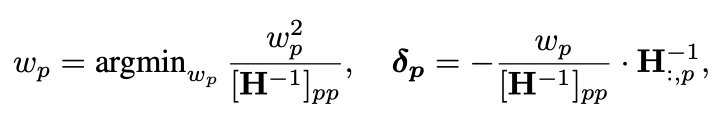
wp는 손실을 최소화하는 가중치, δp은 프루닝을 하고 나서의 나머지 가중치 업데이트이다.

---

퀀타이제이션을 취하면 아래와 같은 식을 받아낼 수 있다.

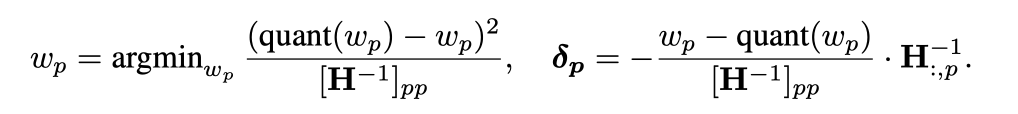
wp를 제거하고 난 후, H 역행렬은 다음과 같은 식으로 update할 수 있다.

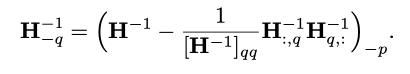
H역행렬 -q : 행q, 열q를 제거한 H 역행렬

The GPTQ Algorithm

Step1: Arbitrary Order Insight

OBQ는 W의 row를 독립적으로 퀀타이즈했다. 이는 greedy 한 방식으로 진행되었는데, 예로 들자면 이런 것이다.

A B C D
E F G H
I J K L
M N O P

이런 식으로 4*4 배열이 있다고 가정하자. 그럼 OBQ는 각 행마다 가장 손실함수를 최소화하는 것을 뽑는다.
그러면 A, F, L, O가 뽑힐 것이다.

그런데 GPTQ에서 제시하는 것은 Greedy하게 뽑을 필요가 없다는 것이다!
크고 매개변수가 많은 레이어에서 가중치를 양자화할할 때 임의 순서로 해도 비슷한 성능을 낼 수 있다는 것을 발견했다.
따라서 정말 임의의 순서를 정하고 row별로 뽑아본다. (to quantize the weights of all rows in the same order)
예를 들자면, 그냥 행의 첫번째 요소들을 뽑는다고 하고 A, E, I, M을 뽑는 것이다.

그러면 HF 역행렬을 dcol 번의 반복만으로 업데이트 할 수 있다!

Step2: Lazy Batch-Updates

먼저, 이 알고리즘은 메모리 접근 대비 계산 속도가 낮아서 실제로 빠르게 실행되지 않을 수 있다는 문제가 일어난다. 특히, H 역행렬 업데이트와 같은 연산은 행렬의 모든 요소를 업데이트해야 하며 각 항목마다 몇 개의 부동 소수점 연산(FLOP)만 필요로 한다. 이러한 연산은 현대 GPU의 강력한 계산 능력을 제대로 활용할 수 없으며, 메모리 대역폭이 상당히 낮아서 병목 현상을 초래한다.

열(column)에 대한 최종 반올림 결정이 해당 열에서 수행된 업데이트에만 영향을 미친다. 따라서 특정 열의 업데이트는 해당 열과 그에 해당하는 H^-1 행렬의 부분에만 영향을 미치며, 다른 열들에는 영향을 미치지 않는다.

영향을 미치지 않기 때문에 먼저 B=128로 범위를 잡고 해당 범위에 대하여 quant와 가중치 업데이트를 진행한다.

그 뒤 남은 가중치에 대해서 업데이트를 진행한다.

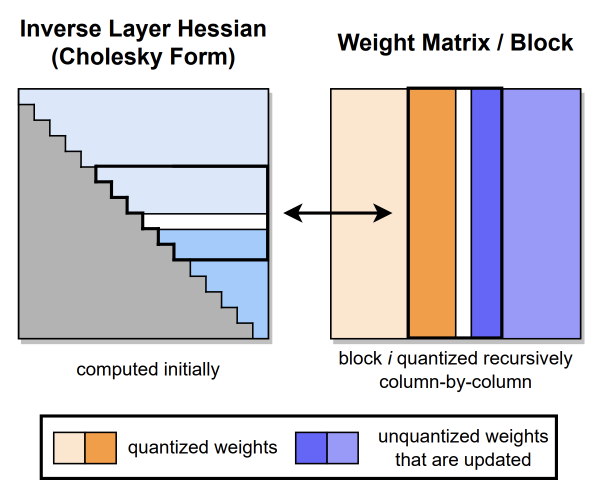
Step3 : Cholesky Reformulation

대규모 모델에서는 수치적인 불안정성이 큰 문제가 될 수 있다. 특히 이전 단계에서 설명한 블록 업데이트와 결합될 경우 더 큰 문제가 발생할 수 있다.

특히, 이는 헤세 행렬의 역행렬이 indefinite할 때 발생할 수 있다!
이때 헤세 행렬의 역행렬(HF-1)을 안정적으로 계산할 수 있게 하는 것이 cholesky인 것이다.

"block quantization errors"는 가중치 행렬을 블록 단위로 양자화할 때 발생하는 오차를 나타낸다. 이 부분은 양자화된 블록의 가중치와 원래 가중치 간의 차이를 계산하여 나타내고 있다.