5.0. 오차역전파법(Backpropagation)

1. 수치 미분은 계산 시간이 오래 걸림 -> 오차역전파법으로 가중치 매개변수의 기울기 계산 대체
2. = ‘역전파법’, ‘역전파’

5.1. 계산 그래프(computational graph)

1. 계산과정을 그래프로 나타낸 것.

2. 순전파(forward propagation) : 왼쪽에서 오른쪽으로 진행. 출발점부터 종착점으로의 전파) ↔ **역전파(backward propagation) : 종착점에서 출발점으로의 전파

3. 국소적 계산을 전파하여 최종 결과를 얻음. 전체 계산의 복잡도와 관계 없이, 각 관계에서 하는 일은 해당 노드의 국소적 계산.

4. 계산 그래프 활용의 이점
   1) 전체 연산 복잡도와 관계 없이 각 노드에서 단순한 계산에 집중하여 문제 단순화
   2) 중간 계산 결과 보관 가능
   3) 역전파를 통해 미분을 효율적으로 계산할 수 있음

5.2. 연쇄법칙(chain rule)

1. 계산 그래프의 역전파
   

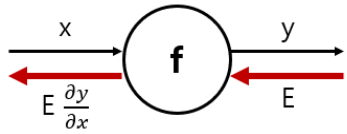
2. 역전파 계산 : 상류에서 전달된 값인 신호 E에 국소적 미분을 곱한 후, 다음 노드로 전달

3. 국소적 미분을 전달하는 원리는 연쇄법칙에 따름

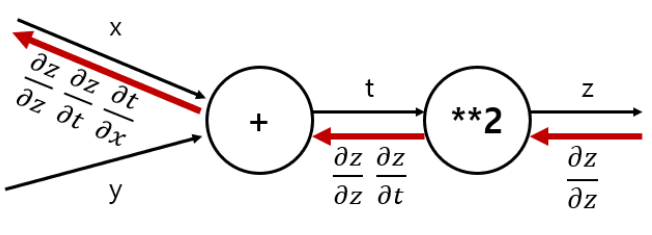
4. 연쇄 법칙은 합성함수의 미분에 대한 성질임. 하단 그림의 맨 왼쪽 노드에서 는 서로 약분 하면 x에 대한 z의 미분이 되어, 역전파가 하는 일은 연쇄 법칙의 원리와 동일
   

5.3. 역전파

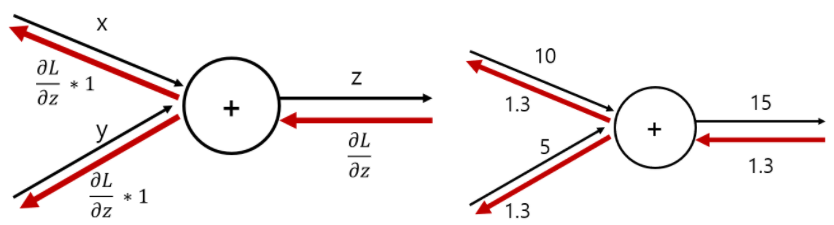
1. 덧셈 노드의 역전파 : 입력 신호를 다음 노드로 출력할 뿐
   

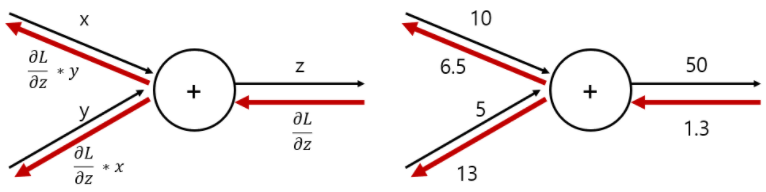
2. 곱셈 노드의 역전파
   1) 상류값에 순전파 때의 입력신호들을 서로 바꾼 값을 곱해 하류로 보냄
   2) 덧셈에서와는 달리, 순방향 입력신호의 값이 필요함 -> 순전파의 입력신호를 변수에 저장해둬야 함
   

5.4. 단순한 계층(노드 단위) 구현

덧셈 및 곱셈 노드의 역전파 코드 구현은 하단 링크 참조

5.5. 활성화 함수 계층 구현

1. 신경망을 구성하는 층(계층)을 각각 하나의 클래스로 구현

2. ReLU 계층 : 순전파 입력인 x가 0보다 크면 역전파는 상류 값을 그대로 하류로 흘림. 0이하이면 하류로 신호 보내지 않음(0보냄) (소스 코드는 하단 링크 참조)
   

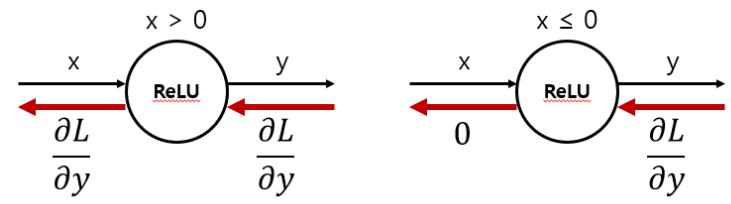
3. Sigmoid 계층 : 시그모이드 계층의 역전파는 순전파의 출력(y)만으로 계산 가능 (소스 코드는 하단 링크 참조)
   

5.6. Affine/Softmax 계층 구현

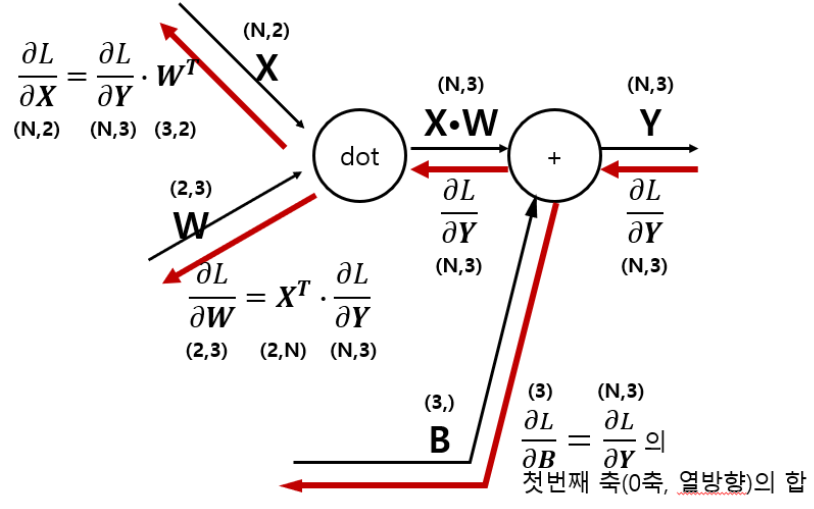
1. Affine 계층
   1) 어파인 변환(Affine transformation) : 신경망의 순전파 시 수행하는 행렬의 곱을 기하학에서 부르는 말

2. 배치용 Affine 계층 : 데이터 N개를 묶어 순전파하는 경우(소스 코드는 하단 링크 참조)
   

3. Softmax-with-Loss 계층
   1) 소프트맥스 함수는 입력값을 정규화하여 출력
   2) 소프트맥스 계층과 손실함수인 교차 엔트로피 오차를 포함해 Softmax-with-Loss라 명명
   3) 입력 이미지가 Affine 계층과 ReLU 계층을 통과하며 변환
   4) 마지막 Softmax 계층은 입력(a1, a2, a3)을 정규화해 (y1, y2, y3)를 받고, 이 데이터로부터 손실 L을 출력
   
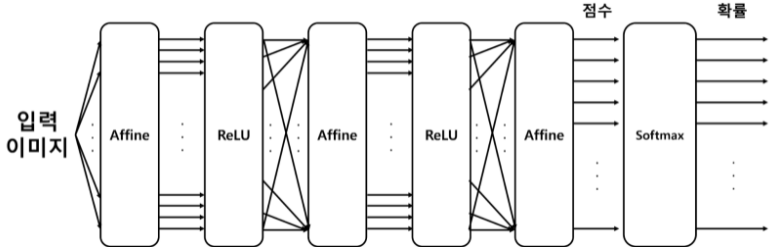
   5) 3개 클래스로 분류한다 가정했을 시 아래와 같은 계층 구조를 가짐
   
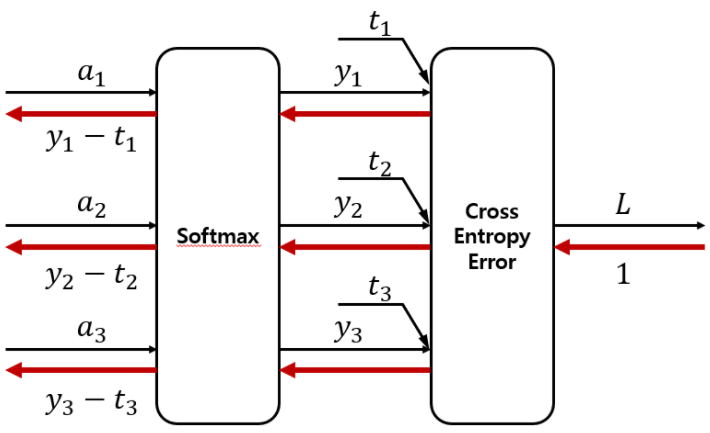
   6) Softmax함수의 손실함수로 교차 엔트로피 오차를 사용하여 역전파가 (y1-t1, y2-t2, y3-t3)로 'Softmax계층 출력-정답 레이블의 차분'으로 말끔히 떨어져 앞 계층에 전해짐(소스 코드는 하단 링크 참조)

5.7. 오차역전파법 구하기

해당 절의 모든 소스코드는 하단 링크 참조

1. 오차역전파법을 적용한 2층 신경망 구현
2. 오차역전파법으로 구한 기울기 검증
   1) 기울기 확인(gradient check) : 수치미분과 오차역전파법으로 구한 기울기가 거의 같은지(일치하는지) 검증하는 작업
   2) 수치미분은 느리나, 오차역전파법의 정확성을 확인하기 위해 필요
3. 오차역전파법을 사용한 학습 구현

참조 링크

밑바닥부터 시작하는 딥러닝 5장 예제 소스 링크