💡k-평균 클러스터링(k-means clustering)

• 주어진 데이터를 k개(number of centroids)의 cluster로 묶는 알고리즘이다.
  각 cluster는 하나의 중심(centroid)를 가진다. 각 객체는 가장 가까운 중심에 할당되며, 같은 중심에 할당된 개체들끼리 모여서 하나의 cluster를 형성하는 방식이다.

✍️ k-menas clustering 과정

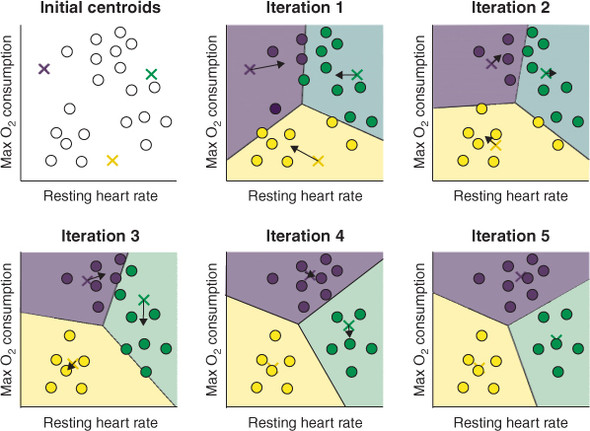
1. k 값을 초기값으로, k 개의 centroid 선정 (아래 그림에서 3개의 x)
2. 각 데이터 포인터를 가장 가까운 centroid에 할당
3. centroid에 할당된 모든 데이터 포인트의 중심 위치 계산 (centroid 재조정)
4. 재조정 된 centroid와 가장 가까운 데이터 포인트 할당

• 이 과정을 cluster에 유의미한 변화가 없을 때까지(optimized 될 때까지) 반복한다.

✍️ k-means 에서 k를 결정하는 방법

1. The Eyeball Method : 사람이 눈으로 보고 판단하여 임의로 지정하는 방법
2. Metrics : 객관적인 지표를 통해 최적화된 k를 선택하는 방법
   Ex)
   Hierarchical Clustering의 시각화 Dendrogram이용,
   The Elbow Method(: scree plot) 이용,
   The Silhouette Method

---

📖 Python 예제

python으로 k-means clustering 실습하기

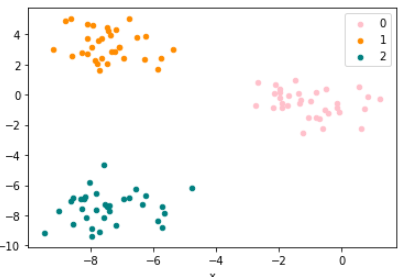
1. 데이터 준비, plot으로 표현

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs

x, y = make_blobs(n_samples = 100, centers = 3, n_features = 2)

# make_blobs 함수?
# 등방성 가우시안 정규분포를 이용해 가상 데이터를 생성하는 함수 
# (보통 클러스링 용 가상데이터를 생성하는데 사용)
'''
parameter
n_samples : 표본 데이터의 수, 디폴트 100
n_features : 독립 변수의 수, 디폴트 20
centers : 생성할 클러스터의 수 혹은 중심, [n_centers, n_features] 크기의 배열. 디폴트 3
cluster_std: 클러스터의 표준 편차, 디폴트 1.0
center_box: 생성할 클러스터의 바운딩 박스(bounding box), 디폴트 (-10.0, 10.0))

return:
X : [n_samples, n_features] 크기의 배열, 독립 변수
    (즉, 데이터 포인터의 위치, cluster가 표현된 것)
y : [n_samples] 크기의 배열, 종속 변수
    (x로 인해 cluster 별로 나누어진 integer 값)
'''

df = pd.DataFrame(dict(dx = x[:, 0], y = x[:, 1], label = y))

colors = {0 : 'pink', 1 : 'darkorange', 2 : 'teal'}
fig, ax = plt.subplots()
grouped = df.groupby('label')

for key, group in grouped:
    group.plot(ax = ax, kind = 'scatter',
    		   x = 'x', y = 'y', label = key, color = colors[key])
plt.show()   

2. label 제거 후 데이터 포인터로 plot 확인

data_points = df.drop('label', axis = 1)

plt.scatter(data_points.x, data_points.y)
plt.show()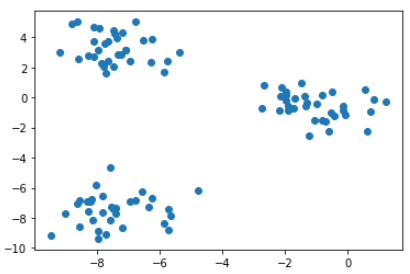

3. 중심점(centroid) 계산

# centroid 계산
dataset_centroid_x = data_points.x.mean()
dataset_centroid_y = data_points.y.mean()

# print(dataset_centroid_x, dataset_centroid_y) 
#    = -0.5316497686409459, -3.8350266662423365

# centroid plot으로 표현
ax.plot(data_points.x, data_points.y)            # (-0.5, -3.8) 표시
ax = plt.subplot()
ax.scatter(data_points.x, data_points.y)
ax.plot(dataset_centroid_x, dataset_centroid_y, "oy")
plt.show()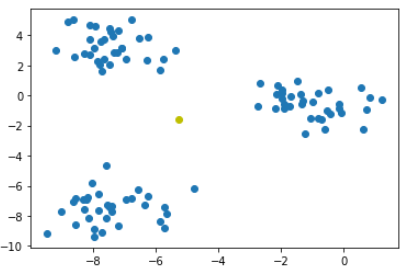

4. random한 point를 가상 cluster의 centroid로 지정

# k-means with 3 cluster. 3개의 sample centroid 설정
centroids = data_points.sample(3)

# plot 표현
ax = plt.subplot()
ax.scatter(data_points.x, data_points.y)
ax.plot(centroids.iloc[0].x, centroids.iloc[0].y, "or")
ax.plot(centroids.iloc[1].x, centroids.iloc[1].y, "oc")
ax.plot(centroids.iloc[2].x, centroids.iloc[2].y, "oy")
plt.show()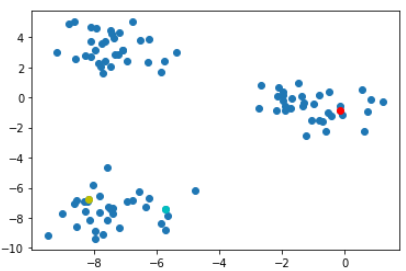

5. centroid 재조정

import math
import numpy as np
from scipy.spatial import distance

def find_nearest_centroid(df, centroids, iteration):
 
  # 포인트와 centroid 간의 거리 계산
  distances = distance.cdist(df, centroids, 'euclidean')
  
  # 제일 근접한 centroid 선택
  nearest_centroids = np.argmin(distances, axis = 1)
    
  # cluster 할당
  se = pd.Series(nearest_centroids)
  df['cluster_' + iteration] = se.values
  
  return df


def plot_clusters(df, column_header, centroids):
  colors = {0 : 'red', 1 : 'cyan', 2 : 'yellow'}
  fig, ax = plt.subplots()
  ax.plot(centroids.iloc[0].x, centroids.iloc[0].y, "ok") # 기존 중심점
  ax.plot(centroids.iloc[1].x, centroids.iloc[1].y, "ok")
  ax.plot(centroids.iloc[2].x, centroids.iloc[2].y, "ok")
  grouped = df.groupby(column_header)
  for key, group in grouped:
      group.plot(ax = ax, kind = 'scatter',
       			 x = 'x', y = 'y', label = key, color = colors[key])
  plt.show()
  

def get_centroids(df, column_header):
  new_centroids = df.groupby(column_header).mean()
  return new_centroids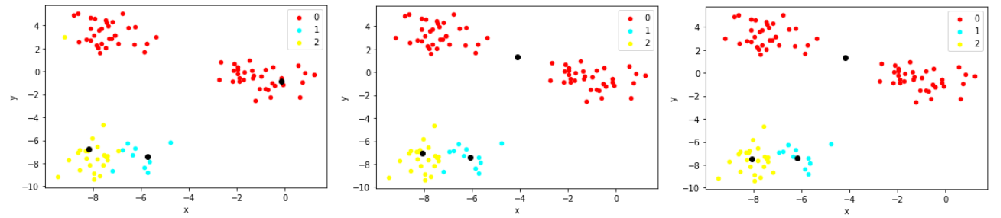

여러번 centroid를 재조정 하면서 유의미한 차이가 없을 때 까지 반복한다.
위 함수를 상세히 다루지 않고 기록만 한 이유는 라이브러리를 통해 구현할 수 있기 때문이다.

k-means with skckit-learn

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans 

# random data 생성
x, y = make_blobs(n_samples = 100, centers = 3, n_features = 2)
df = pd.DataFrame(dict(x = x[:, 0], y = x[:, 1], label = y))

# k-means clustering
kmeans = KMeans(n_clusters = 3)        # k=3 
kmeans.fit(x)                          # clustering 수행
labels = kmeans.predict(x)                # labels 변수 선언


# clustering 결과를 시각화
x = df.iloc[:, 0].values
y = df.iloc[:, 1].values
colors = np.array([0, 10, 20])
plt.scatter(x, y, c=y, alpha=0.5)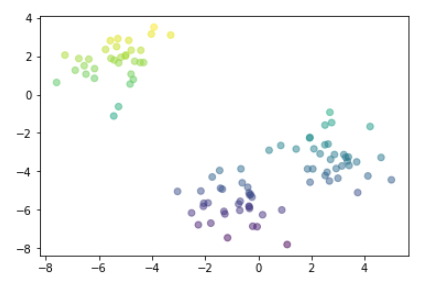

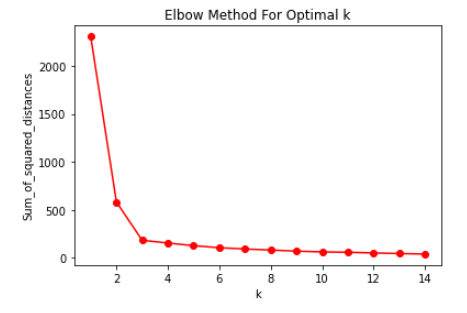
Elbow methods

sum_of_squared_distances = []
K = range(1, 15)
for k in K:
    km = KMeans(n_clusters = k)
    km = km.fit(df)
    sum_of_squared_distances.append(km.inertia_)
   
# 시각화
plt.plot(K, sum_of_squared_distances, 'ro-')
plt.xlabel('k')
plt.ylabel('Sum_of_squared_distances')
plt.title('Elbow Method For Optimal k')
plt.show()

---